一文弄懂神经网络中的反向传播法(Backpropagation algorithm)

最近在看深度学习的东西，一开始看的吴恩达的UFLDL教程，有中文版就直接看了，后来发现有些地方总是不是很明确，又去看英文版，然后又找了些资料看，才发现，中文版的译者在翻译的时候会对省略的公式推导过程进行补充，但是补充的又是错的，难怪觉得有问题。反向传播法其实是神经网络的基础了，但是很多人在学的时候总是会遇到一些问题，或者看到大篇的公式觉得好像很难就退缩了，其实不难，就是一个链式求导法则反复用。如果不想看公式，可以直接把数值带进去，实际的计算一下，体会一下这个过程之后再来推导公式，这样就会觉得很容易了。

说到神经网络，大家看到这个图应该不陌生：

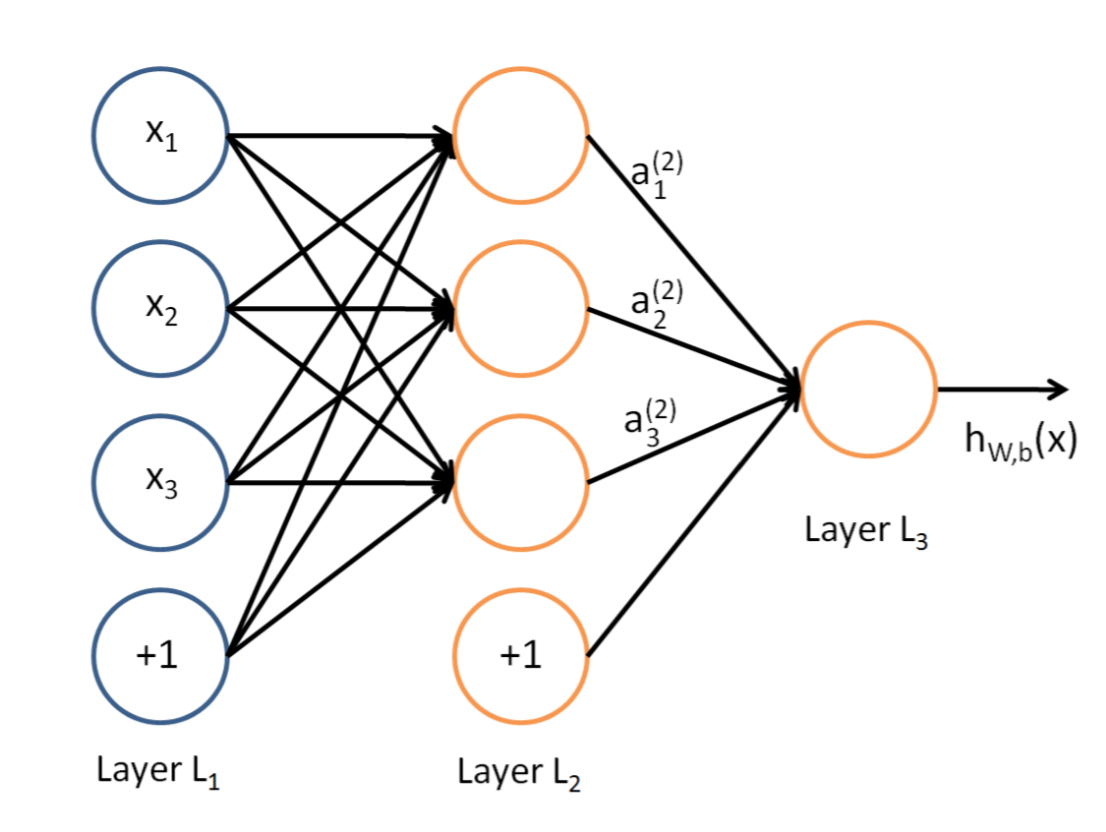
这是典型的三层神经网络的基本构成，Layer L1是输入层，Layer L2是隐含层，Layer L3是隐含层，我们现在手里有一堆数据{x1,x2,x3,...,xn},输出也是一堆数据{y1,y2,y3,...,yn},现在要他们在隐含层做某种变换，让你把数据灌进去后得到你期望的输出。如果你希望你的输出和原始输入一样，那么就是最常见的自编码模型（Auto-Encoder）。可能有人会问，为什么要输入输出都一样呢？有什么用啊？其实应用挺广的，在图像识别，文本分类等等都会用到，我会专门再写一篇Auto-Encoder的文章来说明，包括一些变种之类的。如果你的输出和原始输入不一样，那么就是很常见的人工神经网络了，相当于让原始数据通过一个映射来得到我们想要的输出数据，也就是我们今天要讲的话题。

本文直接举一个例子，带入数值演示反向传播法的过程，公式的推导等到下次写Auto-Encoder的时候再写，其实也很简单，感兴趣的同学可以自己推导下试试：）（注：本文假设你已经懂得基本的神经网络构成，如果完全不懂，可以参考Poll写的笔记：[Mechine Learning & Algorithm] 神经网络基础）

假设，你有这样一个网络层：

第一层是输入层，包含两个神经元i1，i2，和截距项b1；第二层是隐含层，包含两个神经元h1,h2和截距项b2，第三层是输出o1,o2，每条线上标的wi是层与层之间连接的权重，激活函数我们默认为sigmoid函数。

现在对他们赋上初值，如下图：

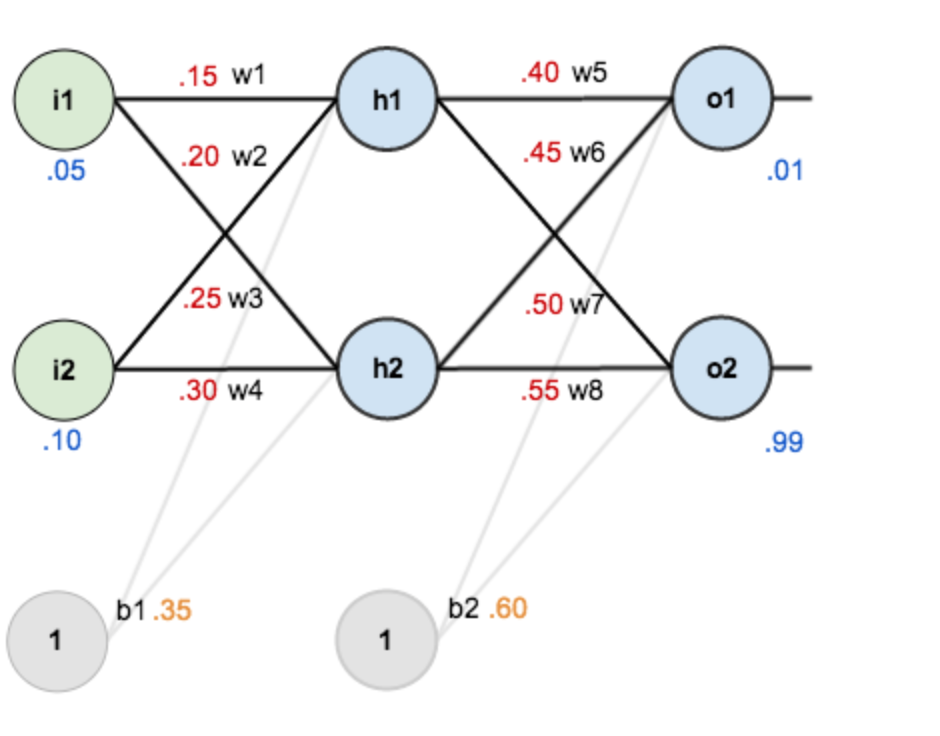
其中，输入数据 i1=0.05，i2=0.10;

　　　　　输出数据 o1=0.01,o2=0.99;

　　　　　初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;

　　　　　　　　　 w5=0.40,w6=0.45,w7=0.50,w8=0.88

　　目标：给出输入数据i1,i2(0.05和0.10)，使输出尽可能与原始输出o1,o2(0.01和0.99)接近。

Step 1 前向传播

1.输入层---->隐含层：

计算神经元h1的输入加权和：

神经元h1的输出o1:(此处用到激活函数为sigmoid函数)：

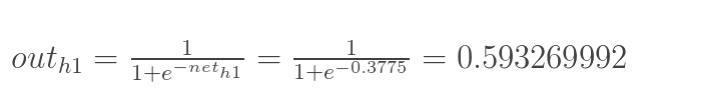
同理，可计算出神经元h2的输出o2：

2.隐含层---->输出层：

计算输出层神经元o1和o2的值：

这样前向传播的过程就结束了，我们得到输出值为[0.75136079 , 0.772928465]，与实际值[0.01 , 0.99]相差还很远，现在我们对误差进行反向传播，更新权值，重新计算输出。

Step 2 反向传播

1.计算总误差

总误差：(square error)

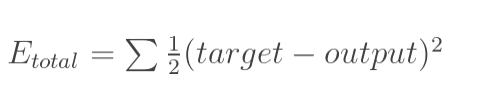
但是有两个输出，所以分别计算o1和o2的误差，总误差为两者之和：

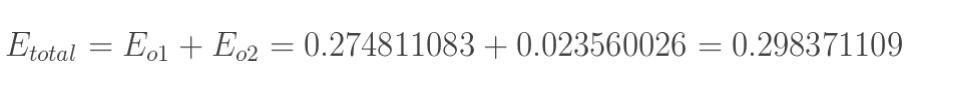
2.隐含层---->输出层的权值更新：

以权重参数w5为例，如果我们想知道w5对整体误差产生了多少影响，可以用整体误差对w5求偏导求出：（链式法则）

下面的图可以更直观的看清楚误差是怎样反向传播的：

现在我们来分别计算每个式子的值：

计算 ：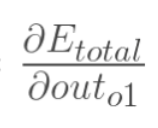

未完待续……

From: http://www.cnblogs.com/charlotte77/p/5629865.html