Neural Network Basics

在学习NLP之前还是要打好基础，第二部分就是神经网络基础。

知识点总结：

1.神经网络概要：

2. 神经网络表示：

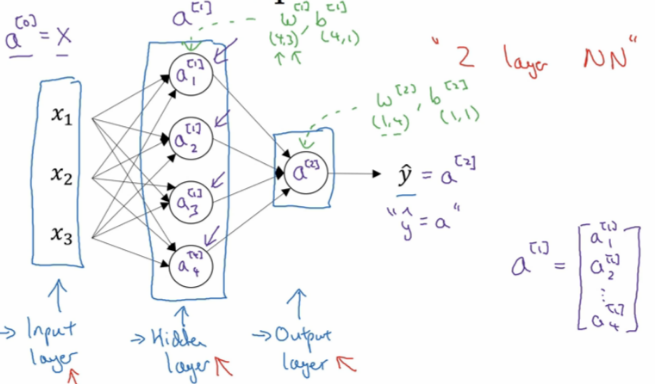
第0层为输入层（input layer）、隐藏层（hidden layer）、输出层（output layer）组成。

3. 神经网络的输出计算：

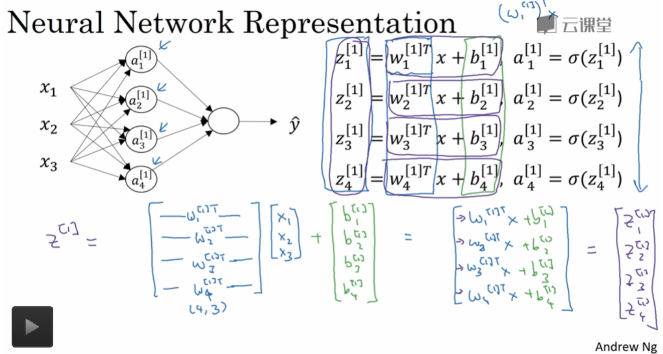
4.三种常见激活函数:

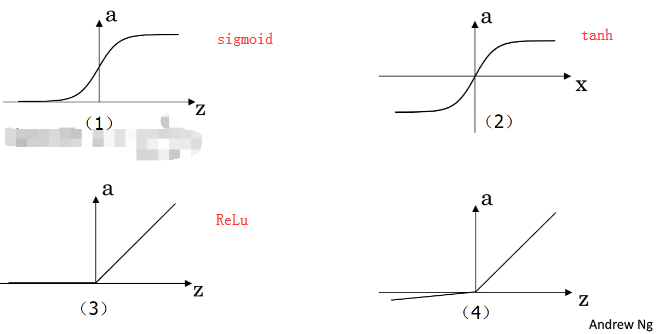
sigmoid:一般只用在二分类的输出层，因为二分类输出结果对应着0,1恰好也是sigmoid的阈值之间。

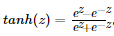。它相比sigmoid函数均值在0附近，有数据中心化的优点，但是两者的缺点是z值很大很小时候，w几乎为0，学习速率非常慢。

ReLu： f（x）= max(0, x)

• 优点：相较于sigmoid和tanh函数，ReLU对于随机梯度下降的收敛有巨大的加速作用（ Krizhevsky等的论文指出有6倍之多）。据称这是由它的线性，非饱和的公式导致的。
• 优点：sigmoid和tanh神经元含有指数运算等耗费计算资源的操作，而ReLU可以简单地通过对一个矩阵进行阈值计算得到。
• 缺点：在训练的时候，ReLU单元比较脆弱并且可能“死掉”。举例来说，当一个很大的梯度流过ReLU的神经元的时候，可能会导致梯度更新到一种特别的状态，在这种状态下神经元将无法被其他任何数据点再次激活。如果这种情况发生，那么从此所以流过这个神经元的梯度将都变成0。也就是说，这个ReLU单元在训练中将不可逆转的死亡，因为这导致了数据多样化的丢失。例如，如果学习率设置得太高，可能会发现网络中40%的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。通过合理设置学习率，这种情况的发生概率会降低。

 Assignment：

 sigmoid 实现和梯度实现：

import numpy as np

def sigmoid(x):
    f = 1 / (1 + np.exp(-x))
    return f

def sigmoid_grad(f):
    f = f * (1 - f)
    return f

def test_sigmoid_basic():
    x = np.array([[1, 2], [-1, -2]])
    f = sigmoid(x)
    g = sigmoid_grad(f)
    print (g)
def test_sigmoid():
    pass
if  __name__ == "__main__":
        test_sigmoid_basic()

#输出：
[[0.19661193 0.10499359]
 [0.19661193 0.10499359]]

　　

实现实现梯度check

import numpy as np
import random
def gradcheck_navie(f, x):
    rndstate = random . getstate ()
    random . setstate ( rndstate )
    fx , grad = f(x) # Evaluate function value at original point
    h = 1e-4
    it = np. nditer (x, flags =[' multi_index '], op_flags =[' readwrite '])
    while not it. finished :
    ix = it. multi_index
    ### YOUR CODE HERE :
    old_xix = x[ix]
    x[ix] = old_xix + h
    random . setstate ( rndstate )
    fp = f(x)[0]
    x[ix] = old_xix - h
    random . setstate ( rndstate )
    fm = f(x)[0]
    x[ix] = old_xix
    numgrad = (fp - fm)/(2* h)
    ### END YOUR CODE
    # Compare gradients
    reldiff = abs ( numgrad - grad [ix]) / max (1, abs ( numgrad ), abs ( grad [ix]))
    if reldiff > 1e-5:
    print (" Gradient check failed .")
    print (" First gradient error found at index %s" % str(ix))
    print (" Your gradient : %f \t Numerical gradient : %f" % ( grad [ix], numgrad return
    it. iternext () # Step to next dimension
    print (" Gradient check passed !")

def sanity_check():
    """
    Some basic sanity checks.
    """
    quad = lambda x: (np.sum(x ** 2), x * 2)

    print ("Running sanity checks...")
    gradcheck_naive(quad, np.array(123.456))      # scalar test
    gradcheck_naive(quad, np.random.randn(3,))    # 1-D test
    gradcheck_naive(quad, np.random.randn(4,5))   # 2-D test
    print("")  

if __name__ == "__main__":
    sanity_check()