GBDT原理
| 样本编号 | 花萼长度(cm) | 花萼宽度(cm) | 花瓣长度(cm) | 花瓣宽度 | 花的种类 |
| 1 | 5.1 | 3.5 | 1.4 | 0.2 | 山鸢尾 |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 | 山鸢尾 |
| 3 | 7.0 | 3.2 | 4.7 | 1.4 | 杂色鸢尾 |
| 4 | 6.4 | 3.2 | 4.5 | 1.5 | 杂色鸢尾 |
| 5 | 6.3 | 3.3 | 6.0 | 2.5 | 维吉尼亚鸢尾 |
| 6 | 5.8 | 2.7 | 5.1 | 1.9 | 维吉尼亚鸢尾 |
6个样本的三分类问题:
(1)三维向量标志样本的label:
[1,0,0] 表示样本属于山鸢尾,
[0,1,0] 表示样本属于杂色鸢尾,
[0,0,1] 表示属于维吉尼亚鸢尾
(2) 对每一个类训练一个CART Tree 模型: 三个树相互独立
山鸢尾类别训练一个 CART Tree 1。
杂色鸢尾训练一个 CART Tree 2 。
维吉尼亚鸢尾训练一个CART Tree 3
(3) 以样本1为例
针对CART Tree 1,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,1]
针对CART Tree 2,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,0]
针对CART Tree 3,训练样本是[5.1,3.5,1.4,0.2],label 是 1,最终输入到模型当中的为[5.1,3.5,1.4,0.2,0]
(4)CART Tree1生成:哪个特征最合适? 这个特征的什么特征值作为切分点?以CART Tree 1为例
1. 从这四个特征中找一个特征做为CART Tree1 的节点,遍历所有的可能值
1.1 第一个特征【长度】的第一个特征值【5.1cm】为例。
R1 为所有样本中花萼长度小于 5.1 cm 的样本集合,
R2 为所有样本当中花萼长度大于等于 5.1cm 的样本集合。

y1为R1样本的label均值:y1=1/1=1
y2为R2样本的label均值:y2=(1+0+0+0+0)/5=0.2
样本1属于R2的值为:(1-0.2)^2
样本2属于R1的值为:(1-1)^2
样本3属于R2的值为(0-0.2)^2
样本4属于R2的值为(0-0.2)^2
样本5属于R2的值为(0-0.2)^2
样本6属于R2的值为(0-0.2)^2
CART Tree 1在第一个特征【长度】的第一个特征值【5.1cm】的损失值为:(1-0.2)^2+ (1-1)^2 + (0-0.2)^2+(0-0.2)^2+(0-0.2)^2 +(0-0.2)^2= 0.84
1.2 第一个特征【长度】的第二个特征值【4.9cm】计算,损失值为:2.244189
1.3 遍历所有特征的特征值,查找最小的特征及特征值,特征花萼长度,特征值为5.1 cm。这个时候损失函数最小为 0.8
2. 预测函数
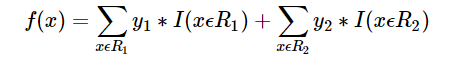
R1 = {2},R2 = {1,3,4,5,6},y1 = 1,y2 = 0.2
样本属于类别山鸢尾类别的预测值f1(x)=1+0.2∗5=2f1(x)=1+0.2∗5=2
同理我们可以得到对样本属于类别2,3的预测值f2(x)f2(x),f3(x)f3(x).样本属于类别1的概率 即为
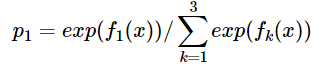
GBDT原理的更多相关文章
- GBDT原理及利用GBDT构造新的特征-Python实现
1. 背景 1.1 Gradient Boosting Gradient Boosting是一种Boosting的方法,它主要的思想是,每一次建立模型是在之前建立模型损失函数的梯度下降方向.损失函数是 ...
- 梯度提升树(GBDT)原理小结(转载)
在集成学习值Adaboost算法原理和代码小结(转载)中,我们对Boosting家族的Adaboost算法做了总结,本文就对Boosting家族中另一个重要的算法梯度提升树(Gradient Boos ...
- XGBoost,GBDT原理详解,与lightgbm比较
xgb原理: https://www.jianshu.com/p/7467e616f227 https://blog.csdn.net/a819825294/article/details/51206 ...
- 手撸GBDT原理(未完成)
一直对GBDT里面的具体计算逻辑不太清楚,在网上发现了一篇好博客. 先上总结的关系图 GBDT对类别变量是怎么处理的? 这些东西都是在网上发现的,讲的挺好的. GBDT原理与Sklearn源码分析-回 ...
- 机器学习入门:极度舒适的GBDT原理拆解
机器学习入门:极度舒适的GBDT拆解 本文旨用小例子+可视化的方式拆解GBDT原理中的每个步骤,使大家可以彻底理解GBDT Boosting→Gradient Boosting Boosting是集成 ...
- 梯度提升树(GBDT)原理小结
在集成学习之Adaboost算法原理小结中,我们对Boosting家族的Adaboost算法做了总结,本文就对Boosting家族中另一个重要的算法梯度提升树(Gradient Boosting De ...
- GBDT原理实例演示 1
考虑一个简单的例子来演示GBDT算法原理 下面是一个二分类问题,1表示可以考虑的相亲对象,0表示不考虑的相亲对象 特征维度有3个维度,分别对象 身高,金钱,颜值 cat dating.txt ...
- GBDT原理学习
首先推荐 刘建平 的博客学习算法原理推导,这位老师的讲解都很详细,不过GBDT的原理讲解我没看明白, 而是1.先看的https://blog.csdn.net/zpalyq110/article/de ...
- GBDT原理实例演示 2
一开始我们设定F(x)也就是每个样本的预测值是0(也可以做一定的随机化) Scores = { 0, 0, 0, 0, 0, 0, 0, 0} 那么我们先计算当前情况下的梯度值 ...
- GBDT原理详解
从提升树出发,——>回归提升树.二元分类.多元分类三个GBDT常见算法. 提升树 梯度提升树 回归提升树 二元分类 多元分类 面经 提升树 在说GBDT之前,先说说提升树(boosting tr ...
随机推荐
- notepad++查看二进制文件
1.进入以下网址去下载 https://sourceforge.net/projects/npp-plugins/files/Hex%20Editor/Hex%20Editor%20Plugin%20 ...
- springboot-day02-整合mybatis与简单使用
前言:该文章是紧接上一篇文章springboot-day01-引入如何读取配置文件以及helloWorld 1.springboot整合mybatis 1.添加jar包依赖 <?xml vers ...
- SpringMVC Controller 单例 多例
对于SpringMVC 的Controller单例还是多例.下面举例说明:第一次:类是多例,类里包含一个普通属性,一个静态属性 结果:普通属性:0.............静态属性:0 普通属性:0. ...
- scrapy 使用代理ip
1.在settings文件中添加ip池 IPPOOL=['xxx.xx.xx.xx','xxx.xx.xxx.xx'] 2.在middleware文件中添加自己的代理ip类(首先需要导入ipPOOL, ...
- oracle 查询列表中选取其中一行
select k.SAL from (select SAL,rownum rn from (select SAL from SCOTT.EMP where MGR = 7698 order by SA ...
- linux下访问window的共享文件,在命令行实现方法
1.挂载共享目录 mount -t cifs //192.168.0.1/aa /tmp/export -o username=text,password=test //192.168.0.1/aa ...
- linux下主从同步和redis的用法
前言 mariadb其实就是mysql mysql已经被oracle收购,它即将闭源,马上要开始收费了因此还想免费试用开源的数据库mysql,就在centos7上,将mysql分支为mariadb 操 ...
- 大数据hadoop的伪分布式搭建
1.配置环境变量JDK配置 1.JDK安装 个人喜欢在 vi ~/.bash profile 下配置 export JAVA_HOME=/home/hadoop/app/jdk1.8.0_91ex ...
- 如何利用FPGA进行时序分析设计
FPGA(Field-Programmable Gate Array),即现场可编程门阵列,它是作为专用集成电路(ASIC)领域中的一种半定制电路而出现的,既解决了定制电路的不足,又克服了原有可编程器 ...
- unity缓动插件DOTween Pro v0.9.680
DoTween Pro是一款unity插件,是unity中最好用的tween插件,比起Dotween的免费版要多很多功能,实现脚本和视觉脚本的新功能,支持包括移动,淡出,颜色,旋转,缩放,打孔,摇动, ...
