GBDT算法

GBDT通过多轮迭代,每轮迭代产生一个弱分类器，其中弱分类器通常选择为CART树，每个分类器在上一轮分类器的残差基础上进行训练。

对于GBDT算法，其中重要的知识点为：

1、GBDT是梯度下降法从参数空间上升到函数空间的算法

2、其属于集成算法Boosting

3、损失函数的构造

一、GBDT损失函数

　　下面对于其损失函数做简单的讲解：

　　GBDT的模型如下，其中T表示每棵树，总共集成了M颗。

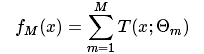
　　其损失函数表示：

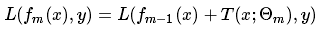
　　对于其中的L函数该如何选择，也就是关系到GBDT的损失函数构造问题了。一般来说，对于分类问题，选择对数损失；对于回归问题，选择最小二乘损失。

二、梯度下降

　　GBDT是梯度下降法从参数空间上升到函数空间的算法，也就是说，他的梯度求导，是关于树函数的。这也很好理解，通常我们求决策树的损失函数，是为了评价树的质量，而不是根据损失函数求参数，因为树的构造不需要损失函数，直接通过信息增益、信息增益率、基尼系数等构造的。但是N颗树该如何构造，也就是说每棵树需要达到什么样的效果对于GBDT的损失函数最小，这才是其梯度下降需要关注的。