luoguP3768 简单的数学题

题目链接

luoguP3768 简单的数学题

题解

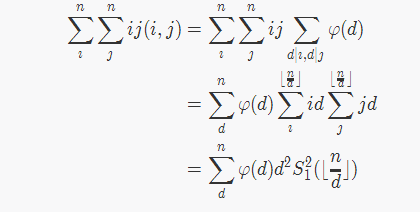
上面那个式子的最后一步，需要定理

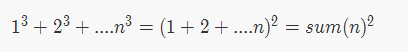
用数学归纳法证明

\(S1=1^3=1^2\)

\(S2=1^3+2^3=9=3^2=(1+2)^2\)

\(S3=1^3+2^3+3^3=36=6^2=(1+2+3)^2\)

\(S4=1^3+2^3+3^3+4^3=100=10^2=(1+2+3+4)^2\)

\(S5=1^3+2^3+3^3+4^3+5^3=15^2=(1+2+3+4+5)^2\)

假设当\(n=k\)时，有\(Sk=1^3+2^3+...+k^3=(1+2+...+k)^2\)

则当\(n=(k+1)\)时，

\(S(k+1)=Sk+ak=(1+2+...+k)^2+(k+1)^3\)

\(=[k(k+1)/2]^2+(k+1)^3\)

\(=(k+1)^2[k^2/4+k+1]\)

\(=(k+1)^2[(k^2+4k+4)/4]\)

\(=(k+1)^2(k+2)^2/4\)

\(=[(k+1)(k+2)/2]^2\)

\(=(1+2+...+k+1)^2\)

对于前面那个杜教筛

代码

#include<map>
#include<cstdio>
#include<algorithm> 
inline int read() {
	int x = 0,f = 1;
	char c = getchar();
	while(c < '0' || c > '9') { if(c == '-')f = -1; c = getchar(); }
	while(c <= '9' && c >= '0') x = x * 10 + c - '0',c = getchar();
	return x * f;
}
#define LL long long
const int maxn = 10000000;
LL Max = maxn; 
std:: map<LL,LL>M;
LL Inv6,Inv2,Phi[maxn + 7], phi[maxn + 7],mod;
bool isprime[maxn + 7];
int prime[maxn],cnt = 0; 
LL fstpow(LL a,LL b) {
    LL ret = 1;
    for(;b;b >>= 1,a = a * a % mod)
        if(b & 1) ret = ret * a % mod;
    return ret;
}  
void getphi() {
	phi[1] = 1;
	for(int i = 2;i <= Max;++ i) {
		if(!isprime[i]) prime[++ cnt] = i,phi[i] = (i - 1) % mod;
		for(int j = 1;j <= cnt && i * prime[j] <= Max;++ j) {
			isprime[i * prime[j]] = 1;
			if(i % prime[j]) phi[i * prime[j]] = 1ll * phi[i] * phi[prime[j]] % mod;
			else {
				phi[i * prime[j]] = 1ll * phi[i] * prime[j] % mod;
				break;
			}
		}
	}
	for(int i = 1;i <= Max;++ i) Phi[i] = 1ll * phi[i] * i % mod * i % mod;
	for(int i = 1;i <= Max;++ i) Phi[i] += Phi[i - 1] , Phi[i] %= mod;
}
//---------------------------------------------
LL S1(LL r) { r %= mod;return r * (r + 1) % mod * (r + r + 1) % mod * Inv6 % mod; }
LL S2(LL r) { r %= mod;return r * (r + 1) % mod * Inv2 % mod; }
LL S(LL n) {
	if(n <= maxn) return Phi[n];
	if(M[n])      return M[n];
	LL he = S2(n) * S2(n) % mod , t;
	for(LL i = 2,l;i <= n;i = l + 1) {
		l = n / (n / i);
		t = ((S1(l) - S1(i - 1)) % mod + mod) % mod;
		he -= t * S(n / i) % mod,he %= mod;
	}
	return M[n] = (he + mod) % mod;
}
LL solve(LL n) {
	LL res = 0;
	for(LL i = 1,l,t ;i <= n;i = l + 1) {
	    l = n / (n / i),t = S2(n/i);
		res += ((S(l) - S(i - 1) + mod) % mod * (t * t % mod)) % mod;
		res %= mod;
	}
	return (res + mod) % mod;
} 
int main() {
	LL n;
	scanf("%lld%lld",&mod,&n);
	Max = std::min(Max,n);
	Inv2 = fstpow(2,mod - 2),Inv6 = fstpow(6,mod-2);
	getphi();
	printf("%lld\n",solve(n));
	return 0;
}