【洛谷P3410】拍照题解（最大权闭合子图总结）

题目描述

小B有n个下属，现小B要带着一些下属让别人拍照。

有m个人，每个人都愿意付给小B一定钱让n个人中的一些人进行合影。如果这一些人没带齐那么就不能拍照，小B也不会得到钱。

注意：带下属不是白带的！！！对于每个下属，如果他带了那么小B需要给他一些钱，保证当他拍照时配合。

请问，小B的净收益最多是多少。

输入输出格式

输入格式：

第1行有2个正整数m和n（0<m,n<=100）。接下来的m行，每行是一个要求拍照的人的有关数据。第一个数是他同意支付该合影的费用；接着是该合影需要的若干下属的编号，以一个0作为行的结束标记。最后一行的n个数是带每个下属的费用。

输出格式：

一个数，表示最大收益。小B可以一个人也不带。

题解

　　我们把题目用图的形式表示出来：我们把所有的要求看作是点，每个要求的收益看作是这个点的点权，同理每个人也看作是点，每个人的花费的相反数看作是这个点的点权，然后在每个要求与人之间连接有向边。

　　就可发现，我们所求的其实就是这个图的最大权闭合子图。

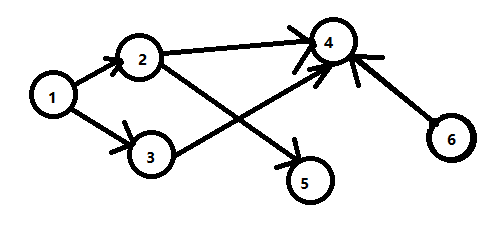
　　首先，我们先来解释一下什么叫做闭合图，所谓最大权闭合图指的是对于一个点集，从这个点集中的点出发的所有出边所指向的点也在这个点集中，则这个点集所组成的图就是一个闭合图。举个例子来说：如下图所示，点集{1，2，3，4，5}和点集{1，2，3，4，5，6}所组成的图都是闭合图，而点集{1，2，3，5，6}就不是一个闭合图（6有一条出边指向了4，但是4没在点集中）。而所谓的最大权，就是指的这样的图中点权和最大的。

　　求解最大权的闭合子图我们通常是利用网络流进行求解，我们构造一个超级源点（s），把所有的点权为正的点都与之连边，边的容量为这些点的点权；再构造一个超级汇点（t），把所有的点权为负的点都与之连边，边的容量为点权的相反数，另外，这些点之间原有的边保持不变，边的容量为正无穷。即如下图（黑色为点的编号，红色为权值）：

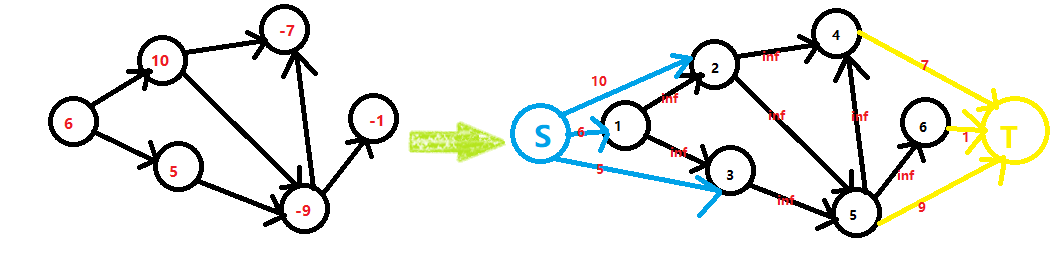
　　我们来研究以下两个图之间有什么关系：

• 在第二个图中，关于s-t的最小割是简单割（割边都与S或T相连），显然他不会去割无穷大的边（黑色的边）。
• 第二个图的关于s-t的每一个简单割产生的两个子图，我们把含有S的称作S图，含有T的称作T图。则S图是闭合子图。

证明：
简单割中不包含无穷大的边（黑色的边），即不包含联通两个图的边（连接在T点上的边除外）。

所以S图中的边所指向的点一定在S图中，即为闭合图。

• 最小割产生的S图和T图，S图为最大权闭合子图。

证明：

　　因为割集中所有的边，不是连接在s上，就是连接在t上；

　　我们记割集中，所有连接在s上的边的权值和为x1，所有连接在t上的边的权值和为x2，而割集中所有边权值和为X=x1+x2；

　　又，记图S中所有点的权值和为W，记其中正权值之和为w1，负权值之和为 - w2，故W = w1 - w2；

　　而 W + X = w1 - w2 + x1 + x2，由于x2 = w2

　　　　（因为图S中所有负权值的点，必然连接到t点，而图S必然要与t分割开；故割集中，“连接在t点上的边权值和”就是“图S中所有负权值点的权值之和，取负”）

　　因而W + X = w1 + x1；

　　而显然的，w1 + x1是整个图中所有正权值之和，记为SUM；

　　故W = SUM - X，即 “图S中所有点的权值和” = “整个图中所有正权值之和”  - “割集中所有边权值和”；

　　然后，因为SUM为定值，只要我们取最小割，则“图S中所有点的权值和”就是最大的，即此时图S为图S为最大权闭合子图。

　　所以最大权闭合子图的点权之和等于收益点权之和减去最小割。

代码

#include<bits/stdc++.h>
using namespace std;

int w[], c[];
vector <int> G[];
int n, m, x;
const int inf = 0x7fffffff;

class Graph{
    private :
        int cnt;
        int Head[], Next[], W[], To[];
        int Deep[], cur[];
    public :
        int s, t, n;
        void init()
            {
                cnt = -;
                memset(Head, -, sizeof(Head));
                memset(Next, -, sizeof(Next));
            }
        void _Add(int u, int v, int c)
            {
                Next[++ cnt] = Head[u];
                Head[u] = cnt;
                W[cnt] = c;
                To[cnt] = v;
            }
        void Add_edge(int x, int y, int w)
            {
                _Add(x, y, w);
                _Add(y, x, );
            }
        int Dfs(int u, int flow)
            {
                if(u == t)    return flow;
                for(int & i = cur[u]; i != -; i = Next[i])
                    {
                        if(Deep[To[i]] == Deep[u] +  && W[i] != )
                            {
                                int di = Dfs(To[i], min(flow, W[i]));
                                if(di > )
                                    {
                                        W[i] -= di;
                                        W[i ^ ] += di;
                                        return di;
                                    }
                            }
                    }
                return ;
            }
        int Bfs()
            {
                queue <int> q;
                for(; !q.empty();)    q.pop();
                memset(Deep, , sizeof(Deep));
                Deep[s] = ; q.push(s);
                for(; !q.empty();)
                    {
                        int u = q.front(), v; q.pop();
                        for(int i = Head[u]; i != -; i = Next[i])
                            if(!Deep[v = To[i]] && W[i])
                                {
                                    Deep[v] = Deep[u] + ;
                                    q.push(v);
                                }
                     }
                return Deep[t] >  ?  : ;
            }
        int Dinic()
            {
                int ans;
                for(;Bfs();)
                    {
                        for(int i = ; i <= n; ++ i)    cur[i] = Head[i];
                        int d;
                        for(;d = Dfs(s, inf);)    ans += d;
                    }
                return ans;
            }
};

Graph Map;
int Num = ;
int n1[], n2[];

void Make_picture()
    {
        Map.s = ++ Num;
        for(int i = ; i <= n; ++ i)
            {
                n1[i] = ++ Num;
                Map.Add_edge(Map.s, Num, w[i]);
            }
        for(int i = ; i <= m; ++ i) n2[i] = ++ Num;
        Map.n = Map.t = ++ Num;
        for(int i = ; i <= m; ++ i) Map.Add_edge(n2[i], Map.t, c[i]);
        for(int i = ; i <= n; ++ i)
            for(int j = ; j < G[i].size(); ++ j)
                Map.Add_edge(n1[i], n2[G[i][j]], inf);
        return ;
    }
int sum = ;
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = ; i <= n; ++ i)
        {
            scanf("%d", &w[i]);
            sum += w[i];
            for(;;)
                {
                    scanf("%d", &x);
                    if(!x) break;
                    G[i].push_back(x);
                }
        }
    for(int i = ; i <= m; ++ i)    scanf("%d", &c[i]);
    Map.init();
    Make_picture();
    printf("%d\n", sum - Map.Dinic());
    return ;
}

参考资料

[1]Dilthey's Blog:最大权闭合子图-[求最大点权的闭合子图]

[2]洛谷【P3410】拍照