Codeforces Global Round 16题解

E. Buds Re-hanging

对于这个题该开始还是没想法的，但这显然是个思维题，还是要多多动手推样例，实践一下。

简化题意：给定一个有根树，规定某个点为树干，当且仅当这个点不是根，且这个点至少有一个儿子，这个点的所有儿子都是叶子节点。每次可以将一个树干及其子树分离出来，然后将这个点与树上其他点相连。问：进行若干次操作之后，整个树的最少的叶子结点的个数？

首先我思考的是：我们这个树干从原来的父亲节点摘下来后要放到哪里，可以发现如果练到一个非叶子节点上的话，总的叶子数量是不会减少的，甚至有可能增多(因为原本树干的父亲可能成为新的叶子)。所以最优的情况一定是将这个树干连到一个叶子节点上。可以发现对于任意一个树的结构我们都可以从叶子节点往上，依次将他们拆离，也就是每次都将当前所有的树干摘离，那么最后只有两种结果，根节点不能被拆离，只剩下根节点一个点，根节点也能被摘离，整棵树都能被拆离。那么对于当前一个点x而言，我们要如何操作，才能使得整个的叶子节点最少。对于x的所有儿子y，我们期望的最优结果就是所有儿子都能够摘离除去，放到其中一个儿子身上，类似一个链的形状。这样的话，叶子节点最少。考虑这样我们需要儿子的那些信息，如何统计答案？首先需要儿子能不能被完全摘离，还有儿子内部经过调整之后的最少的叶子节点。起初令\(ans[x]=\sum ans[y]\)，之后，若有一个儿子能够完全被摘离，那\(ans[x]--\)，因为我们可以将y这个儿子及其子树全部摘离，放到另一个子树上，减少一个叶子结点。但有一种情况比较特殊，就是当全部的儿子都能被摘离时，我们要将\(ans[x]++\)，因为我们至少留一个儿子放上面。那么考虑x是否能被摘离，若x的全部儿子都能被摘离，则x不能被摘离，否则x就能被摘离。直接树形DP即可。

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int n,f[N];
vector<int>son[N];
inline bool dfs(int x,int fa)//bool表示能不能被摘离.
{
	int children=0,cnt=0;//cnt表示能被摘离的儿子的个数。
	for(auto y:son[x])
	{
		if(y==fa) continue;
		children++;
		if(dfs(y,x)) cnt++;
		f[x]+=f[y];
	}
	f[x]-=cnt;
	if(cnt==children) f[x]++;
	if(children==0) {f[x]=1;return 0;}
	return (cnt==children)?0:1;
}
int main()
{
//	freopen("1.in","r",stdin);
	int T;cin>>T;
	while(T--)
	{
		cin>>n;
		for(int i=1;i<=n;++i) son[i].clear();
		for(int i=1;i<n;++i)
		{
			int x,y;cin>>x>>y;
			son[x].push_back(y);
			son[y].push_back(x);
		}
		memset(f,0,sizeof(f));
		dfs(1,0);
		cout<<f[1]<<endl;
	}
	return 0;
}

F. Points Movement

简化题意：给定你一些点和区间，点可以左右移动，当一个点处于某个线段中时成这个区间被访问过，问最少移动的次数使得所有的区间被访问过?

首先可以发现一些小的结论，若某个区间完全包含另一个区间的话，则那个大的区间就不必考虑了，因为若访问过小的区间，则大的区间也一定被访问了。其次，对于初始位置而言，若某个点在某个区间内的话，则这个区间也不用被考虑。这样的话，我们将不必考虑的区间都剔除，考虑剩下的区间和点构成什么了？我们将区间按左端点排序，可以发现右端点一定也是有序的，若出现有序，则一定会出现大包小的情况，在第一步就被我们剔除掉了。剩下的点和区间一定是相间分布的，即点，区间，点，区间...这样分布的，其次我们考虑某个区间被访问时一定只是其端点被访问，且访问的点一定是向左，向右离他最近的点，也就是说点的移动不会跨过另一个点，否则我们移动另一个点一定更优。

考虑以下这个区间我们有多少种情况：



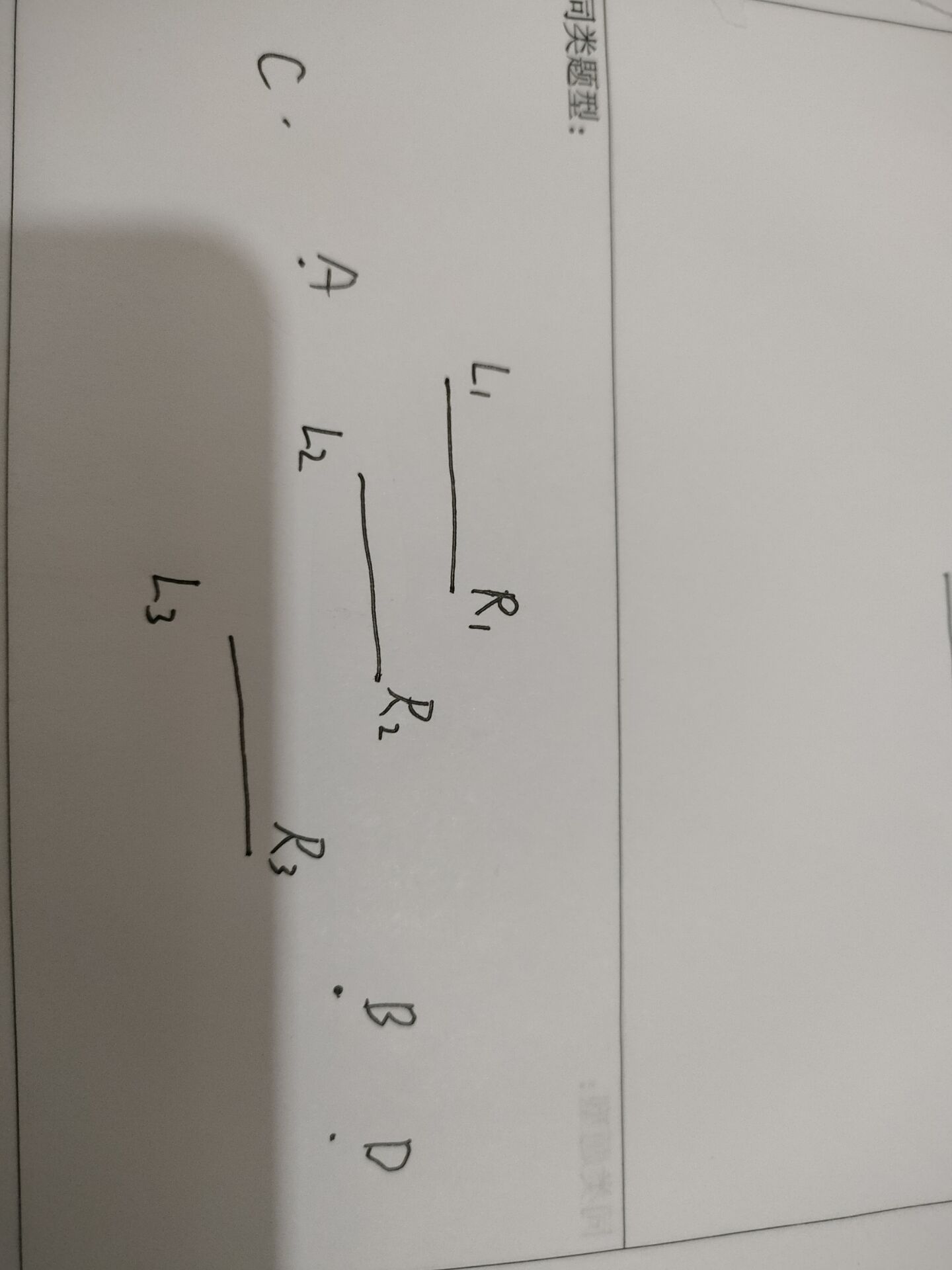
首先这三个区间我们一定是用A和B移动去访问他们，那这里就有以下方案：

1.A去\(L_3\)

2.A去\(L_2\),B去\(R_3\)

3.A去\(L_1\),B去\(R_2\)

4.B去\(R_1\)

发现这里的方案数为O(K)k是区间的数量。但考虑到如果某两个区间的中间夹的点数只有一个。那么这个点可能先往左边跑，之后再往右边跑，这个怎么解决，所以我们需要知道点的位置。由于每个点左右跑的话一定会回到原位置，所以我们可以分开统计答案，每个点可以到某个区间端点不动了，也可以到区间端点再返回原位置，所以我们记录f[i][0/1]表示第i个点之前所有的区间都访问过，且这个点不返回位，返回原位，的最少的移动步数。注意这里点左右跑的话可能有两个选择，可以先向左边跑，再向右边跑，也可以先向右边跑，再向做边跑。注意转移状态的时候别漏就行。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+10;
int n,m;
ll f[N][2],a[N],L[N],R[N];
struct segment{int l,r;};
vector<segment>v;
inline bool cmp(segment x,segment y)
{
	return (x.l!=y.l)?(x.l<y.l):(x.r>y.r);
}
int main()
{
    //freopen("1.in","r",stdin);
	int T;cin>>T;
	while(T--)
	{
		scanf("%d%d",&n,&m);
		for(int i=1;i<=n;++i) scanf("%lld",&a[i]);
		sort(a+1,a+n+1);v.clear();
		for(int i=1;i<=m;++i)
		{
			int l,r;scanf("%d%d",&l,&r);
			int id=lower_bound(a+1,a+n+1,l)-a;
			if(id==n+1||a[id]>r)
			{
				v.push_back((segment){l,r});
			}
		}
		sort(v.begin(),v.end(),cmp);
		for(int i=0;i<v.size();++i)
		{
			if(i!=0&&v[i].r<=v[i-1].r)
			{
				v.erase(v.begin()+i-1);
				i-=2;
			}
		}
		for(int i=1;i<=n+1;++i) f[i][0]=f[i][1]=1e18;
		f[0][0]=f[0][1]=0;
		a[0]=-1e18;a[n+1]=1e18;
		int now=0;//now表示当前处理到的区间。
		for(int i=1;i<=n+1;++i)
		{
			int cnl=0,cnr=0;//L表示左边点到达的终点，R表示右边点到达的终点。
			L[++cnl]=a[i-1];
			while(now<v.size()&&v[now].r<a[i])
			{
				L[++cnl]=v[now].l;
				R[++cnr]=v[now].r;
				++now;
			}
			R[++cnr]=a[i];
			for(int j=1;j<=cnl;++j)
			{
				f[i][0]=min(f[i][0],f[i-1][1]+L[j]-a[i-1]+a[i]-R[j]);
				f[i][1]=min(f[i][1],f[i-1][1]+L[j]-a[i-1]+(a[i]-R[j])*2);
				f[i][0]=min(f[i][0],f[i-1][0]+(L[j]-a[i-1])*2+a[i]-R[j]);
				f[i][1]=min(f[i][1],f[i-1][0]+(L[j]-a[i-1])*2+(a[i]-R[j])*2);
			}
		}
		printf("%lld\n",min(f[n+1][1],f[n+1][0]));
	}
	return 0;
}