hisql 高级功能数据检测将错误数据拦截在系统外 一

hisql github源码下载

git clone https://github.com/tansar/HiSql.git

在设计第二范式数据库时经常会把可能重复的数据单独做一种表关联，但是在写入表时为了数据的严谨需要校验一下值在另外一张表中存不存在

如 用一张用户表（HTest01) 该表表结构如下

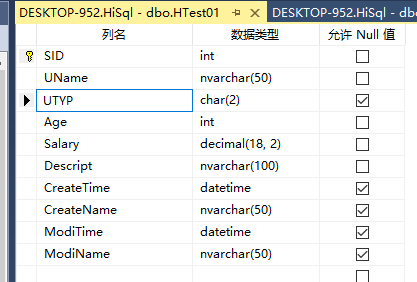
其中字段UTYP 的值在另外一张表H_UType中做了维护表结构如下

为了演示使用我们向H_UType 中写入三条数据如下所示

//在表中添加用户类型 Modi方法的意思是 如果存在则更新没有则插入
            sqlClient.Modi("H_UType", new List<object> {
                new { UTYP = "U1", UTypeName = "普通用户" },
                new { UTYP = "U2", UTypeName = "中级用户" },
                new { UTYP = "U3", UTypeName = "高级用户" }
            }).ExecCommand();

正常我们向表HTest01 写入数据时字段UTYP 的值必须要存在于表H_UType中 不然这条数据就是一条不符合逻辑的数据，也可以认为这是条脏数据，在写代码时如果没有做一些校验就有可有把这种数据成功保存到数据库中

HiSql 作者在日常开发过种也经常碰到这种问题，特别是在多业务场景多人团队开发时尤为明显有些开发考虑的全一点就做了校验有些就忽略了，带来系统的Bug的隐患 ，那有没有一种方式可以杜绝这种基本的逻辑错误呢？

Hisql 提供了这个功能，使用过HiSql的用户肯定知道 在初化始了HiSql后会产生四张标准表如下所示

Hi_TabModel

Hi_FieldModel

Hi_Domain

Hi_DataElement

但这里不重点把每张表的作用一一介绍，我们需要实现本篇讲的数据检测只需要修改一下配置表Hi_FieldModel 代码如下

sqlClient.Update("Hi_FieldModel", new { TabName = "HTest01", FieldName = "UTYP", IsRefTab=true,RefTab= "H_UType",RefField="UTYP", RefFields = "UTYP,UTypeName",RefFieldDesc= "类型编码,类型名称",RefWhere="UTYP<>''" }).ExecCommand();

执行以上更新代码就是将表HTest01 的字段UTYP 配置了向该表插入数据时 字段UTYP 的值必须要是在表H_UType 中的字段UTYP 中，那么在向表HTest01 写入数据时HiSql底层将会自动进行校验

可能大家会担心是不是每条数据都会查表校验会不会有性能问题，其实不用担心 HiSql对这些已经做了特殊处理基本上不用担心如果大家感兴趣可以查看一下HiSql的源码

那么我们就试一试向表HTest01插入数据测试一下看

sqlClient.Insert("HTest01", new { SID = "0", UTYP = "U4", UName = "hisql", Age = 36, Salary = 11, Descript = "hisql" }).ExecCommand();

执行以上代码会出现什么情况呢？ 是的会抛出异常如下所示

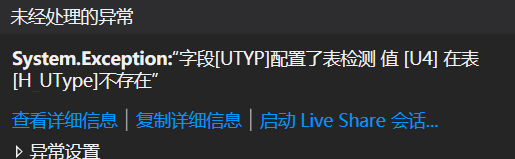
这是HiSql 底层检测完后抛出的异常，以上代码插入的字段UTYP 值U4 不在刚才配置的表H_UType 中，所以这是一种不符合正常业务逻辑的非法数据

修改一下代码

sqlClient.Insert("HTest01", new { SID = "0", UTYP = "U3", UName = "hisql", Age = 36, Salary = 11, Descript = "hisql" }).ExecCommand();

这样就可以正常执行了可以通过HiSql 校验