1336 - Sigma Function

1336 - Sigma Function

PDF (English)

Statistics

Forum

Time Limit: 2 second(s)

Memory Limit: 32 MB

Sigma function is an interesting function in Number Theory. It is denoted by the Greek letter Sigma (σ). This function actually denotes the sum of all divisors of a number. For example σ(24) = 1+2+3+4+6+8+12+24=60. Sigma of small numbers is easy to find but for large numbers it is very difficult to find in a straight forward way. But mathematicians have discovered a formula to find sigma. If the prime power decomposition of an integer is

Then we can write,

For some n the value of σ(n) is odd and for others it is even. Given a value n, you will have to find how many integers from 1 to n have even value of σ.

Input

Input starts with an integer T (≤ 100), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 10¹²).

Output

For each case, print the case number and the result.

Sample Input	Output for Sample Input
4 3 10 100 1000	Case 1: 1 Case 2: 5 Case 3: 83 Case 4: 947

---

Problem Setter: Shahriar Manzoor

Special Thanks: Jane Alam Jan (Solution, Dataset)

思路：他让求的是偶数的个数，所以我们可以求奇数的个数因为从公式中看，如过要为偶数的话其中有一项为偶数就可以了，如果要为奇数的话所有的都要是奇数，目前我们还不知道

那个方向简单，我们可以两方向都考虑下，最后会发现求奇数方案可行。素数中除了2以外全为奇数，如果数中含有2因子，那么（p1）^e1+1/(p1-1)肯定为奇数，这个很好证明，如果p1

为其它素数，如果（（p1）^e1+1-1）/(p1-1)要为奇数那么e1必定为偶数，我们可以用二项展开证明

因为p1为奇数，设p1=2*k+1；将p1代入，

所以要为奇数的话e1必定要是偶数。所以从1，循环到sqrt(n)，因为要素数的幂是偶数次那么（除了2的幂可以为奇数可以为偶数），所以判定下（i*i）<=n和2*i*i<=n有多少就行了。

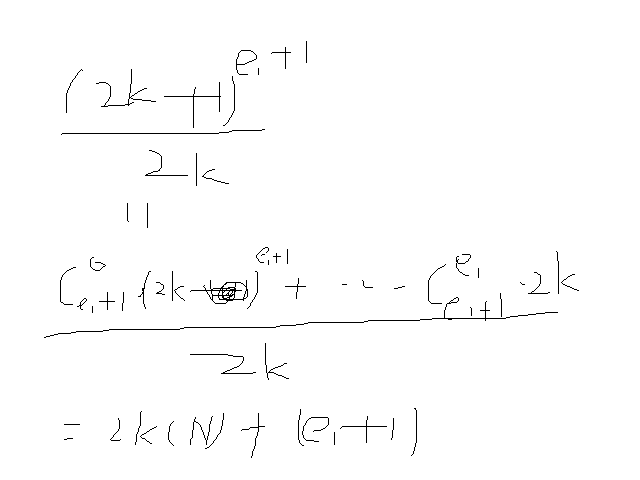
 1 #include<stdio.h>
 2 #include<algorithm>
 3 #include<iostream>
 4 #include<string.h>
 5 #include<math.h>
 6 using namespace std;
 7 typedef long long LL;
 8 int main(void)
 9 {
10         int i,j,k,p,q;
11         LL ans;
12         scanf("%d",&k);
13         int s;
14         for(s=1; s<=k; s++)
15         {
16                 scanf("%lld",&ans);
17                 LL cnt=0;
18                 for(j=1; j<=sqrt(1.0*ans); j++)
19                 {
20                         LL bns=(LL)j;
21                         if(bns*bns<=ans)
22                         {
23                                 cnt++;
24                         }
25                         if(2*bns*bns<=ans)
26                         {
27                                 cnt++;
28                         }
29                 }
30                 printf("Case %d: ",s);
31                 printf("%lld\n",ans-cnt);
32         }
33         return 0;
34 }

复杂度O（sqrt(n)）;