洛谷 P5280 - [ZJOI2019]线段树（线段树+dp，神仙题）

题面传送门

神仙 ZJOI，不会做啊不会做/kk

Sooke：“这八成是考场上最可做的题”，由此可见 ZJOI 之毒瘤。

首先有一个非常显然的转化，就是题目中的“将线段树分裂成两棵线段树”，我们事实上大可不必真的把线段树一分为二，可以看作对于操作集合 \(S\) 的所有子集 \(S'\subseteq S\) 计算出执行 \(S'\) 中的操作后线段树上有多少个节点 tag 为 \(1\)。

其次建好线段树，我们考虑一次操作 \([l,r]\) 会对哪些节点产生影响。不妨举个例子，比方说 \(n=6,l=3,r=4\)，那么建出线段树来就如下图所示：

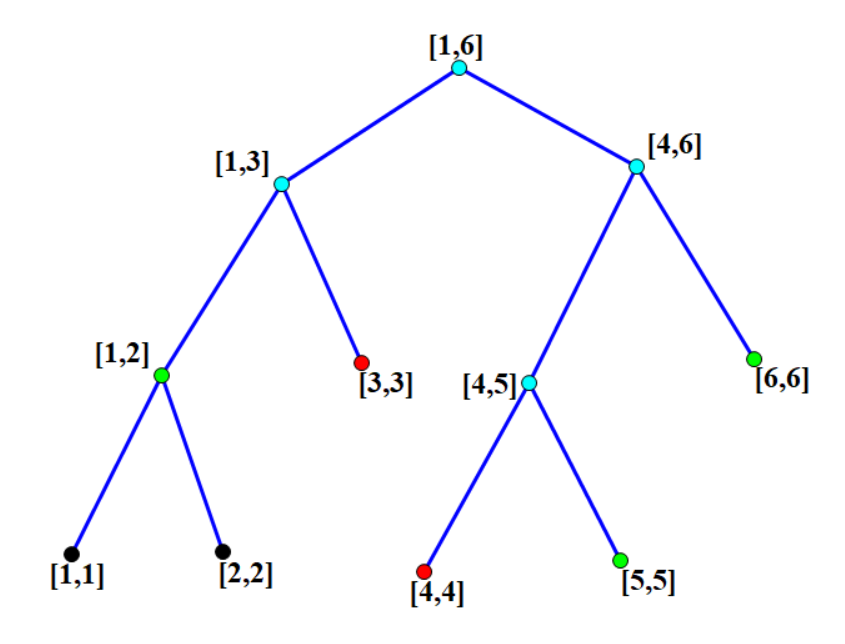
不难发现：

• 对于图中标浅蓝色的节点，在递归过程中会被遍历到，它们的标记一定会被推向它们的左右儿子，故此次修改结束后它们的 \(tag\) 一定为 \(0\)。我们不妨称之为Ⅰ类点。
• 对于图中标红色的节点，它们所表示的区间完全包含于 \([l,r]\) 中，也就是说，当我们递归到这样的节点时我们会在它上面打上 \(1\) 的 \(tag\) 并返回。故此次修改结束后它们的 \(tag\) 一定为 \(1\)。我们不妨称之为Ⅱ类点。

可我们一次修改只会对这两类点的 \(tag\) 值产生影响吗？

注意到上图中还有一类点被我们用绿色标了出来，对于这样的节点，虽然我们不会直接访问它们，但它们的祖先全部都是Ⅰ类点，故我们在标记下传的过程中，如果存在它的某个 \(tag\) 为 \(1\) 祖先，那么该祖先的 \(tag\) 一定会传到该节点。我们如法炮制地称这样的节点为Ⅲ类点。

我们把每次修改影响的节点弄清楚了，可怎么计算答案呢？

考虑 \(dp\)，可以非常自然地想到 \(dp_i\) 表示当前状态下有多少个操作子集使节点 \(i\) 的 \(tag\) 为 \(1\)。不过直接 \(dp\) 似乎是不太可行的（也不是不行，只是细节多一些，因为要下传一些标记），这里用到了一个我想不到的套路——方案数转期望，也就是说我们将每个 \(dp_i\) 都除以 \(2^{|S|}\)，其中 \(S\) 为当前操作集合。最终得到的 \(dp_i\) 显然是随便选一个集合，使得 \(tag_i=1\) 的概率，那么最终的答案显然为 \(\sum dp_i\times 2^{|S|}\)。

接下来考虑 \(dp_i\) 的转移：

• 对于Ⅰ类点，有 \(1/2\) 的概率不执行该操作，\(tag\) 保持不变，有 \(1/2\) 的概率执行该操作，\(tag\) 保持变为 \(0\)，故 \(dp_i=\dfrac{dp_i}{2}\)

• 对于Ⅱ类点，有 \(1/2\) 的概率不执行该操作，\(tag\) 保持不变，有 \(1/2\) 的概率执行该操作，\(tag\) 保持变为 \(1\)，故 \(dp_i=\dfrac{dp_i+1}{2}\)

• 对于Ⅲ类点，有 \(1/2\) 的概率不执行该操作，\(tag\) 保持不变，有 \(1/2\) 的概率执行该操作，如果 \(i\) 到根节点的路径上存在某个 \(tag\) 为 \(1\) 的点那么该节点的 \(tag\) 变为 \(1\)，否则 \(tag\) 保持为 \(0\)。故我们考虑引入一个新的量 \(f_i\) 表示当前状态下有多大概率存在 \(i\) 到根节点路径上的某个点 \(j\) 满足 \(tag_j=1\)，如果我们已经求出了 \(f_i\)，那么显然有 \(dp_i=\dfrac{dp_i+f_i}{2}\)。

• 对于其他节点，显然执行不执行该操作对该节点的 \(tag\) 没有影响，故 \(dp_i\) 保持不变。

注意到这三类节点的个数加起来是 \(\log n\) 级别的（因为Ⅰ类点 \(+\) Ⅱ类点个数是 \(\log n\) 级别的，而每个Ⅰ类点最多贡献 \(1\) 个Ⅲ类点），故直接计算 \(dp\) 是没问题的，于是问题转化为怎样求 \(f_i\)。

• 对于Ⅰ类点，有 \(1/2\) 的概率不执行该操作，概率保持不变，有 \(1/2\) 的概率执行该操作，它到根节点路径上所有节点的 \(tag\) 都会变为 \(0\)，故 \(f_i=\dfrac{f_i}{2}\)
• 对于Ⅱ类点，有 \(1/2\) 的概率不执行该操作，概率保持不变，有 \(1/2\) 的概率执行该操作，它自身的 \(tag\) 就变为了 \(1\)，故 \(f_i=\dfrac{f_i+1}{2}\)。
• 对于Ⅲ类点，不难发现操作本质实际上是将其到根节点路径上的 \(tag\) 转移到该节点上，故 \(f_i\) 保持不变。

对于不属于这三类节点的其他节点，我们又可将其分为两类——在Ⅲ类节点子树中的节点和在Ⅱ类节点子树中的节点：

• 在Ⅲ类节点子树中的节点，效仿计算Ⅲ类节点 \(f_i\) 的变化情况的过程可知这样的节点的 \(f\) 值保持不变。
• 在Ⅱ类节点子树中的节点，有 \(1/2\) 的概率不执行该操作，概率保持不变，有 \(1/2\) 的概率执行该操作，这样一来其到根节点的路径上一定存在某个节点（当前考虑的Ⅱ类节点）\(tag\) 为 \(1\)，故 \(f_i=\dfrac{f_i+1}{2}\)。

考虑每次操作维护一个懒标记 \(lz\) 表示当前区间中的节点进行了 \(lz\) 次 \(f_i=\leftarrow\dfrac{f_i+1}{2}\) 次操作，显然经过 \(lz\) 次操作后 \(f_i\) 会变为 \(\dfrac{f_i+2^{lz}-1}{2^{lz}}\)，故可以做到 \(\mathcal O(1)\) 下推懒标记。于是这题就做完了。

时间复杂度线对。

#include <bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define fill0(a) memset(a,0,sizeof(a))
#define fill1(a) memset(a,-1,sizeof(a))
#define fillbig(a) memset(a,63,sizeof(a))
#define pb push_back
#define ppb pop_back
#define mp make_pair
template<typename T1,typename T2> void chkmin(T1 &x,T2 y){if(x>y) x=y;}
template<typename T1,typename T2> void chkmax(T1 &x,T2 y){if(x<y) x=y;}
typedef pair<int,int> pii;
typedef long long ll;
typedef unsigned int u32;
typedef unsigned long long u64;
namespace fastio{
	#define FILE_SIZE 1<<23
	char rbuf[FILE_SIZE],*p1=rbuf,*p2=rbuf,wbuf[FILE_SIZE],*p3=wbuf;
	inline char getc(){return p1==p2&&(p2=(p1=rbuf)+fread(rbuf,1,FILE_SIZE,stdin),p1==p2)?-1:*p1++;}
	inline void putc(char x){(*p3++=x);}
	template<typename T> void read(T &x){
		x=0;char c=getchar();T neg=0;
		while(!isdigit(c)) neg|=!(c^'-'),c=getchar();
		while(isdigit(c)) x=(x<<3)+(x<<1)+(c^48),c=getchar();
		if(neg) x=(~x)+1;
	}
	template<typename T> void recursive_print(T x){if(!x) return;recursive_print(x/10);putc(x%10^48);}
	template<typename T> void print(T x){if(!x) putc('0');if(x<0) putc('-'),x=~x+1;recursive_print(x);}
	void print_final(){fwrite(wbuf,1,p3-wbuf,stdout);}
}
const int MAXN=1e5;
const int INV2=499122177;
const int MOD=998244353;
int n,qu,pw2[MAXN+5],pw2_1[MAXN+5],inv2[MAXN+5];
struct node{int l,r,dp,sdp,lz,sum;} s[MAXN*8+5];
void pushup(int k){s[k].sum=((s[k<<1].sum+s[k<<1|1].sum)%MOD+s[k].dp)%MOD;}
void pushdown(int k){
	s[k<<1].sdp=1ll*(s[k<<1].sdp+pw2[s[k].lz]-1)*inv2[s[k].lz]%MOD;
	s[k<<1|1].sdp=1ll*(s[k<<1|1].sdp+pw2[s[k].lz]-1)*inv2[s[k].lz]%MOD;
	s[k<<1].lz+=s[k].lz;s[k<<1|1].lz+=s[k].lz;s[k].lz=0;
}
void build(int k,int l,int r){
	s[k].l=l;s[k].r=r;if(l==r) return;
	int mid=l+r>>1;build(k<<1,l,mid);build(k<<1|1,mid+1,r);
}
void modify(int k,int l,int r){
	if(r<s[k].l||l>s[k].r){
		s[k].dp=1ll*(s[k].dp+s[k].sdp)*INV2%MOD;
		pushup(k);return;
	}
	if(l<=s[k].l&&s[k].r<=r){
		s[k].dp=1ll*(s[k].dp+1)*INV2%MOD;
		s[k].sdp=1ll*(s[k].sdp+1)*INV2%MOD;
		s[k].lz++;pushup(k);return;
	}
	s[k].dp=1ll*s[k].dp*INV2%MOD;s[k].sdp=1ll*s[k].sdp*INV2%MOD;
	pushdown(k);modify(k<<1,l,r);modify(k<<1|1,l,r);
	pushup(k);
}
void iterate(int k){
//	printf("%d %d %d %d %d\n",k,s[k].l,s[k].r,s[k].dp,s[k].sdp);
	if(s[k].l==s[k].r) return;pushdown(k);iterate(k<<1);iterate(k<<1|1);
}
int main(){
	scanf("%d%d",&n,&qu);int qq=0;
	pw2[0]=1;for(int i=1;i<=MAXN;i++) pw2[i]=pw2[i-1]*2%MOD;
	inv2[0]=1;for(int i=1;i<=MAXN;i++) inv2[i]=1ll*inv2[i-1]*INV2%MOD;
	build(1,1,n);
	while(qu--){
		int opt;scanf("%d",&opt);
		if(opt==1){int l,r;scanf("%d%d",&l,&r);modify(1,l,r);qq++;}
		else printf("%d\n",1ll*s[1].sum*pw2[qq]%MOD);
	}
	return 0;
}