脱壳入门----常见的寻找OEP的方法

一步直达法

所谓的一步直达法就是利用壳的特征。壳一般在执行完壳代码之后需要跳转到OEP处，而这个跳转指令一般是call ，jmp ，push retn类型的指令，而且因为壳代码所在的区段和OEP代码所在的区段一般属于不同的区段，所以我们可以通过搜索这些特殊指令的机器码并查看其跳转范围，如果跳转范围较大（也就是跨段跳转）则可以判断为此指令会跳到OEP处。

下面以UPX壳为例：

我们在OD中通过Crty + B来搜索二进制字串，call的机器码为E8，jmp的机器码为E9。这里我们搜索E9，通过Ctry + L来查看下一个机器码。

通过几次搜索之后我们找到了一条跳转到另一个区段的jmp指令，此指令就为对应的OEP跳转指令。

如果我们通过搜索jmp的机器码（E9）没有找到符合条件的跳转指令我们可以接着搜索call指令的机器码（E8）。

一步直达法的优点是简单，缺点是对一些强壳不好判断，因为一些强壳会采用jmp eax的方式跳转到oep中，而eax值我们是不能直接判断的，有的一些强壳还会对跳转到OEP的指令进行压缩，在执行此指令前才对其进行解压缩。这样我们通过直接搜索这些特定指令的机器码就很难判断是否为OEP跳转指令。

单步跟踪法

所谓的单步跟踪法就是从EP处开始F8单步向下跟踪，遇见向上跳转的指令不跳。这种方法实际是利用了壳代码的一般逻辑都是先解压缩原程序的各个区段和一些简单处理，然后最后跳转到OEP处。所以可以忽略前面的那些操作，直接去寻找OEP跳转的指令。这种方法也是存在一定的偶然性，对一些简单的壳能起到奇效。

模拟跟踪法

模拟跟踪法是利用OD的命令行插件，tc/toc命令是跟踪步进/步过 直到满足条件就暂停程序。因为OEP所在区段一般位于第一个区块处，而壳代码一般位于后几个区块中，因此我们可以利用tc/toc命令当eip小于壳代码所在的区块地址时说明程序跳转到了oep处。

下面我们用例子来演示一遍：

用OD加载程序后我们Alt+M查看内存，我们发现主模块的壳代码位于首地址为0x4F1000处。

我们在OD的命令行中输入 toc eip < 0x4F1000 后运行程序，程序会暂停到OEP处。

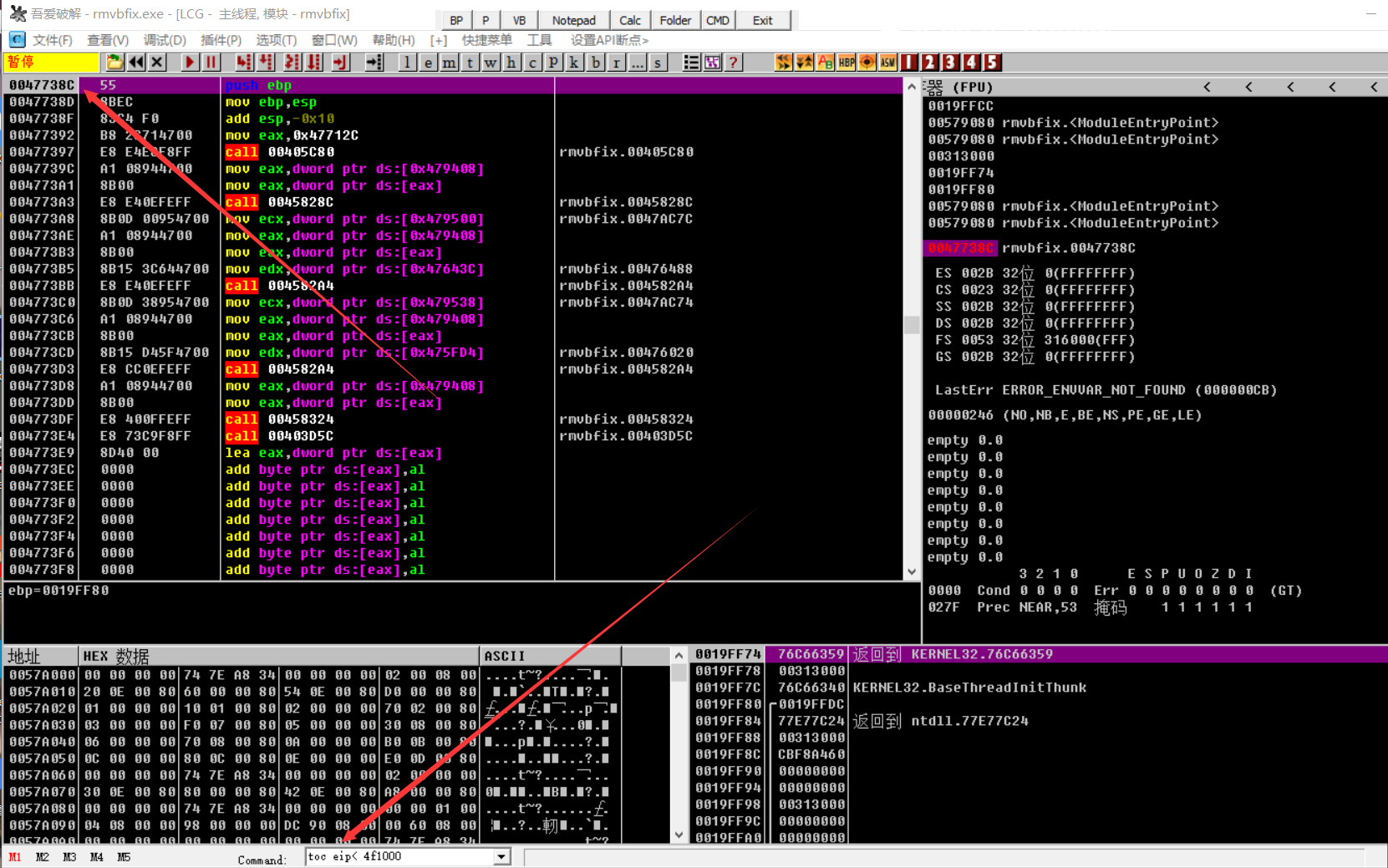
模拟跟踪法优点也是简单，缺点是耗时特别长，因为其在没执行完一条指令后都需要判断条件是否成立，所以程序运行很慢。而且如果壳代码和OEP在同一个区段中的话此方法就不适用了。（虽然这种情况很少，但不能保证没有）

SFX法

SFX法和模拟跟踪法十分相似，只不过SFX是OD本身提供的功能。

SFX法有两种方式，一种是通过判断块的形式看是否到达OEP处，另一种是通过判断字节的形式。显而易见块判断形式速度快但是准确度低，字节形式速度慢但是准确度高。我们在实际分析时结合具体情况选择合适的方式进行跟踪。

内存映像法

内存映像法就是通过对加载到内存中的程序下内存断点来寻找OEP，因为加壳程序在解压缩各个区段后会跳转到OEP执行此处的代码，所以我们可以通过先对OEP所在的区块设置内存写入断点，待此区段解压缩完成后我们再在此区块上设置内存访问断点。这样当程序执行到OEP处时就会暂停。

ESP定律法

ESP定律是利用堆栈平衡，一般壳代码在执行的时候回保存寄存器环境，在跳转到OEP处的时候再恢复环境。我们可以利用此特点在执行完push指令保存环境后，对堆栈设置硬件访问断点或内存访问断点。这样在跳转到OEP前其会执行pop指令，程序就会暂停我们就可以单步向下跟踪寻找OEP跳转指令。

最后一次异常法

有的加壳程序会在执行壳代码的时候设置很多异常来干扰脱壳破解者，其会在各个异常的异常处理程序中检测断点以及进行反调试。所以我们如果还用esp定律，内存映像等下断点的方法就会失效。我们需要将这些异常执行完之后在采取以上办法。最后一次异常法就是寻找到程序最后一次异常发生的指令，当最后一次异常执行后我们在采取常规方法寻找OEP。

利用应用程序调用的第一个API

通过对应用程序调用的第一个API下断点来到达OEP附近，从而进一步寻找到OEP。

例如GetVersion，GetModuleHandle等。

利用不同编译器编译程序入口特征码定位OEP

如果熟悉各个编译器编译程序入口点代码的特征就可以通过此方法来快速到达OEP处，我们可以在各个区块解压缩后通过搜索特定编译器程序入口点代码的特征码来到达OEP处。