力扣7(java)-整数反转（中等）

题目：

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−2³¹,  2³¹ − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

输入：x = 12331
输出：321
示例 2：

输入：x = -123
输出：-321
示例 3：

输入：x = 120
输出：21
示例 4：

输入：x = 0
输出：0

提示：

-2³¹ <= x <= 2³¹ - 1

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/reverse-integer
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题思路：

数学思维：

最大值与最小值：-2³¹ =  -2147483648，2³¹-1 = 2147483647

数学方法取末尾数字，以及将末尾数字推入反转数中：

//弹出x的末尾数字
digit = x % 10
x / = 10

//将数字digit推入rev末尾
rev = rev * 10 + digit

举例：

1.循环判断的条件：由于x可为正也可为负，不断的将 x /10,最后都会变成0，故循环判断条件应该为while( x != 0);

2.判断溢出：提前判断

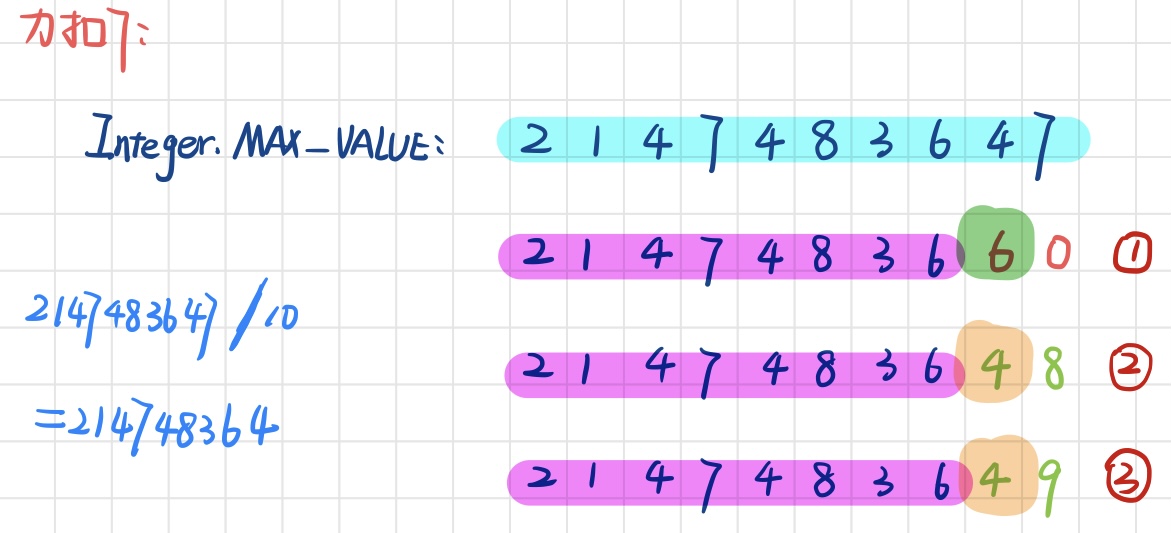
最大数：在最大数的倒数第二位（最大数的1/10）的时候就需要进行判断

• 如果比这个数大，后面就不需要进行判断，加任何数都会溢出，图中①；
• 如果等于这个数，就需要跟最大数的末尾数字7进行比较，如果大于7，会溢出，图中②③。

最小数：同样如此，在最小数的倒数第二位（最小数的1/10）的时候就需要进行判断

• 如果比这个数小，后面就不需要进行判断，加任何数都会溢出，图中①；
• 如果等于这个数，就需要跟最大数的末尾数字8进行比较，如果大于8,(加上前面的负号就越小)，会溢出，图中②。

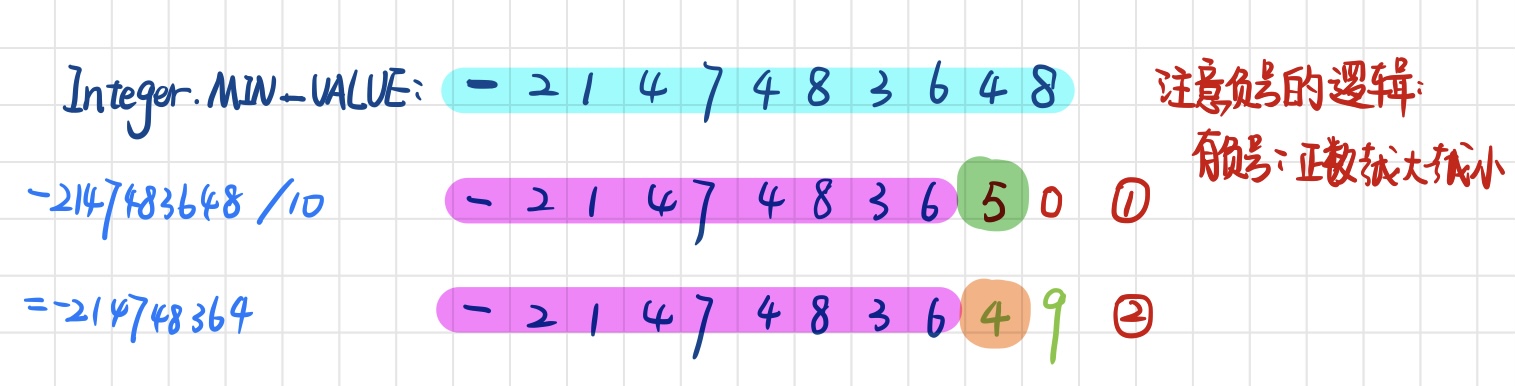
代码：

 1 class Solution {
 2     public int reverse(int x) {
 3         int rev = 0;
 4         //判断是否溢出
 5         while(x != 0){
 6             //计算末尾数字
 7             int digit = x % 10;
 8             if(rev > Integer.MAX_VALUE / 10 || (rev == Integer.MAX_VALUE / 10 && digit > 7)){
 9                 return 0;
10             }
11             if(rev < Integer.MIN_VALUE / 10 || (rev == Integer.MIN_VALUE / 10 && digit < -8)){
12                 return 0;
13             }
14             //将末尾数字放入反转数字的末尾
15             rev = rev * 10 + digit;
16             x /= 10;
17         }
18         return rev;
19     }
20 }

 小知识：

做这道题的时候，我发现我不会数学取余了，搜索博客整理一下java中取余的规则：

1. 负数 % 负数 = 结果为负

2. 负数 % 正数 =  结果为负

3. 正数 % 负数 = 结果为正

总结：计算时不管正负号，全部按照正数来计算，最终的正负号由分子来决定，与分子的正负号相同。