强化学习基础篇[2]：SARSA、Q-learning算法简介、应用举例、优缺点分析

强化学习基础篇[2]：SARSA、Q-learning算法简介、应用举例、优缺点分析

1.SARSA

SARSA（State-Action-Reward-State-Action）是一个学习马尔可夫决策过程策略的算法，通常应用于机器学习和强化学习学习领域中。它由Rummery 和 Niranjan在技术论文“Modified Connectionist Q-Learning（MCQL）” 中介绍了这个算法，并且由Rich Sutton在注脚处提到了SARSA这个别名。

State-Action-Reward-State-Action这个名称清楚地反应了其学习更新函数依赖的5个值，分别是当前状态S1，当前状态选中的动作A1，获得的奖励Reward，S1状态下执行A1后取得的状态S2及S2状态下将会执行的动作A2。我们取这5个值的首字母串起来可以得出一个词SARSA。

1.1基础概念

算法的核心思想可以简化为：

$$

Q(S_{t},A_{t})=Q(S_{t},A_{t})+\alpha[R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_{t},A_{t})]

$$

其中 $Q(S_{t+1},A_{t+1})$ 是下一时刻的状态和实际采取的行动对应的 Q 值，$Q(S_{t},A_{t})$ 是当前时刻的状态和实际采取的形同对应的Q值。折扣因子$\gamma$的取值范围是 [ 0 , 1 ]，其本质是一个衰减值，如果gamma更接近0，agent趋向于只考虑瞬时奖励值，反之如果更接近1，则agent为延迟奖励赋予更大的权重，更侧重于延迟奖励；奖励值$R_{t+1}$为t+1时刻得到的奖励值。$\alpha$为是学习率。

1.2应用举例

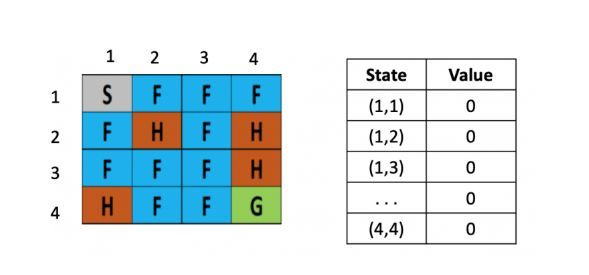
将一个结冰的湖看成是一个4×4的方格，每个格子可以是起始块（S），目标块（G）、冻结块（F）或者危险块（H），目标是通过上下左右的移动，找出能最快从起始块到目标块的最短路径来，同时避免走到危险块上，（走到危险块就意味着游戏结束）为了引入随机性的影响，还可以假设有风吹过，会随机的让你向一个方向漂移。

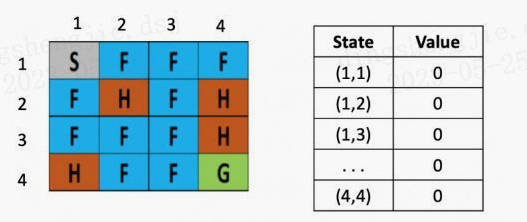
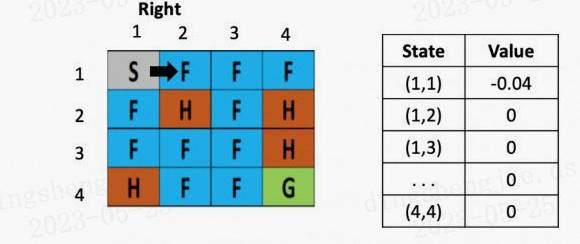
图1: 初始化

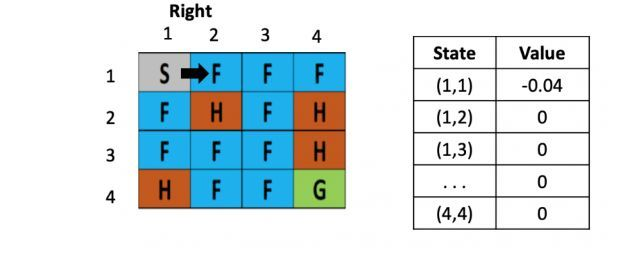
左图是每个位置对应的Q value的表，最初都是0，一开始的策略就是随机生成的，假定第一步是向右，那根据上文公式，假定学习率是$\alpha$是 0.1，折现率$\gamma$是0.5，而每走一步，会带来-0.4的奖励，那么（1.2）的Q value就是 0 + 0.1 ×[ -0.4 + 0.5× (0)-0] = -0.04，为了简化问题，此处这里没有假设湖面有风。

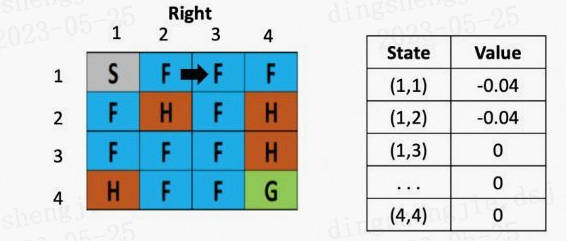
图2: 走一步

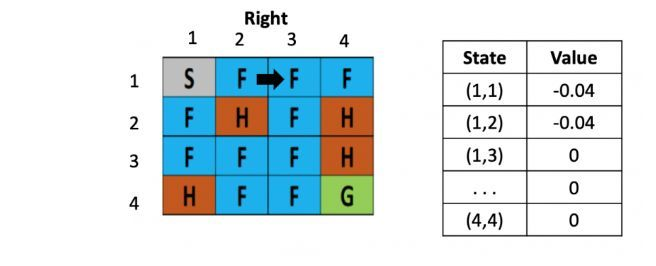
假设之后又接着往右走了一步，用类似的方法更新（1，3）的Q value了，得到（1.3）的Q value还为-0.04

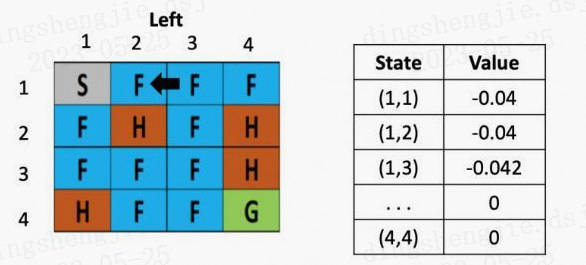
图3: 走一步

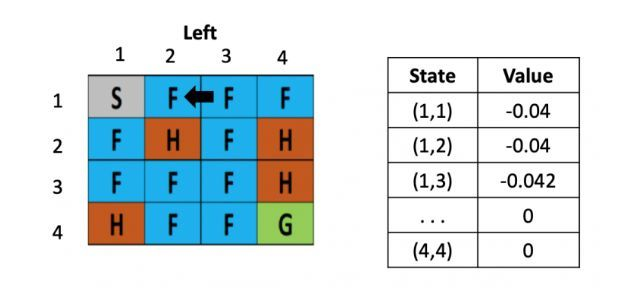
等到了下个时刻，骰子告诉我们要往左走，此时就需要更新（1，2）的Q-value，计算式为：V(s) = 0 +0.1× [ -0.4 + 0.5× (-0.04)-0) ]

图4: 走一步

从这里，智能体就能学到先向右在向左不是一个好的策略，会浪费时间，依次类推，不断根据之前的状态更新左边的Q table，直到目标达成或游戏结束。

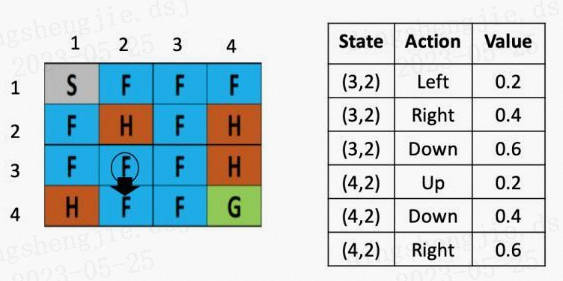
图5: 走一步

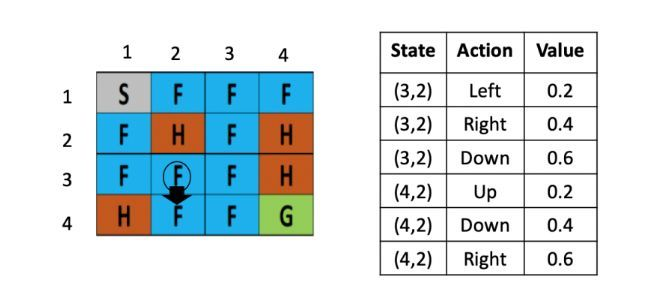
假设现在智能体到达了如图5所示的位置，现在要做的是根据公式，更新（3，2）这里的Q value，由于向下走的Q-value最低，假定学习率是0.1，折现率是0.5，那么（3，2）这个点向下走这个策略的更新后的Q value就是，Sarsa会随机选一个action,比如这里选择的是(Q(4,2),down)：

$$ Q( (3,2) down) = Q( (3,2) down ) + 0.1× ( -0.4 + 0.5 × (Q( (4,2) down) )- Q( (3,2), down））$$

$$ Q( (3,2), down) = 0.6 + 0.1× ( -0.4 + 0.5 × 0.4 – 0.6)=0.52 $$

1.3 优缺点

SARSA 算法经常与Q-learning 算法作比较，以便探索出两种算法分别适用的情况。它们互有利弊。

与SARSA相比，Q-learning具有以下优点和缺点：

• Q-learning直接学习最优策略，而SARSA在探索时学会了近乎最优的策略。
• Q-learning具有比SARSA更高的每样本方差，并且可能因此产生收敛问题。当通过Q-learning训练神经网络时，这会成为一个问题。
• SARSA在接近收敛时，允许对探索性的行动进行可能的惩罚，而Q-learning会直接忽略，这使得SARSA算法更加保守。如果存在接近最佳路径的大量负面报酬的风险，Q-learning将倾向于在探索时触发奖励，而SARSA将倾向于避免危险的最佳路径并且仅在探索参数减少时慢慢学会使用它。

如果是在模拟中或在低成本和快速迭代的环境中训练代理，那么由于第一点（直接学习最优策略），Q-learning是一个不错的选择。 如果代理是在线学习，并且注重学习期间获得的奖励，那么SARSA算法更加适用。

2.Q-learning

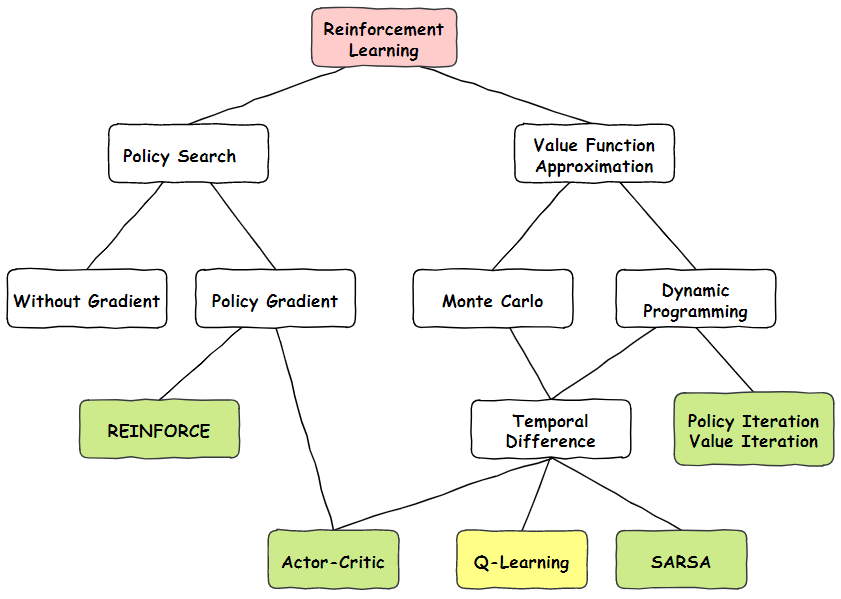
首先我们看一下上图Q-learning在整个强化学习的位置，Q-Learning是属于值函数近似算法中，蒙特卡洛方法和时间差分法相结合的算法。它在1989年被Watkins提出，可以说一出生就给强化学习带来了重要的突破。

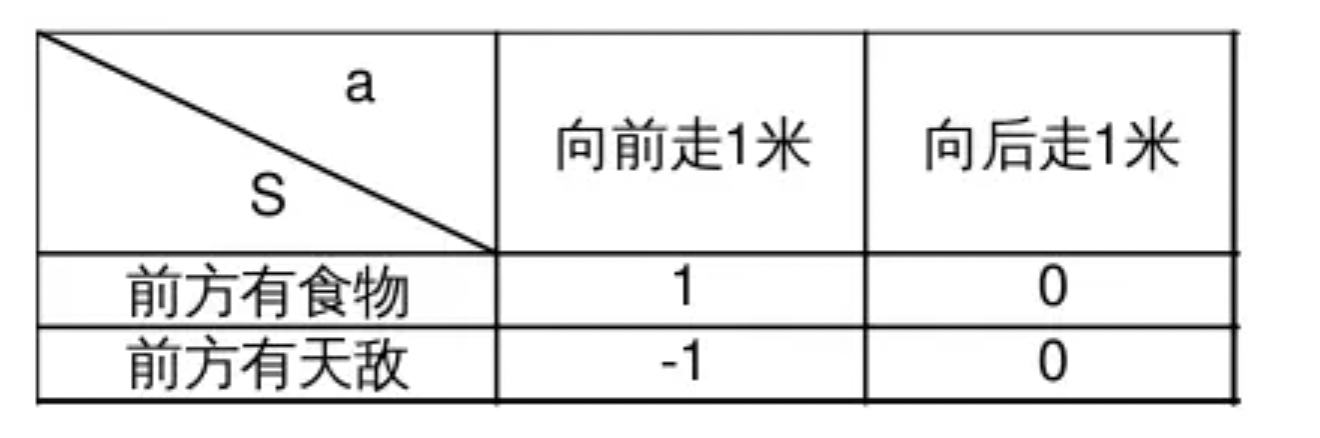
Q-Learning假设可能出现的动作a和状态S是有限多，这时a和S的全部组合也是有限多个，并且引入价值量Q表示智能体认为做出某个a时所能够获得的利益。在这种假设下，智能体收到S，应该做出怎样的a，取决于选择哪一个a可以产生最大的Q。下面的表格显示了动物在面对环境的不同状态时做出的a对应着怎样的Q，这里为了简单说明只分别列举了2种S和a：

显然，如果此时S="前方有食物"，选择a="向前走1米"，得到的利益Q="1" 显然比选择a="向后走1米" 的q="0"要大，所以这时应该选择向前走；相对的前方如果有天敌，往前走显然没有任何利益，这时选择最大的利益就要向后走。这种表格在Q-Learning中被称为Q表，表中的S和a需要事先确定，表格主体的数据——q在初始化的时候被随机设置，在后续通过训练得到矫正。

2.1 基础概念

Q-Learning的训练过程是Q表的Q值逐渐调整的过程，其核心是根据已经知道的Q值，当前选择的行动a作用于环境获得的回报R和下一轮$S_{t+1}$对应可以获得的最大利益Q，总共三个量进行加权求和算出新的Q值，来更新Q表：

$$

Q(S_{t},A_{t})=Q(S_{t},A_{t})+\alpha[R_{t+1}+\gamma \mathop{max}{a} Q(S,a)-Q(S_{t},A_{t})]

$$

其中 $Q(S_{t+1}, a)$ 是在 $t+1$ 时刻的状态和采取的行动（并不是实际行动，所以公式采用了所有可能采取行动的Q的最大值）对应的 Q 值，$Q(S_{t},A_{t})$ 是当前时刻的状态和实际采取的形同对应的Q值。折扣因子$\gamma$的取值范围是 [ 0 , 1 ]，其本质是一个衰减值，如果gamma更接近0，agent趋向于只考虑瞬时奖励值，反之如果更接近1，则agent为延迟奖励赋予更大的权重，更侧重于延迟奖励；奖励值$R_{t+1}$为t+1时刻得到的奖励值。$\alpha$为是学习率。

这里动作价值Q函数的目标就是逼近最优的$q$ $q=R_{t+1}+\gamma \mathop{max}{a} Q(S,a)$，并且轨迹的行动策略与最终的$q$是无关的。后面中括号的加和式表示的是 $q$的贝尔曼最优方程近似形式。

2.2 应用举例

将一个结冰的湖看成是一个4×4的方格，每个格子可以是起始块（S），目标块（G）、冻结块（F）或者危险块（H），目标是通过上下左右的移动，找出能最快从起始块到目标块的最短路径来，同时避免走到危险块上，（走到危险块就意味着游戏结束）为了引入随机性的影响，还可以假设有风吹过，会随机的让你向一个方向漂移。

图1: 初始化

左图是每个位置对应的Q value的表，最初都是0，一开始的策略就是随机生成的，假定第一步是向右，那根据上文公式，假定学习率是$\alpha$是 0.1，折现率$\gamma$是0.5，而每走一步，会带来-0.4的奖励，那么（1.2）的Q value就是 0 + 0.1 ×[ -0.4 + 0.5× (0)-0] = -0.04，为了简化问题，此处这里没有假设湖面有风。

图2: 走一步

假设之后又接着往右走了一步，用类似的方法更新（1，3）的Q value了，得到（1.3）的Q value还为-0.04

图3: 走一步

等到了下个时刻，骰子告诉我们要往左走，此时就需要更新（1，2）的Q-value，计算式为：V(s) = 0 +0.1× [ -0.4 + 0.5× (-0.04)-0) ]

图4: 走一步

从这里，智能体就能学到先向右在向左不是一个好的策略，会浪费时间，依次类推，不断根据之前的状态更新左边的Q table，直到目标达成或游戏结束。

图5: 走一步

假设现在智能体到达了如图5所示的位置，现在要做的是根据公式，更新（3，2）这里的Q value，由于向下走的Q-value最低，假定学习率是0.1，折现率是0.5，那么（3，2）这个点向下走这个策略的更新后的Q value就是：

$$ Q( (3,2) down) = Q( (3,2) down ) + 0.1× ( -0.4 + 0.5 × max [Q( (4,2) action) ]- Q( (3,2), down））$$

$$ Q( (3,2), down) = 0.6 + 0.1× ( -0.4 + 0.5 × max [0.2, 0.4, 0.6] – 0.6)=0.53 $$

2.3 优缺点

Q-Learning算法有一些缺点，比如状态和动作都假设是离散且有限的，对于复杂的情况处理起来会很麻烦；智能体的决策只依赖当前环境的状态，所以如果状态之间存在时序关联那么学习的效果就不佳。

更多文章请关注公重号：汀丶人工智能