【matlab混沌理论】1.4.双摆杆的不同参数模型
双摆杆运动模型。初始条件的微小差异,会导致千差万别的运动现象,这是混沌理论重要体现。主要考虑初始条件有两摆杆长度、质量、初始摆杆角度、重力加速度。
input:
% 参数定义
L1 = 1; % 第一根摆长
L2 = 0.5; % 第二根摆长
m1 = 1; % 第一根摆质量
m2 = 0.5; % 第二根摆质量
g = 9.81; % 重力加速度 % 初始状态定义
theta1 = pi/6; % 第一根摆角度
theta2 = 0; % 第二根摆角度
dtheta1 = 0; % 第一根摆角速度
dtheta2 = 0; % 第二根摆角速度 % 动画绘制
tspan = [0 30]; % 时间跨度
y0 = [theta1 dtheta1 theta2 dtheta2]; % 初始状态向量
[t, y] = ode45(@(t,y) pendulum2(t, y, L1, L2, m1, m2, g), tspan, y0); % 解微分方程 x1 = L1*sin(y(:,1)); % 第一根摆x坐标
y1 = -L1*cos(y(:,1)); % 第一根摆y坐标
x2 = L1*sin(y(:,1)) + L2*sin(y(:,3)); % 第二根摆x坐标
y2 = -L1*cos(y(:,1)) - L2*cos(y(:,3)); % 第二根摆y坐标 set(gcf, 'renderer', 'painters');
axis equal; % x、y轴比例相等
axis([-1.5*(L1+L2) 1.5*(L1+L2) -1.5*(L1+L2) 1.5]); % 设置坐标轴范围
hold on; x1_trace = zeros(length(t), 1); % 第一个摆的摆顶端x坐标
y1_trace = zeros(length(t), 1); % 第一个摆的摆顶端y坐标
x2_trace = zeros(length(t), 1); % 第二个摆的摆顶端x坐标
y2_trace = zeros(length(t), 1); % 第二个摆的摆顶端y坐标 % 绘制双摆动画,同时画出摆顶端轨迹连线
for k = 1:length(t)-1
plot([0 x1(k) x2(k)], [0 y1(k) y2(k)], 'linewidth', 0.5); % 绘制双摆图形
plot(x2(1:k), y2(1:k), '.', 'color', [0.8 0.05 0.1], 'markersize', 10); % 绘制尾迹
x1_trace(k+1) = L1*sin(y(k+1,1));
y1_trace(k+1) = -L1*cos(y(k+1,1));
x2_trace(k+1) = x1_trace(k+1) + L2*sin(y(k+1,3));
y2_trace(k+1) = y1_trace(k+1) - L2*cos(y(k+1,3));
plot([x1_trace(k) x1_trace(k+1)], [y1_trace(k) y1_trace(k+1)], 'linewidth', 1, 'color', 'blue'); % 第一个摆的轨迹线
plot([x2_trace(k) x2_trace(k+1)], [y2_trace(k) y2_trace(k+1)], 'linewidth', 1, 'color', 'green'); % 第二个摆的轨迹线
drawnow; % 实时显示
end % 微分方程定义
function dydt = pendulum2(t, y, L1, L2, m1, m2, g)
dydt = zeros(4,1); % 向量拆分为各个分量
theta1 = y(1);
dtheta1 = y(2);
theta2 = y(3);
dtheta2 = y(4); % 运动方程
% 第一个摆的力
F1 = -m1*L1*dtheta1^2*sin(theta1) - m1*g*cos(theta1)*sin(theta1);
% 第二个摆的力
F2 = -m2*(L1*dtheta1^2*sin(theta1) + L2*dtheta2^2*sin(theta2)) - m2*g*cos(theta2)*sin(theta2);
% 坐标加速度
d2theta1 = (F1 + m1*g*sin(theta1)*cos(theta1) + F2*cos(theta1-theta2))/(m1*L1^2 + m2*L1^2 - m2*L1*L2*cos(theta1-theta2));
d2theta2 = (F2*cos(theta1-theta2) + (m1+m2)*g*sin(theta1) + L1*dtheta1^2*sin(theta1)*cos(theta1-theta2) - (m1+m2)*L2*dtheta2^2*sin(theta1-theta2))/(L2^2*m2 + (m1+m2)*L1^2 - 2*L1*L2*m2*cos(theta1-theta2)); dydt(1) = dtheta1; % 第一个摆角速度
dydt(2) = d2theta1; % 第一个摆角加速度
dydt(3) = dtheta2; % 第二个摆角速度
dydt(4) = d2theta2; % 第二个摆角加速度
end
output:
初始条件:L1 = 1;L2 = 0.5;m1 = 1;m2 = 0.5;theta1 = pi/6;theta2 = 0;dtheta1 = 0;dtheta2 = 0;
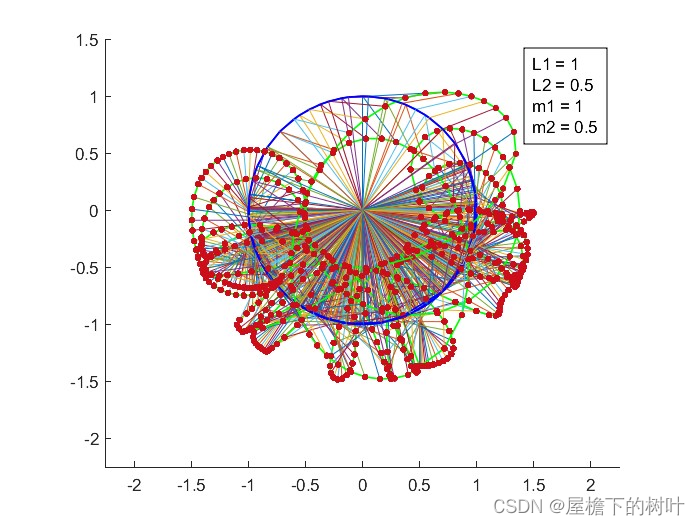
output:
初始条件:第二摆杆长度是第一摆杆的一半,其余变量也不同。
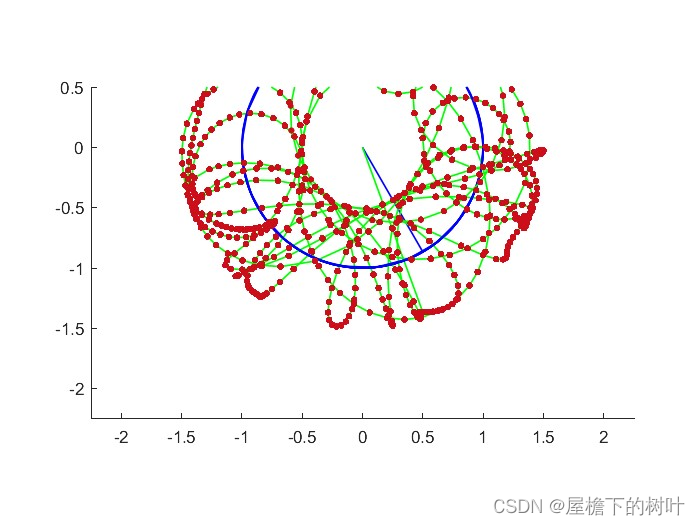
output:
初始条件:第一摆杆长度、质量等于第一摆杆的,初始摆角不同。
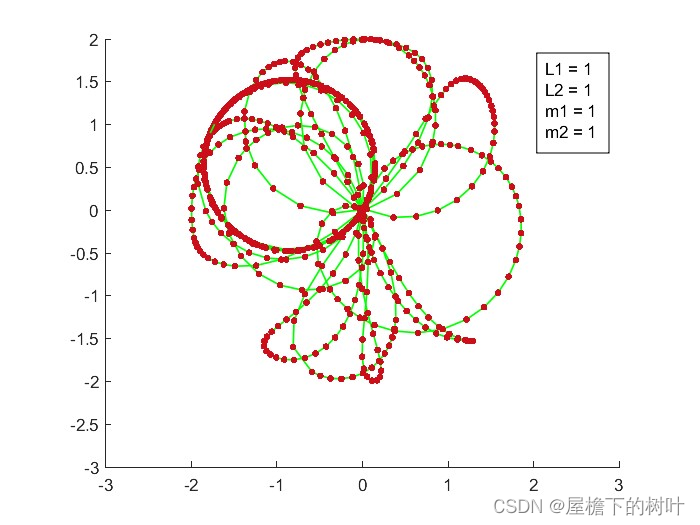
【matlab混沌理论】1.4.双摆杆的不同参数模型的更多相关文章
- 混沌理论(Chaos theory)和非线性系统
混沌理论(Chaos theory)是关于非线性系统在一定参数条件下展现分岔(bifurcation).周期运动与非周期运动相互纠缠,以至于通向某种非周期有序运动的理论.在耗散系统和保守系统中,混沌运 ...
- 如何实现Linux+Windows双系统启动
设置你的计算机根据需要启动 Windows 10 或 Ubuntu 18.04. 尽管 Linux 是一个有着广泛的硬件和软件支持的操作系统,但事实上有时你仍需要使用 Windows,也许是因为有些不 ...
- 混沌数学之Chua's circuit(蔡氏电路)
蔡氏电路(英语:Chua's circuit),一种简单的非线性电子电路设计,它可以表现出标准的混沌理论行为.在1983年,由蔡少棠教授发表,当时他正在日本早稻田大学担任访问学者[1].这个电路的制作 ...
- 《零起点,python大数据与量化交易》
<零起点,python大数据与量化交易>,这应该是国内第一部,关于python量化交易的书籍. 有出版社约稿,写本量化交易与大数据的书籍,因为好几年没写书了,再加上近期"前海智库 ...
- 【转】漫谈ANN(2):BP神经网络
上一次我们讲了M-P模型,它实际上就是对单个神经元的一种建模,还不足以模拟人脑神经系统的功能.由这些人工神经元构建出来的网络,才能够具有学习.联想.记忆和模式识别的能力.BP网络就是一种简单的人工神经 ...
- 神经网络4_BP神经网络
sklearn实战-乳腺癌细胞数据挖掘(博客主亲自录制视频教程) https://study.163.com/course/introduction.htm?courseId=1005269003&a ...
- 止损+TS
单策略单品种单策略多品种多策略单品种和加仓多策略多品种静态仓位和动态仓位 金肯特钠(kingKeltner)布林强盗(BollingerBandit)动态突破(DynamicBreakOutII)恒温 ...
- [原创]AHA大会回顾
AHA大会回顾 缘起 AHA之前参加了Daniel的培训,了解到AHA大会,觉得很高大上,开始有些心动.考虑到是工作时间,而且是外地,所以也就停留在心动层面了.之后与伯薇和四正吃饭,听说他们要去参加这 ...
- 对GBK的理解(内附全部字符编码列表):扩充的2万汉字低字节的高位不等于1,而且还剩许多编码空间没有利用
各种编码查询表:http://bm.kdd.cc/ 由于GB 2312-80只收录6763个汉字,有不少汉字,如部分在GB 2312-80推出以后才简化的汉字(如“啰”),部分人名用字(如中国前总理朱 ...
- 汉字与区位码互转(天天使用的String存储的是内码),几个常见汉字编码,附有读书笔记
汉=BABA(内码)=-A0A0=2626(区位码)字=D7D6(内码)=-A0A0=5554(区位码) 各种编码查询表:http://bm.kdd.cc/ “啊”字是GB2312之中的第一个汉字,会 ...
随机推荐
- 问题排查:nginx的反向代理感觉失效了一样
背景 最近,负责基础设施的同事,要对一批测试环境机器进行回收,回收就涉及到应用迁移,问题是整个过程一团乱.比如服务器A上一堆应用要调用服务器B上一堆服务,结果服务器B被回收了,然后服务器A上一堆应用报 ...
- Mybatis插件功能
1 插件的作用 在Mybatis执行SQL的生命周期中,会使用插件进行埋点,主要包括Executor.StatementHandler.ParameterHandler和ResultSetHandle ...
- Linux 内核设备树时钟绑定
这种绑定依然处于开发中,并且基于 benh[1] 的一些实验性工作. 时钟信号源可以由设备树中的任何节点表示.这些节点被指定为时钟提供者.时钟消费者节点使用 phandle 和时钟指示符对将时钟提供者 ...
- C# 异步执行操作
为了方便测试异步,先加个计时 计时相关(可以直接跳过该部分) //开始计时 Stopwatch stopwatch = new Stopwatch(); stopwatch.Start(); // 停 ...
- vscod 配置 morkdown 快捷键
vscod 配置 morkdown 快捷键 1.首先在根目录添加.vscode 文件夹 ️1.1 新建一个 settings.json 文件 { "[markdown]": { & ...
- 关于TCP 四次挥手过程中的reset包问题
数据包过程 TCP状态机转换过程 客户端在接受到第32个数据包之后,应该发送1个对FIN的ACK数据包,然而客户端缺直接连续发送了3个Rest数据包36~38,客户端并未进入time wait阶段,直 ...
- Hadoop - WARN util.NativeCodeLoader: Unable to load native-hadoop library for your platform...
Hadoop - WARN util.NativeCodeLoader: Unable to load native-hadoop library for your platform... 配置完ha ...
- mount时候遇到写保护,将以只读方式挂载
mount时候遇到写保护,将以只读方式挂载 遇到 mount: 未知的文件系统类型"(null)" [root@localhost ~]# mount /dev/sdb /mnt/ ...
- Python基础概要(一天快速入门)
文章目录 一 编程与编程语言 二 编程语言分类 三 主流编程语言介绍 四 Python介绍 五 安装python解释器 六 第一个python程序 七 变量 八 用户与程序交互 九 基本数据类型 十 ...
- python第2~5章 code
02基本语法 print('he\aaa\aaa') # 这是一个打印语句,请你看见了不要慌张# 这是一个注释# 注释会被解释器所忽略# print(123+456) 这行代码被注释了,将不会执行pr ...
