神经网络入门篇：详解随机初始化（Random+Initialization）

当训练神经网络时，权重随机初始化是很重要的。对于逻辑回归，把权重初始化为0当然也是可以的。但是对于一个神经网络，如果把权重或者参数都初始化为0，那么梯度下降将不会起作用。

来看看这是为什么。

有两个输入特征，\(n^{[0]} = 2\)，2个隐藏层单元\(n^{[1]}\)就等于2。

因此与一个隐藏层相关的矩阵，或者说\(W^{[1]}\)是2*2的矩阵，假设把它初始化为0的2*2矩阵，\(b^{[1]}\)也等于 \([0\;0]^T\)，把偏置项\(b\)初始化为0是合理的，但是把\(w\)初始化为0就有问题了。

那这个问题如果按照这样初始化的话，总是会发现\(a_{1}^{[1]}\) 和 \(a_{2}^{[1]}\)相等，这个激活单元和这个激活单元就会一样。因为两个隐含单元计算同样的函数，当做反向传播计算时，这会导致\(\text{dz}_{1}^{[1]}\) 和 \(\text{dz}_{2}^{[1]}\)也会一样，对称这些隐含单元会初始化得一样，这样输出的权值也会一模一样，由此\(W^{[2]}\)等于\([0\;0]\)；

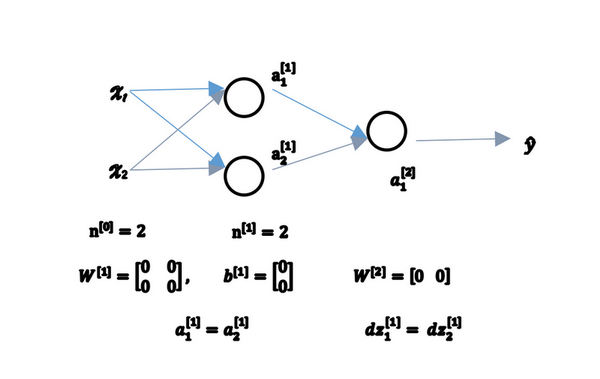
图1.11.1

但是如果这样初始化这个神经网络，那么这两个隐含单元就会完全一样，因此他们完全对称，也就意味着计算同样的函数，并且肯定的是最终经过每次训练的迭代，这两个隐含单元仍然是同一个函数，令人困惑。\(dW\)会是一个这样的矩阵，每一行有同样的值因此做权重更新把权重\(W^{[1]}\implies{W^{[1]}-adW}\)每次迭代后的\(W^{[1]}\)，第一行等于第二行。

由此可以推导，如果把权重都初始化为0，那么由于隐含单元开始计算同一个函数，所有的隐含单元就会对输出单元有同样的影响。一次迭代后同样的表达式结果仍然是相同的，即隐含单元仍是对称的。通过推导，两次、三次、无论多少次迭代，不管训练网络多长时间，隐含单元仍然计算的是同样的函数。因此这种情况下超过1个隐含单元也没什么意义，因为他们计算同样的东西。当然更大的网络，比如有3个特征，还有相当多的隐含单元。

如果要初始化成0，由于所有的隐含单元都是对称的，无论运行梯度下降多久，他们一直计算同样的函数。这没有任何帮助，因为想要两个不同的隐含单元计算不同的函数，这个问题的解决方法就是随机初始化参数。应该这么做：把\(W^{[1]}\)设为np.random.randn(2,2)(生成高斯分布)，通常再乘上一个小的数，比如0.01，这样把它初始化为很小的随机数。然后\(b\)没有这个对称的问题（叫做symmetry breaking problem），所以可以把 \(b\) 初始化为0，因为只要随机初始化\(W\)就有不同的隐含单元计算不同的东西，因此不会有symmetry breaking问题了。相似的，对于\(W^{[2]}\)可以随机初始化，\(b^{[2]}\)可以初始化为0。

\(W^{[1]} = np.random.randn(2,2)\;*\;0.01\;,\;b^{[1]} = np.zeros((2,1))\)

\(W^{[2]} = np.random.randn(2,2)\;*\;0.01\;,\;b^{[2]} = 0\)

也许会疑惑，这个常数从哪里来，为什么是0.01，而不是100或者1000。通常倾向于初始化为很小的随机数。因为如果用tanh或者sigmoid激活函数，或者说只在输出层有一个Sigmoid，如果（数值）波动太大，当计算激活值时\(z^{[1]} = W^{[1]}x + b^{[1]}\;,\;a^{[1]} = \sigma(z^{[1]})=g^{[1]}(z^{[1]})\)如果\(W\)很大，\(z\)就会很大或者很小，因此这种情况下很可能停在tanh/sigmoid函数的平坦的地方(见图3.8.2)，这些地方梯度很小也就意味着梯度下降会很慢，因此学习也就很慢。

回顾一下：如果\(w\)很大，那么很可能最终停在（甚至在训练刚刚开始的时候）\(z\)很大的值，这会造成tanh/Sigmoid激活函数饱和在龟速的学习上，如果没有sigmoid/tanh激活函数在整个的神经网络里，就不成问题。但如果做二分类并且的输出单元是Sigmoid函数，那么不会想让初始参数太大，因此这就是为什么乘上0.01或者其他一些小数是合理的尝试。对于\(w^{[2]}\)一样，就是np.random.randn((1,2))，猜会是乘以0.01。

事实上有时有比0.01更好的常数，当训练一个只有一层隐藏层的网络时（这是相对浅的神经网络，没有太多的隐藏层），设为0.01可能也可以。但当训练一个非常非常深的神经网络，可能要试试0.01以外的常数。无论如何它通常都会是个相对小的数。

好了，看完神经网络入门篇。就已经知道如何建立一个一层的神经网络了，初始化参数，用前向传播预测，还有计算导数，结合反向传播用在梯度下降中。