SVD/SVD++实现推荐算法

奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不仅可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。

我们首先回顾下特征值和特征向量的定义如下：

                                                                    Ax=λx

其中A是一个n×n的矩阵，x是一个n维向量，则我们说λ是矩阵A的一个特征值，而x是矩阵A的特征值λ所对应的特征向量。

　　求出特征值和特征向量有什么好处呢？ 我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值λ1≤λ2≤...≤λn,以及这n个特征值所对应的特征向量{w1,w2,...wn}，那么矩阵A就可以用下式的特征分解表示：

A=WΣW⁻¹

其中W是这n个特征向量所张成的n×n维矩阵，而Σ为这n个特征值为主对角线的n×n维矩阵。

　　一般我们会把W的这n个特征向量标准化，即满足||wi||2=1, 或者说w^T_iw_i=1，此时W的n个特征向量为标准正交基，满足W^TW=I，即W^T=W−1, 也就是说W为酉矩阵。

　　　　这样我们的特征分解表达式可以写成A=WΣW^T

　　　　注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

SVD的定义

　　　　SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个m×nm×n的矩阵，那么我们定义矩阵A的SVD为：

                                                       A=UΣV^T   

　　　　其中U是一个m×m的矩阵，Σ是一个m×n的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个n×n的矩阵。U和V都是酉矩阵，即满足U^TU=I,V^TV=I。下图可以很形象的看出上面SVD的定义：

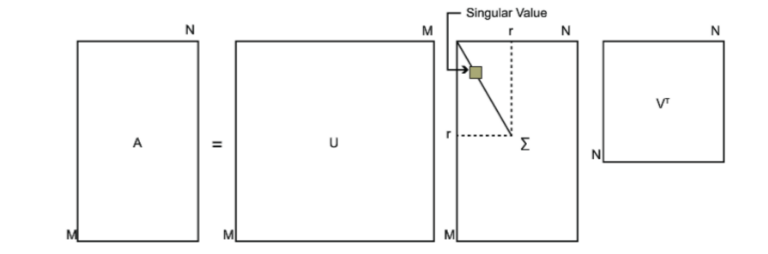
　　　　那么我们如何求出SVD分解后的U,Σ,V这三个矩阵呢？

　　　　如果我们将A的转置和A做矩阵乘法，那么会得到n×nn×n的一个方阵ATA。既然ATA是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

                                                                    (A^TA)vi=λivi

　　　　这样我们就可以得到矩阵ATA的n个特征值和对应的n个特征向量v了。将ATA的所有特征向量张成一个n×n的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

　　　　如果我们将A和A的转置做矩阵乘法，那么会得到m×m的一个方阵AAT。既然AAT是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：

                                                               (AA^T)ui=λiui

　　　　这样我们就可以得到矩阵AAT的m个特征值和对应的m个特征向量u了。将AAT的所有特征向量张成一个m×m的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

　　　　U和V我们都求出来了，现在就剩下奇异值矩阵Σ没有求出了。由于Σ除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值σ就可以了。

　　　　我们注意到:

                                                              A=UΣV^T⇒AV=UΣV^TV⇒AV=UΣ⇒Av_i=σ_iu_i⇒σ_i=Av_i/u_i

　　　 这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵Σ。

SVD的一些性质　

　　　　上面几节我们对SVD的定义和计算做了详细的描述，似乎看不出我们费这么大的力气做SVD有什么好处。那么SVD有什么重要的性质值得我们注意呢？

　　　　对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：

                                                   Am×n=Um×mΣm×nV^Tn×n≈Um×kΣk×kV^Tk×n

　　　　其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵Um×k,Σk×k,V^Tk×n来表示。如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。

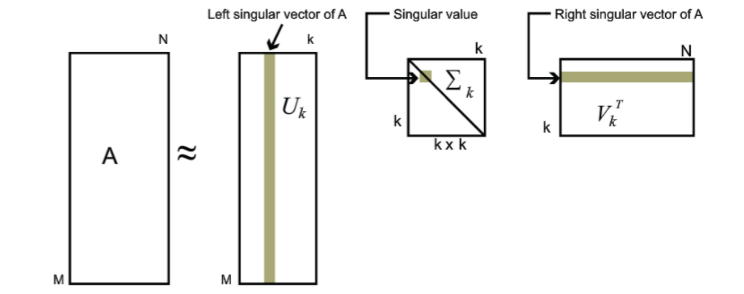
　　　　由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

以上转自：http://www.cnblogs.com/pinard/p/6251584.html

SVD协同过滤：

假设存在以下user和item的数据矩阵：

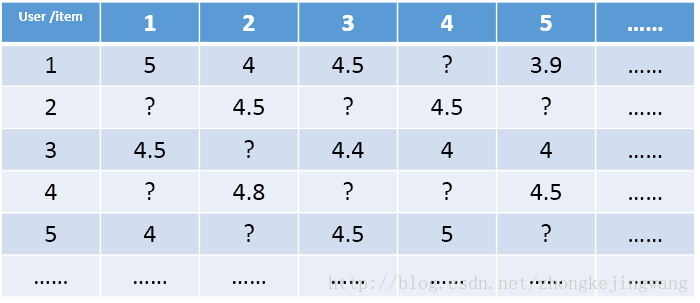
这是一个极其稀疏的矩阵，这里把这个评分矩阵记为R，其中的元素表示user对item的打分，“？”表示未知的，也就是要你去预测的，现在问题来了：如何去预测未知的评分值呢？从上面的SVD的性质:  Am×n=Um×mΣm×nVTn×n≈Um×kΣk×kVTk×n，可以得到：

一个m*n的打分矩阵R可以由分解的两个小矩阵U（m*k）和V（k*n）的乘积来近似，即 R=UV^T,k<=m,n 

将这种分解方式体现协同过滤中，即有：

 (matrix factorization model，MF模型 )

在这样的分解模型中,Pu代表用户隐因子矩阵（表示用户u对因子k的喜好程度),Qi表示电影隐因子矩阵（表示电影i在因子k上的程度）。

SVD推荐算法公式如下：

这里需要解释一下各个参数的含义：

对于电影评分实例，首先得到训练数据集 user_id,movie_id和rating，u表示打分矩阵中所有评分值的平均值，bi在这个公式中应该是一个参数值，而不是向量，可以这样理解，首先初始化一个代表item的向量bi，向量维度是item的个数，公式中的bi是指bi[movie_id],同理，bu代表bu[user_id],r_{ui_}hat 表示预测的评分值.

加入防止过拟合的 λ 参数，可以得到下面的优化函数：

利用随机梯度下降算法更新参数：

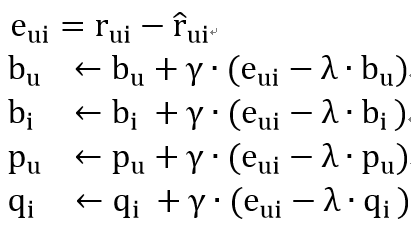
代码体现：

# -*- coding: utf-8 -*-
"""
Created on Thu Apr 19 16:28:10 2018

@author:
"""
import numpy as np
import random
import os 

class SVD:
    def __init__(self,mat,K=20):
        self.mat=np.array(mat)
        self.K=K
        self.bi={}
        self.bu={}
        self.qi={}
        self.pu={}
        self.avg=np.mean(self.mat[:,2])
        for i in range(self.mat.shape[0]):
            uid=self.mat[i,0]
            iid=self.mat[i,1]
            self.bi.setdefault(iid,0)
            self.bu.setdefault(uid,0)
            self.qi.setdefault(iid,np.random.random((self.K,1))/10*np.sqrt(self.K))
            self.pu.setdefault(uid,np.random.random((self.K,1))/10*np.sqrt(self.K))
    def predict(self,uid,iid):  #预测评分的函数
        #setdefault的作用是当该用户或者物品未出现过时，新建它的bi,bu,qi,pu，并设置初始值为0
        self.bi.setdefault(iid,0)
        self.bu.setdefault(uid,0)
        self.qi.setdefault(iid,np.zeros((self.K,1)))
        self.pu.setdefault(uid,np.zeros((self.K,1)))
        rating=self.avg+self.bi[iid]+self.bu[uid]+np.sum(self.qi[iid]*self.pu[uid]) #预测评分公式
        #由于评分范围在1到5，所以当分数大于5或小于1时，返回5,1.
        if rating>5:
            rating=5
        if rating<1:
            rating=1
        return rating  

    def train(self,steps=30,gamma=0.04,Lambda=0.15):    #训练函数，step为迭代次数。
        print('train data size',self.mat.shape)
        for step in range(steps):
            print('step',step+1,'is running')
            KK=np.random.permutation(self.mat.shape[0]) #随机梯度下降算法，kk为对矩阵进行随机洗牌
            rmse=0.0;mae=0
            for i in range(self.mat.shape[0]):
                j=KK[i]
                uid=self.mat[j,0]
                iid=self.mat[j,1]
                rating=self.mat[j,2]
                eui=rating-self.predict(uid, iid)
                rmse+=eui**2
                mae+=abs(eui)
                self.bu[uid]+=gamma*(eui-Lambda*self.bu[uid])
                self.bi[iid]+=gamma*(eui-Lambda*self.bi[iid])
                tmp=self.qi[iid]
                self.qi[iid]+=gamma*(eui*self.pu[uid]-Lambda*self.qi[iid])
                self.pu[uid]+=gamma*(eui*tmp-Lambda*self.pu[uid])
            gamma=0.93*gamma  #gamma以0.93的学习率递减
            print('rmse is {0:3f}, ase is {1:3f}'.format(np.sqrt(rmse/self.mat.shape[0]),mae/self.mat.shape[0]))  

    def test(self,test_data):   

        test_data=np.array(test_data)
        print('test data size',test_data.shape)
        rmse=0.0;mae=0
        for i in range(test_data.shape[0]):
            uid=test_data[i,0]
            iid=test_data[i,1]
            rating=test_data[i,2]
            eui=rating-self.predict(uid, iid)
            rmse+=eui**2
            mae+=abs(eui)
        print('rmse is {0:3f}, ase is {1:3f}'.format(np.sqrt(rmse/self.mat.shape[0]),mae/self.mat.shape[0]))  

def getData(file_name):
    """
    获取训练集和测试集的函数
    """
    data=[]
    with open(os.path.expanduser(file_name)) as f:
        for line in f.readlines():
            list=line.split('::')
            data.append([int(i) for i in list[:3]])
    random.shuffle(data)
    train_data=data[:int(len(data)*7/10)]
    test_data=data[int(len(data)*7/10):]
    print('load data finished')
    print('total data ',len(data))
    return train_data,test_data  

if __name__=='__main__':
    train_data,test_data=getData('D:/Downloads/ml-1m/ratings.dat')
    a=SVD(train_data,30)
    a.train()
    a.test(test_data)  

测试结果

在训练集上
rmse is 0.869038, ase is 0.690794
在测试集上
rmse is 0.583027, ase is 0.303116

 SVD++算法：

SVD算法是指在SVD的基础上引入隐式反馈，使用用户的历史浏览数据、用户历史评分数据等作为新的参数。

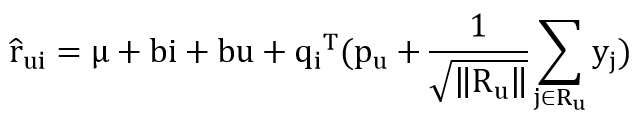
这里的N(u)表示用户u行为记录（包括浏览的和评过分的商品集合），yj为隐藏的“评价了电影 j”反映出的个人喜好偏置。其他参数同SVD中的参数含义一致。

利用随机梯度下降算法更新参数：

代码体现：

# -*- coding: utf-8 -*-
"""
Created on Sat Apr 21 14:44:25 2018

@author: fanchao3
"""
import numpy as np
import random
import os

class SVDPP:
    def __init__(self,mat,K=20):
        self.mat=np.array(mat)
        self.K=K
        self.bi={}
        self.bu={}
        self.qi={}
        self.pu={}
        self.avg=np.mean(self.mat[:,2])
        self.y={}
        self.u_dict={}
        for i in range(self.mat.shape[0]):  

            uid=self.mat[i,0]
            iid=self.mat[i,1]
            self.u_dict.setdefault(uid,[])
            self.u_dict[uid].append(iid)
            self.bi.setdefault(iid,0)
            self.bu.setdefault(uid,0)
            self.qi.setdefault(iid,np.random.random((self.K,1))/10*np.sqrt(self.K))
            self.pu.setdefault(uid,np.random.random((self.K,1))/10*np.sqrt(self.K))
            self.y.setdefault(iid,np.zeros((self.K,1))+.1)
    def predict(self,uid,iid):  #预测评分的函数
        #setdefault的作用是当该用户或者物品未出现过时，新建它的bi,bu,qi,pu及用户评价过的物品u_dict，并设置初始值为0
        self.bi.setdefault(iid,0)
        self.bu.setdefault(uid,0)
        self.qi.setdefault(iid,np.zeros((self.K,1)))
        self.pu.setdefault(uid,np.zeros((self.K,1)))
        self.y.setdefault(uid,np.zeros((self.K,1)))
        self.u_dict.setdefault(uid,[])
        u_impl_prf,sqrt_Nu=self.getY(uid, iid)
        rating=self.avg+self.bi[iid]+self.bu[uid]+np.sum(self.qi[iid]*(self.pu[uid]+u_impl_prf)) #预测评分公式
        #由于评分范围在1到5，所以当分数大于5或小于1时，返回5,1.
        if rating>5:
            rating=5
        if rating<1:
            rating=1
        return rating  

    #计算sqrt_Nu和∑yj
    def getY(self,uid,iid):
        Nu=self.u_dict[uid]
        I_Nu=len(Nu)
        sqrt_Nu=np.sqrt(I_Nu)
        y_u=np.zeros((self.K,1))
        if I_Nu==0:
            u_impl_prf=y_u
        else:
            for i in Nu:
                y_u+=self.y[i]
            u_impl_prf = y_u / sqrt_Nu  

        return u_impl_prf,sqrt_Nu  

    def train(self,steps=30,gamma=0.04,Lambda=0.15):    #训练函数，step为迭代次数。
        print('train data size',self.mat.shape)
        for step in range(steps):
            print('step',step+1,'is running')
            KK=np.random.permutation(self.mat.shape[0]) #随机梯度下降算法，kk为对矩阵进行随机洗牌
            rmse=0.0
            for i in range(self.mat.shape[0]):
                j=KK[i]
                uid=self.mat[j,0]
                iid=self.mat[j,1]
                rating=self.mat[j,2]
                predict=self.predict(uid, iid)
                u_impl_prf,sqrt_Nu=self.getY(uid, iid)
                eui=rating-predict
                rmse+=eui**2
                self.bu[uid]+=gamma*(eui-Lambda*self.bu[uid])
                self.bi[iid]+=gamma*(eui-Lambda*self.bi[iid])
                self.pu[uid]+=gamma*(eui*self.qi[iid]-Lambda*self.pu[uid])
                self.qi[iid]+=gamma*(eui*(self.pu[uid]+u_impl_prf)-Lambda*self.qi[iid])
                for j in self.u_dict[uid]:
                    self.y[j]+=gamma*(eui*self.qi[j]/sqrt_Nu-Lambda*self.y[j])  

            gamma=0.93*gamma
            print('rmse is',np.sqrt(rmse/self.mat.shape[0]))  

    def test(self,test_data):  #gamma以0.93的学习率递减  

        test_data=np.array(test_data)
        print('test data size',test_data.shape)
        rmse=0.0
        for i in range(test_data.shape[0]):
            uid=test_data[i,0]
            iid=test_data[i,1]
            rating=test_data[i,2]
            eui=rating-self.predict(uid, iid)
            rmse+=eui**2
        print('rmse of test data is',np.sqrt(rmse/test_data.shape[0]))  

def getData(file_name):
    """
    获取训练集和测试集的函数
    """
    data=[]
    with open(os.path.expanduser(file_name)) as f:
        for line in f.readlines():
            list=line.split('::')
            data.append([int(i) for i in list[:3]])
    random.shuffle(data)
    train_data=data[:int(len(data)*7/10)]
    test_data=data[int(len(data)*7/10):]
    print('load data finished')
    print('total data ',len(data))
    return train_data,test_data  

if __name__=='__main__':
    train_data,test_data=getData('D:/Downloads/ml-1m/ratings.dat')
    a=SVDPP(train_data,30)
    a.train()
    a.test(test_data)  

# -*- coding: utf-8 -*-
"""
Created on Thu Apr 19 17:53:34 2018

@author:
"""

import numpy as np
import random
import os 

class SVDPP:
    def __init__(self,mat,K=20):
        self.mat=np.array(mat)
        self.K=K
        self.avg=np.mean(self.mat[:,2])
        self.user_num = len(set(self.mat[:,0]))
        self.item_num = len(set(self.mat[:,1]))
        #print("item_num:",self.item_num )
        #user bias
        self.bu = np.zeros(self.user_num, np.double)

        #item bias
        self.bi = np.zeros(self.item_num, np.double)

        #user factor
        self.p = np.zeros((self.user_num, self.K), np.double) + .1

        #item factor
        self.q = np.zeros((self.item_num, self.K), np.double) + .1

        #item preference facotor
        self.y = np.zeros((self.item_num, self.K), np.double) + .1
        self.u_items={}
        for i in range(self.mat.shape[0]):
            uid=self.mat[i,0]
            iid=self.mat[i,1]
            if uid not in self.u_items.keys():
                self.u_items[uid]=[iid]
            else:
                self.u_items[uid].append(iid)

    def train(self,steps=30,gamma=0.04,Lambda=0.15):    #训练函数，step为迭代次数。
        #print('train data size',self.mat.shape) 

        for step in range(steps):
            print('step',step+1,'is running')
            KK=np.random.permutation(self.mat.shape[0]) #随机梯度下降算法，kk为对矩阵进行随机洗牌
            rmse=0.0;mae=0
            for i in range(self.mat.shape[0]):
                j=KK[i]
                uid=self.mat[j,0]
                iid=self.mat[j,1]
                rating=self.mat[j,2]
                Nu=self.u_items[uid]
                I_Nu = len(Nu)
                sqrt_N_u = np.sqrt(I_Nu)
                #基于用户u点评的item集推测u的implicit偏好
                y_u = np.sum(self.y[Nu], axis=0)
                u_impl_prf = y_u / sqrt_N_u
                #预测值
                rp = self.avg + self.bu[uid] + self.bi[iid] + np.dot(self.q[iid], self.p[uid] + u_impl_prf)
                eui=rating- rp
                rmse+=eui**2
                mae+=abs(eui)
                #sgd
                self.bu[uid] += gamma * (eui - Lambda * self.bu[uid])
                self.bi[iid] += gamma * (eui - Lambda * self.bi[iid])
                self.p[uid] += gamma * (eui * self.q[iid] - Lambda * self.p[uid])
                self.q[iid] += gamma * (eui * (self.p[uid] + u_impl_prf) - Lambda * self.q[iid])
                for j in Nu:
                    self.y[j] += gamma * (eui * self.q[j] / sqrt_N_u - Lambda * self.y[j])

            gamma=0.93*gamma  #gamma以0.93的学习率递减
            print('rmse is {0:3f}, ase is {1:3f}'.format(np.sqrt(rmse/self.mat.shape[0]),mae/self.mat.shape[0]))  

    def test(self,test_data):   

        test_data=np.array(test_data)
        print('test data size',test_data.shape)
        rmse=0.0;mae=0
        for i in range(test_data.shape[0]):
            uid=test_data[i,0]
            iid=test_data[i,1]
            Nu=self.u_items[uid]
            I_Nu = len(Nu)
            sqrt_N_u = np.sqrt(I_Nu)
            y_u = np.sum(self.y[Nu], axis=0) / sqrt_N_u
            est = self.avg + self.bu[uid] + self.bi[iid] + np.dot(self.q[iid], self.p[uid] + y_u)
            rating=test_data[i,2]
            eui=rating-est
            rmse+=eui**2
            mae+=abs(eui)
        print('rmse is {0:3f}, ase is {1:3f}'.format(np.sqrt(rmse/self.mat.shape[0]),mae/self.mat.shape[0]))  

def getData(file_name):
    """
    获取训练集和测试集的函数
    """
    data=[]
    with open(os.path.expanduser(file_name)) as f:
        for line in f.readlines():
            List=line.split('::')
            data.append([int(i) for i in List[:3]])  

    random.shuffle(data)
    train_data=data[:int(len(data)*7/10)]
    test_data=data[int(len(data)*7/10):]
    new_train_data=mapping(train_data)
    new_test_data=mapping(test_data)
    print('load data finished')
    return new_train_data,new_test_data
def mapping(data):
    """
    将原始的uid，iid映射为从0开始的编号
    """
    data=np.array(data)
    users=list(set(data[:,0]))
    u_dict={}
    for i in range(len(users)):
        u_dict[users[i]]=i
    items=list(set(data[:,1]))
    i_dict={}
    for j in range(len(items)):
        i_dict[items[j]]=j
    new_data=[]
    for l in data:
        uid=u_dict[l[0]]
        iid=i_dict[l[1]]
        r=l[2]
        new_data.append([uid,iid,r])
    return new_data

if __name__=='__main__':
    train_data,test_data=getData('D:/Downloads/ml-1m/ratings.dat')
    a=SVDPP(train_data,30)
    a.train()
    a.test(test_data)