Codeforces 461D. Appleman and Complicated Task 构造,计数

原文链接https://www.cnblogs.com/zhouzhendong/p/CF461D.html

题解

首先我们可以发现如果确定了第一行，那么方案就唯一了。

然后，我们来看看一个点的值确定了会导致什么：

假设我们确定了红色点的值，那么所有包含橙色的格子xor起来就等于红色格子的值，绿色蓝色也是。

第一排就比较特殊了。

如果我们在对第一排奇偶分类之后，如果我们可以得到第一行的前缀xor之间的关系，那么我们就有希望解决这个问题。

再看一种情况：

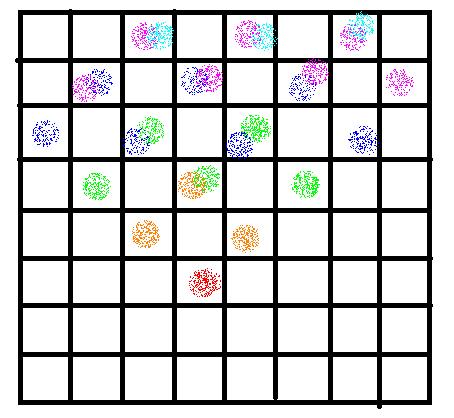
类似地意思，我们会发现这个东西遇到墙会反射。

于是我们就基本可以通过权值并查集来搞定。

我们还剩下一个问题：

这样的方式还不能确定最下面一行是否满足条件。

我们来看一个东西：

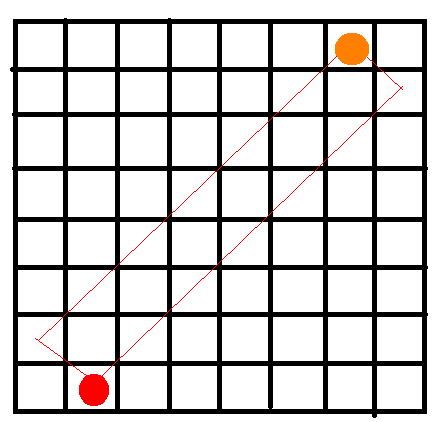
通过这个我们可以意识到，第一行和最后一行是一一对应的。于是整个局面旋转180度还是一样的。于是只要第一行合法，那么最后一行也合法。

所以我们只要通过给出的点用权值并查集维护一下第一行，然后算一下答案就好了。

代码

#pragma GCC optimize(2)
#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
#define For(i,a,b) for (int i=a;i<=b;i++)
#define Fod(i,b,a) for (int i=b;i>=a;i--)
using namespace std;
typedef long long LL;
LL read(){
	LL x=0,f=0;
	char ch=getchar();
	while (!isdigit(ch))
		f|=ch=='-',ch=getchar();
	while (isdigit(ch))
		x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
	return f?-x:x;
}
const int N=100005,mod=1e9+7;
int n,k;
int fa[N],d[N];
int getf(int x){
	if (fa[x]==x)
		return x;
	int f=getf(fa[x]);
	d[x]^=d[fa[x]];
	return fa[x]=f;
}
int Pow(int x,int y){
	int ans=1;
	for (;y;y>>=1,x=(LL)x*x%mod)
		if (y&1)
			ans=(LL)ans*x%mod;
	return ans;
}
int main(){
	n=read(),k=read();
	For(i,0,n)
		fa[i]=i;
	while (k--){
		int x=read(),y=read(),z;
		char s[10];
		scanf("%s",s);
		z=s[0]=='x'?0:1;
		int L=y-(x-1);
		if (L<1)
			L=1+(1-L);
		int R=y+(x-1);
		if (R>n)
			R=n-(R-n);
		L=max(0,L-2);
		if (getf(L)!=getf(R))
			d[fa[L]]=z^d[L]^d[R],fa[fa[L]]=fa[R];
		else if (d[L]^d[R]^z)
			return puts("0"),0;
	}
	int ans=-1;
	For(i,0,n)
		if (fa[i]==i)
			ans++;
	if (ans==-1)
		assert(0);
	cout<<Pow(2,ans)<<endl;
	return 0;
}