python田忌赛马

一，简介

田忌赛马的故事大家都知道我就不展开说了，田忌能用同全面被碾压的马赢了齐威王（公子），我觉得这是十分具有智慧的。但是，如果说这里的条件改为：1，田忌的马比齐威王同等次的马弱一点但是比齐威王下一等次的马强一点。2，无法从对方马的外观看出马的等次。3，用完的马不能再用。问田忌赢了齐威王的概率是多少？

二，实验设计

1，首先，三局两胜制，我们这里把田忌3局里赢的场数算出来。

　　我们初始化马用list中值的大小来比较马的能力，可见田忌的马相对于公子的马来说辣鸡不少。

　　t = [2, 5, 8]  #田忌的马
　　g = [3, 6, 9]  #公子的马

　　 用完的马不能再次上场（马也要休息啊），那么每次比完的马就从list中remove掉，得出：

 # 田忌公子博弈策略
 def tianji_gongzi():  #田忌千场胜利次数
     winer_perchang = []    #每场的胜者
     t = [2, 5, 8]
     g = [3, 6, 9]
     N = 2
     for i in range(0,3):
         para1 = random.randint(0,N)  #这里设置N是因为list变短了，randint随机范围变小了
         para2 = random.randint(0,N)
         N = N -1
         #print(t[para1],g[para2])
         if t[para1] > g[para2]:
             #print("田忌胜")
             winer_perchang.append(1)
         else:
             #print("公子胜")
             pass
         t.remove(t[para1])
         g.remove(g[para2])

     return len(winer_perchang)

这里主要讲的是俩人的对战策略，都是随机从自己的马棚找马出来应战，最终返回的值是3局里田忌赢的场数（winer_perchang），注意这里的“N=2”是因为remove之后就没两个了，所以用“

N = N -1”来设置一下。

2，田忌每1000次能赢多少次？

这里的参数“times”我设置的是1000，就是说比了1000场（不考虑马累死哈），每场比3局，调用“tianji_gongzi()”函数把每场田忌赢的局数返回回来，当田忌每场赢了2局或者以上证明忌哥这场赢了，就加入到list“

win_timesfor_t”中，这里用“len(win_timesfor_t)”表示这1000场里田忌赢得场次，并返回这个数。

 def t_win_persouthand(times):
     win_timesfor_t = []   #田忌赢的次数的记录
     for i in range(0,times):
         a = tianji_gongzi()
         if a >= 2:
         #print("返回值", a)  # 田忌每场胜利的次数
             win_timesfor_t.append(a)
     #print("每times次田忌赢的次数为：",len(win_timesfor_t))
     return len(win_timesfor_t)

3，每1000场田忌赢得场数算出来了，接下来就算100个1000场的数据（马是真的累）

调用函数“t_win_persouthand(times)”得到1000场胜利场数，再循环100次让他们再比100个1000场，得到100个千场胜率，最后将数据画出来。

 if __name__ == '__main__':
     y_pait = []
     n = 100   #实验次数
     y_pait = paint(n)
     #print(y_pait)
     x_pait = []
     for i in range(1,n+1):
         x_pait.append(i)
     #print(x_pait)

     sum = 0
     for i in y_pait:
         sum = sum + i
     average = sum/n
     print('田忌每 ',n,' 次模拟的千场胜率为：',average/10,"%")

     plt.plot(x_pait,y_pait, label='NM')
     # plt.plot(x2, y2, label='Second Line')
     plt.xlabel('Iterations')  # 横坐标标题
     plt.ylabel('Win_times per 1000 iterations')  # 纵坐标标题
     # plt.title('Interesting Graph\nCheck it out',loc="right")   #图像标题
     plt.title('Paragraph for hourse strategy')
     plt.legend()  # 显示Fisrt Line和Second Line（label）的设置
     plt.savefig('C:/Users/zhengyong/Desktop/1.png')
     plt.show()

　　这里又调用了“t_win_persouthand(times)”中return的“return len(win_timesfor_t)”，然后加入list并画图。

　　最后我们计算出了100个千场平均胜率，说白了就是比了100000场，让马跑这么多次也主要是为了结果精确。

　　注意，这里是好几次嵌套调用，要注意哈。

全部代码：

 import random
 import matplotlib.pyplot as plt

 # 田忌公子博弈策略
 def tianji_gongzi():  #田忌千场胜利次数
     winer_perchang = []    #每场的胜者
     t = [2, 5, 8]
     g = [3, 6, 9]
     N = 2
     for i in range(0,3):
         para1 = random.randint(0,N)  #这里设置N是因为list变短了，randint随机范围变小了
         para2 = random.randint(0,N)
         N = N -1
         #print(t[para1],g[para2])
         if t[para1] > g[para2]:
             #print("田忌胜")
             winer_perchang.append(1)
         else:
             #print("公子胜")
             pass
         t.remove(t[para1])
         g.remove(g[para2])

     return len(winer_perchang)

 def t_win_persouthand(times):
     win_timesfor_t = []   #田忌赢的次数的记录
     for i in range(0,times):
         a = tianji_gongzi()
         if a >= 2:
         #print("返回值", a)  # 田忌每场胜利的次数
             win_timesfor_t.append(a)
     #print("每times次田忌赢的次数为：",len(win_timesfor_t))
     return len(win_timesfor_t)

 #t_win_persouthand(1000)
 def paint(N):
     win_times = []
     for i in range(0,N):   #这里要100个数据
         b = t_win_persouthand(1000)
         win_times.append(b)
     #print(win_times)  #list中装的是没times（这里是1000）次田忌赢的次数
     return win_times

 if __name__ == '__main__':
     y_pait = []
     n = 100   #实验次数
     y_pait = paint(n)
     #print(y_pait)
     x_pait = []
     for i in range(1,n+1):
         x_pait.append(i)
     #print(x_pait)

     sum = 0
     for i in y_pait:
         sum = sum + i
     average = sum/n
     print('田忌每 ',n,' 次模拟的千场胜率为：',average/10,"%")

     plt.plot(x_pait,y_pait, label='NM')
     # plt.plot(x2, y2, label='Second Line')
     plt.xlabel('Iterations')  # 横坐标标题
     plt.ylabel('Win_times per 1000 iterations')  # 纵坐标标题
     # plt.title('Interesting Graph\nCheck it out',loc="right")   #图像标题
     plt.title('Paragraph for hourse strategy')
     plt.legend()  # 显示Fisrt Line和Second Line（label）的设置
     plt.savefig('C:/Users/zhengyong/Desktop/1.png')
     plt.show()

三，结果

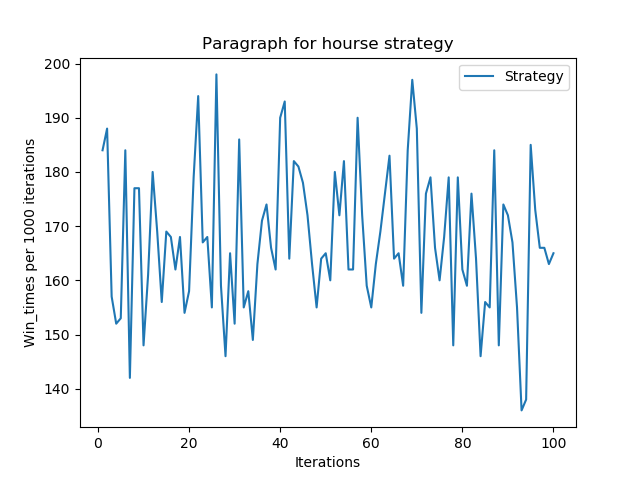
以上是模拟出来的结果图示，下面是概率。

四，总结

　　总体来说，代码很简单，就是练练手，几个变量的全局性考虑下，循环时候remove注意下就好了。

　　算了几次，基本上是15.5-15.8之间吧，折痕容易联想到六分之一，具体是不是我们以后验证哈。

　　

　　增订一下数学解法：

第三种方法：穷举法，这个其实也不多，读者自己可以试试看。

数学方法只是验证一下我们通过随机数的分布概率得到的结果，大家可以通过修改参数看看小样本下是怎样的情况。