[NOIP2016] 天天爱跑步 桶 + DFS

～～～题面～～～

题解：

很久以前就想写了，一直没敢做，，，不过今天写完没怎么调就过了还是很开心的。

首先我们观察到跑步的人数是很多的，要一条一条的遍历显然是无法承受的，因此我们要考虑更加优美的方法。

首先我们假设观察者没有时间的限制，一天到晚都在观察。那么我们可以想到一个很显然的做法——差分。这样就可以很方便的求出一个点被经过了多少次。

貌似这样再加想一下就可以直接用树链剖分+差分搞了。

但是还有更好的算法，是O(n)的。

而且还是比较好写的。

首先我们观察可以被统计到的点要符合一个什么条件。

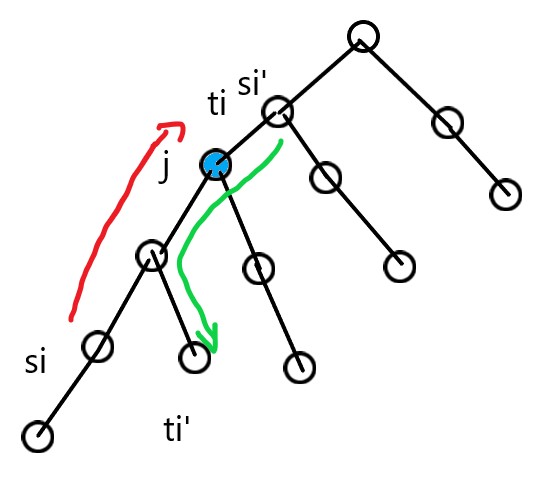
设点j上的观察者在w[j]的时候观察，那么也就是说从s出发，要刚好经过w[j]到达点j，才可以被点j上的观察者统计到。

由此我们可以列出两个式子：

1，当s在j的子树内，而t在j的上方时。

　　$w[j] + dep[j] = dep[s_i]$

2，当t在j的子树内，而s在j的上方时

　　$dis[i] - (dep[t_i] - dep[j]) = w[j]$ 其中dis[i]表示s ---> t的路程长度

　　因为dis[i] - (dep[t_i] - dep[j])其实就是s ---> j的路径长，所以这个式子就显然成立了。

　　如果我们将带i的放在左边，带j的放在右边，那么将会有

　　$dis[i] - dep[t_i] = w[j] - dep[j]$

那s和t都在j的子树内怎么办？（都在上方显然不会统计到）

　　现在这时如果我们还是套用上面的式子，那么会有两种情况

　　(1),j是(s,t)的LCA，那么此时两个式子一旦其中之一被满足，另外一个就一定会被满足（因为两个式子的实质是一样的），那么s和t将分别对j产生一次贡献（否则没有贡献）

　　(2),j不是(s,t)的LCA，那么此时两个式子可能会被满足，s和t不一定会对j产生贡献。但是这种情况下，不论式子是否被满足，s和t都是不应该对j产生贡献的。
　　那么我们怎么避免这种情况？

　　　　首先我们注意到一旦这种情况出现，LCA[s,t]将会是s和t最后一次可能产生贡献的地方，因此我们要在LCA[s,t]处，消除s和t的影响，使得s和t无法对上面的点产生贡献。

那么我们应该如何统计呢？

　　注意到所有的式子都可以被表示为左边只有关于i的，右边只有关于j的情况，因此我们完全可以将式子的左边和右边单独计算。即分别用两个桶统计关于两个式子的满足情况。

比如说我们定义int bu[600100];  然后每次遇到一个$s_i$的时候，我们就令$dep[s_i]++$。然后我们在每进入一个点时，都记录一个tmp = bu[w[j] + dep[j]]，那么桶内对应位置元素的个数就代表满足

$dep[s_i] = t$（t为桶中位置）的元素个数。因此我们访问bu[w[j] + dep[j]]就可以获取满足 $w[j] + dep[j] = dep[s_i]$ 的元素个数，而之所以要在进入之前先记录一下位置，则是为了准确获取子树内的贡献，保证不被之前的东西干扰。

　　对第二个式子的处理方式也是类似的，只不过因为第二个式子中出现了减号，而且减号旁边大小关系不确定，因此我们需要的桶中位置可能为负，所以我们统一加上一个较大的数，将本来要占据负数的数组整体向后移位就可以了。

具体实现看代码。

 #include<bits/stdc++.h>
 using namespace std;
 #define R register int
 #define AC 501000
 #define ac 910000//要开这么大。。。
 #define getchar() *o++
 char READ[], *o = READ;
 int n, m;
 int w[AC], ans[AC], s[AC], t[AC], dis[AC], dep[AC], may[ac], id[ac];
 int Head[AC], Next[ac], date[ac], tot;
 struct edge{
     int Head[AC], Next[ac], date[ac], tot;
     inline void add(int f, int w)
     {
         date[++tot] = w, Next[tot] = Head[f], Head[f] = tot;
         date[++tot] = f, Next[tot] = Head[w], Head[w] = tot;
     }
 }E1,E2,E3;//询问的边(LCA)，查询的边(ans) 
 
 inline int read()
 {
     int x = ; char c = getchar();
     while(c > '' || c < '') c = getchar();
     while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
     return x;
 }
 
 inline void add(int f, int w)
 {
     date[++tot] = w, Next[tot] = Head[f], Head[f] = tot;
     date[++tot] = f, Next[tot] = Head[w], Head[w] = tot;
 }
 
 inline void add1(int f, int w, int S)
 {
     E3.date[++tot] = w, E3.Next[tot] = E3.Head[f], E3.Head[f] = tot, may[tot] = S;
 }
 
 inline void add2(int f, int w)//这里只能连单向边
 {
     E2.date[++tot] = w, E2.Next[tot] = E2.Head[f], E2.Head[f] = tot;
 }
 
 void pre()
 {
     int a, b;
     n = read(), m = read();
     for(R i = ; i < n; i++)
     {
         a = read(), b = read();
         add(a, b);
     }
     for(R i = ; i <= n; i++) w[i] = read();
     E1.tot = E2.tot = tot = ;
     for(R i = ; i <= m; i++)
     {
         s[i] = read(), t[i] = read();
         E1.add(s[i], t[i]);
         add1(s[i], i, );//标记为开始节点
         add1(t[i], i, );//标记为结束节点
         id[E1.tot - ] = id[E1.tot] = i;
     }
 }
 
 struct get_LCA{
     int father[AC], LCA[ac]; bool z[AC];
 
     inline int find(int x)
     {
          return (x == father[x]) ? x : father[x] = find(father[x]);
     }
 
     void dfs(int x)
     {
         int now;
         z[x] = true;
         for(R i = Head[x]; i; i = Next[i])
         {
             now = date[i];
             if(z[now]) continue;
             dep[now] = dep[x] + ;
             dfs(now);
             father[now] = x;//访问完就要改父亲了
         }
         for(R i = E1.Head[x]; i; i = E1.Next[i])
         {
             now = E1.date[i];
             if(z[now] && !LCA[i ^ ])
             {
             //    printf("%d %d\n", x, now);
                 LCA[i] = find(now);
                 dis[id[i]] = dep[x] - dep[LCA[i]] + dep[now] - dep[LCA[i]];
                 add2(LCA[i], id[i]);//将LCA和询问联系起来
             }
         }
     }
 
     void getLCA()
     {
         for(R i = ; i <= n; i++) father[i] = i;
         dep[] = ;
         dfs();
     }
 }LCA;
 
 #define k 600000
 struct difference{
     int bu[ac], b[ac * ];
     void dfs(int x, int fa)
     {
         int tmp = bu[dep[x] + w[x]], rnt = b[w[x] - dep[x] + k], now;
         for(R i = E3.Head[x]; i; i = E3.Next[i])//加上当前节点的贡献
         {
             now = E3.date[i];
             if(!may[i]) ++bu[dep[x]];//如果是开始节点
             else ++b[dis[now] - dep[x] + k];//等式两边同时+k
         }
         for(R i = Head[x]; i; i = Next[i])//遍历子树
         {
             now = date[i];
             if(now == fa) continue;
             dfs(now, x);
         }
         ans[x] = bu[dep[x] + w[x]] - tmp + b[w[x] - dep[x] + k] - rnt;
         for(R i = E2.Head[x]; i; i = E2.Next[i])//查看当前节点是哪些点对的LCA
         {
             now = E2.date[i];
             if(dep[s[now]] == dep[x] + w[x]) --ans[x];//如果造成了贡献，那么必定是双倍，因此要减去
             --bu[dep[s[now]]];//减去贡献
             --b[dis[now] - dep[t[now]] + k];//等式两边同时+k!
         }
     }
 
 }get;
 
 void work()
 {
     for(R i = ; i <= n; i++) printf("%d ", ans[i]);
     printf("\n");
 }
 
 int main()
 {
     freopen("in.in", "r", stdin);
     fread(READ, , , stdin);
     pre();
     LCA.getLCA();
     get.dfs(, );
     work();
     fclose(stdin);
     return ;
 }