Leetcode 之 Combination Sum系列

39. Combination Sum

1.Problem

Find all possible combinations of k numbers that add up to a number n, given that only numbers from 1 to 9 can be used and each combination should be a unique set of numbers.

Example 1:

Input: k = 3, n = 7

Output:

[[1,2,4]]

Example 2:

Input: k = 3, n = 9

Output:

[[1,2,6], [1,3,5], [2,3,4]]

2.Solution

题目的大意是给定一个元素不存在重复的一维数组candidates和一个目标数target，输出由一位数组中的数可以组成target的所有组合类型，注：candidates中的数可以重复使用的。

对给定的数组进行排序，然后针对target进行回溯。

3.Code

 package test;

 import java.util.ArrayList;

 import java.util.Arrays;

 import java.util.List;

 public class TaskTest {

     private List<List<Integer>> result = new ArrayList<List<Integer>>();

     private int[] temp;

     public static void main(String[] args) {

         int[] a = {2,3,6,7};

         new TaskTest().combinationSum(a,7);

         //System.out.println();

     }

     public List<List<Integer>> combinationSum(int[] candidates, int target) {

         //[2, 3, 6, 7] and target 7

         this.temp = candidates;

         Arrays.sort(temp);

         List<Integer> current = new ArrayList<>();

         backTracing(current,0,target);

         System.out.println(this.result.toString());

         return result;

     }

     public void backTracing(List<Integer> current , int index , int target) {

         if ( target == 0 ) {

             List<Integer> list = new ArrayList<>(current);

             result.add(list);

         } else {

             for ( int i = index ; i < temp.length && temp[i] <= target ; i++ ) {

                 current.add(temp[i]);

                 backTracing(current,i,target - temp[i]);

                 current.remove(new Integer(temp[i]));

             }

         }

     }

 }

4.提交Leetcode的代码

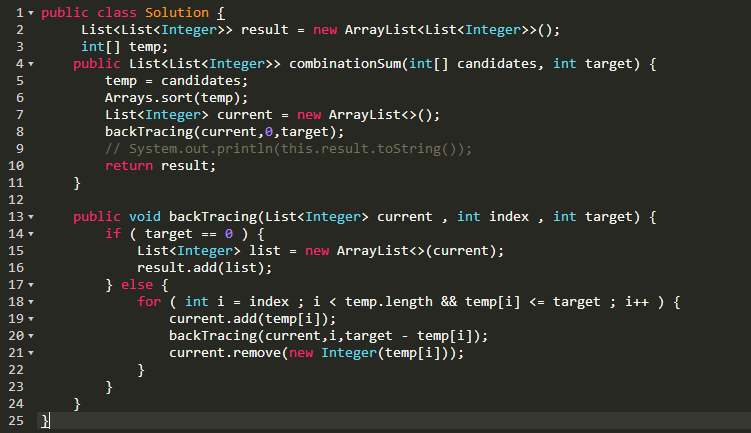
40. Combination Sum II

1.Problem

Given a collection of candidate numbers (C) and a target number (T), find all unique combinations in C where the candidate numbers sums to T.

Each number in C may only be used once in the combination.

Note:

All numbers (including target) will be positive integers.
The solution set must not contain duplicate combinations.

For example, given candidate set [10, 1, 2, 7, 6, 1, 5] and target 8,
A solution set is:

[

  [1, 7],

  [1, 2, 5],

  [2, 6],

  [1, 1, 6]

]

2.Soluton

Combination Sum II跟 I比不同点在于，II中的一维数组中元素允许重复，但是组成target的每个元素仅允许被使用一次

backTracing(current,i + 1 ,target - temp[i]); 位置变为 i + 1
处理结果中存在的重复问题
输出的结果跟顺序无关，即([[1,1,6],[1,2,5],[1,7],[2,6]]) 和([[1,2,5],[1,1,6],[2,6],[1,7]])是相同的，都是正确的结果

3.Code

 package test;

 import java.util.ArrayList;

 import java.util.Arrays;

 import java.util.HashSet;

 import java.util.Iterator;

 import java.util.List;

 import java.util.Set;

 public class TaskTest {

     private List<List<Integer>> result = new ArrayList<List<Integer>>();

     private int[] temp;

     public static void main(String[] args) {

         int[] a = {1,1,2,5,6,7,10};

         new TaskTest().combinationSum(a,8);

         //System.out.println();

     }

     public List<List<Integer>> combinationSum(int[] candidates, int target) {

         //[2, 3, 6, 7] and target 7

         this.temp = candidates;

         Arrays.sort(temp);

         List<Integer> current = new ArrayList<>();

         backTracing(current,0,target);

         System.out.println(this.result.toString());

         Set<List<Integer>> set = new HashSet<>();

         for (List<Integer> l : result ) {

             if ( !set.contains(l)) {

                 set.add(l);

             }

         }

         System.out.println(set.toString());

         result.clear();

         Iterator<List<Integer>> i = set.iterator();

         while ( i.hasNext() ) {

           result.add(i.next());

         }

         System.out.println(result.toString());

         return result;

     }

     public void backTracing(List<Integer> current , int index , int target) {

         if ( target == 0 ) {

             List<Integer> list = new ArrayList<>(current);

             result.add(list);

         } else {

             for ( int i = index ; i < temp.length && temp[i] <= target ; i++ ) {

                 current.add(temp[i]);

                 backTracing(current,i + 1 ,target - temp[i]);

                 current.remove(new Integer(temp[i]));

             }

         }

     }

 }

4.提交Leetcode的代码

216. Combination Sum III

1.Problem

Find all possible combinations of k numbers that add up to a number n, given that only numbers from 1 to 9 can be used and each combination should be a unique set of numbers.

Example 1:

Input: k = 3, n = 7

Output:

[[1,2,4]]

Example 2:

Input: k = 3, n = 9

Output:

[[1,2,6], [1,3,5], [2,3,4]]

2.Solution

一维数组固定为{1,2,3,4,5,6,7,8,9}，要求了组成target的数的个数，同样要求数字不能重复使用

3.Code

package test;

import java.util.ArrayList;

import java.util.Arrays;

import java.util.HashSet;

import java.util.Iterator;

import java.util.List;

import java.util.Set;

public class TaskTest {

    private List<List<Integer>> result = new ArrayList<List<Integer>>();

    private int[] temp = {1,2,3,4,5,6,7,8,9};

    public static void main(String[] args) {

        new TaskTest().combinationSum(3,9);

        //System.out.println();

    }

    public List<List<Integer>> combinationSum(int k, int target) {

        //[2, 3, 6, 7] and target 7

        List<Integer> current = new ArrayList<>();

        backTracing(current,0,target);

        for ( int i = 0 ; i < result.size() ; i++ ) {

            List<Integer> l = result.get(i);

            if (l.size() != k ) {

                System.out.println(l.toString());

                result.remove(i);

                i--;

            }

        }

        System.out.println(result.toString());

        return result;

    }

    public void backTracing(List<Integer> current , int index , int target) {

        if ( target == 0 ) {

            List<Integer> list = new ArrayList<>(current);

            result.add(list);

        } else {

            for ( int i = index ; i < temp.length && temp[i] <= target ; i++ ) {

                current.add(temp[i]);

                backTracing(current,i + 1 ,target - temp[i]);

                current.remove(new Integer(temp[i]));

            }

        }

    }

}

4.提交Leetcode的代码

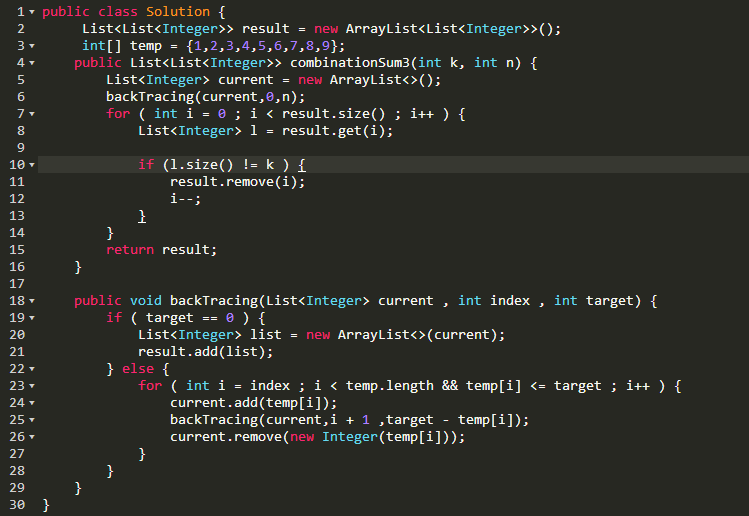
377. Combination Sum IV

1.Problem

Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target.

Example:

nums = [1, 2, 3]

target = 4

The possible combination ways are:

(1, 1, 1, 1)

(1, 1, 2)

(1, 2, 1)

(1, 3)

(2, 1, 1)

(2, 2)

(3, 1)

Note that different sequences are counted as different combinations.

Therefore the output is 7.

2.Solution

动态规划，转移方程为:dp[n] = dp[n] + dp[n-nums[k]] (dp[0] = 1, 即n - nums[k] == 0时 )，dp[i] 代表给定的数组能组成i的种类数

3.Code

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        Arrays.sort(nums);
        DP(target , nums , dp);
        return dp[target];
    }

    public void DP ( int target , int[] nums , int[] dp ) {
       for ( int i = 1 ; i <= target ; i++ ) {
            for ( int j = 0 ; j < nums.length ; j++ ) {
                if ( i - nums[j] >= 0 ) {
                    dp[i] = dp[i] + dp[ i - nums[j] ];
                } else {
                    break;
                }
            }
       }
    }
}

//预先对nums进行排序然后循环中加break，leetcode 提交从18.02%提升到65.16%

4.提交Leetcode的代码