【poj2104-求区间第k大数（不修改）】主席树/可持续化线段树

第一道主席树~然而是道比较水的。。。因为它不用修改。。。

转载一个让我看懂的主席树的讲解吧：http://blog.csdn.net/regina8023/article/details/41910615 （未授权，侵权删）

---------------------------------------------------------------------------------------------------------------------

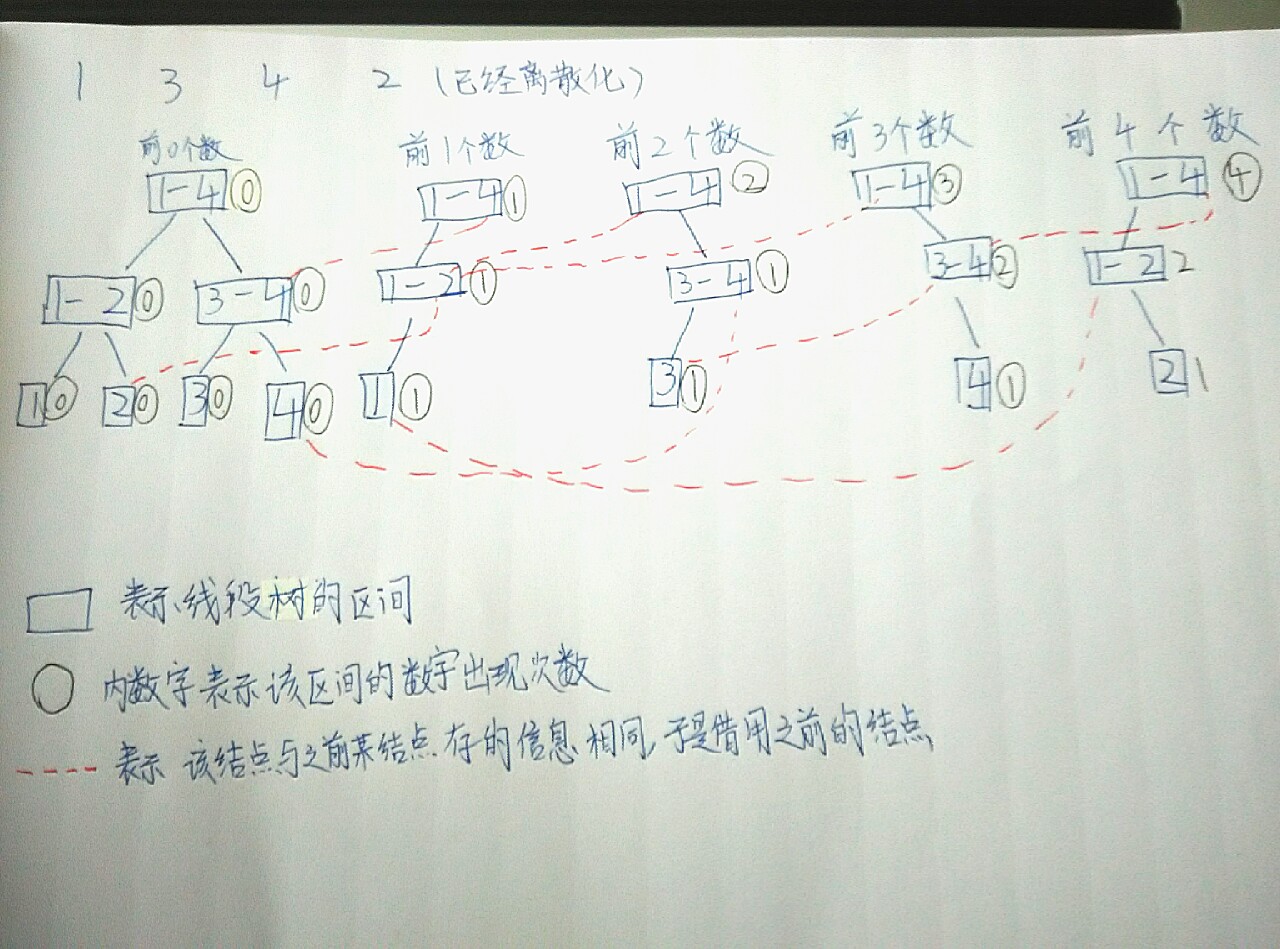
那么如果要询问i-j之间数字出现的次数怎么办呢？

因为每一棵线段树的区间都是相同的，所以要求l-r之间的数字的出现次数只要用前r位出现的次数减去前l-1位出现的次数，就是ans

但是如果有修改操作怎么办？

如果沿用上面的做法，那么修改操作是O(nlogn)的，查询是O(1)的，修改要花好长时间。。。

前缀和联想到了树状数组，那么将前缀和用树状数组维护的话修改是O(logn*logn)，查询时O(logn)，查询的时间虽然变长，但是修改的时间缩短许多！！

注意：

函数式线段树的数组要开大一点！！

---------------------------------------------------------------------------------------------------------------------

这题就是模版题啦，先离散，求区间第k大的时候lx=root[l-1],rx=root[r]，两边同时走不断作差，看看左孩子的数量，如果k更大就减掉左孩子的到有右孩子中找。

代码：

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 using namespace std;

 const int N=,INF=(int)1e9+;
 struct trnode{
     int lc,rc,cnt;
 }t[*N];
 struct node{
     int d,id;
 }p[N];
 int n,m,tl,mx;
 int a[N],num[N],root[N];

 bool cmp(node x,node y){return x.d<y.d;}

 int bt(int l,int r)
 {
     int x=++tl;
     // a[x].l=l;a[x].r=r;
     t[x].lc=t[x].rc=;
     t[x].cnt=;
     if(l<r)
     {
         int mid=(l+r)/;
         t[x].lc=bt(l,mid);
         t[x].rc=bt(mid+,r);
     }
     return x;
 }

 int add(int rt,int x)
 {
     int now=++tl,tmp=now;
     t[now].cnt=t[rt].cnt+;
     int l=,r=mx,mid;
     while(l<r)
     {
         mid=(l+r)/;
         if(x<=mid)
         {
             t[now].lc=++tl;
             t[now].rc=t[rt].rc;
             rt=t[rt].lc;
             now=tl;
             r=mid;
         }
         else
         {
             t[now].lc=t[rt].lc;
             t[now].rc=++tl;
             rt=t[rt].rc;
             now=tl;
             l=mid+;
         }
         t[now].cnt=t[rt].cnt+;
     }
     return tmp;
 }

 int query(int lx,int rx,int k)
 {
     int l=,r=mx,mid;
     while(l<r)
     {
         mid=(l+r)/;
         if(t[t[rx].lc].cnt-t[t[lx].lc].cnt>=k)
         {
             r=mid;
             lx=t[lx].lc;
             rx=t[rx].lc;
         }
         else
         {
             l=mid+;
             k-=t[t[rx].lc].cnt-t[t[lx].lc].cnt;
             lx=t[lx].rc;
             rx=t[rx].rc;
         }
     }
     return l;
 }

 void output(int x)
 {
     printf("x = %d  lc = %d  rc = %d  cnt = %d\n",x,t[x].lc,t[x].rc,t[x].cnt);
     if(t[x].lc) output(t[x].lc);
     if(t[x].rc) output(t[x].rc);
 }

 int main()
 {
     freopen("a.in","r",stdin);
     while(scanf("%d%d",&n,&m)!=EOF)
     {
         tl=;mx=;
         for(int i=;i<=n;i++)
         {
             scanf("%d",&a[i]);
             p[i].d=a[i];p[i].id=i;
         }
         sort(p+,p++n,cmp);
         p[].d=INF;
         for(int i=;i<=n;i++)
         {
             if(p[i].d!=p[i-].d) mx++,num[mx]=p[i].d;
             a[p[i].id]=mx;
         }
         root[]=bt(,mx);
         for(int i=;i<=n;i++)
             root[i]=add(root[i-],a[i]);
         // output(root[5]);
         for(int i=;i<=m;i++)
         {
             int l,r,k;
             scanf("%d%d%d",&l,&r,&k);
             printf("%d\n",num[query(root[l-],root[r],k)]);
         }
     }
     return ;
 }