图——图的Kruskal法最小生成树实现

1，最小生成树的特征：

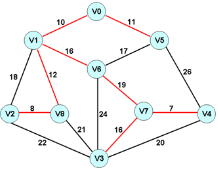
1，选取的边是图中权值较小的边；

2，所有边连接后不构成回路；

2，prim 算法是以顶点为核心的，最下生成树最大的特征是边，但 prim 算法非要以顶点为核心来进行，有些复杂和难以理解；

3，既然最小生成树关心的是如何选择 n - 1 条边，那么是否可以直接以边为核心进行算法设计？

4，简单尝试：

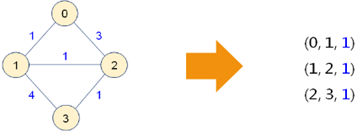
1，由 4 个顶点构成的图，选择 3 条权值最小的边；

2，还要设法避免回路；

5，需要解决的问题：

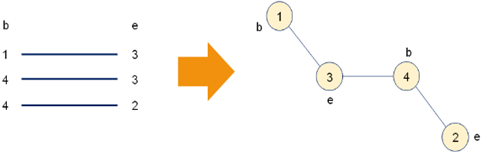
1，如何判断新选择的边与已选择的边是否构成回路？

6，技巧：前驱标记数组（避开新加入边造成回路问题）

1，定义数组：Array<int> p(vCount())；

2，定义数组元素的意义：

1，p[n] 表示顶点 n 在边的连接通路上的另一端顶点；

3，前驱标记数组究竟是怎么来的？

7，最小生成树算法的核心步骤（Kruskal）：

1，定义前驱标记数组：Array<int> p(vCount())；

2，获取当前图中的所有边，并存储于 edges 数组中；

3，对数组 deges 按照权值进行排序；

4，利用 p 数组在 edges 数组中选择前 n - 1 不构成回路的边；

8，Kruskal 算法流程：

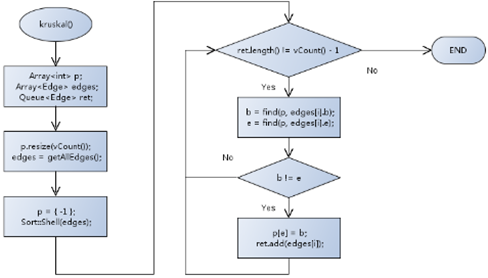
9，关键的 find 查找函数：

10，最小生成树算法 Kruskal （克鲁斯卡）实现：

 　　 /* 最小、大生成树的 kruskal 算法 */
     SharedPointer< Array< Edge<E> > > kruskal(const bool MINMUM = true)
     {
         LinkQueue< Edge<E> > ret;  // 返回的队列
         SharedPointer< Array< Edge<E> > > edges = getUndirectedEdges();  // 将无相图中的所有边都拿到
         DynamicArray<int> p(vCount());  // 前驱标记数组

         /* 设置前驱标记值 */
         for(int i=; i<p.length(); i++)
         {
             p[i] = -;
         }

         /* 对边数组排序 */
         Sort::Shell(*edges, MINMUM);  // 第二个参数对边进行从大到小的次序排序，用来生成最大生成树

         /* 进入循环，挑选边 */
         for(int i=; (i<edges->length()) && (ret.length() < (vCount()-)); i++)  // 最多循环边的个数次，且如果边很多但已经有 N - 1 条边被选择了，那么结束循环
 {
             int b = find(p, (*edges)[i].b);  // 在前驱标记数组中查找挑选的边的两个顶点
             int e = find(p, (*edges)[i].e);  // 前驱标记数组用于判断新选择的边是否会造成回路

             if( b != e)  // 相等会构成回路
             {
                 p[e] = b;  // 修改前驱标记数组

                 ret.add((*edges)[i]);  // 将这条边加入结果集合中去
             }
         }

         if( ret.length() != (vCount()-) )  // 判断边是否够，不够就不能构成最小生成树
         {
             THROW_EXCEPTION(InvalidOperationException, "No enough edges for Kruskal operation ...");
         }

         return toArray(ret);  // 将结果转换为数组
     }

11，Kruskal 算法测试代码：

 #include <iostream>
 #include "MatrixGraph.h"
 #include "ListGraph.h"

 using namespace std;
 using namespace DTLib;

 template< typename V, typename E >
 Graph<V, E>& GraphEasy()
 {
 　　 static MatrixGraph<, V, E> g;

     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
 　　 g.setEdge(, , );

     return g;
 }

 template< typename V, typename E >
 Graph<V, E>& GraphComplex()
 {
 　　 static ListGraph<V, E> g();

     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
     g.setEdge(, , );
 　　 g.setEdge(, , );

     return g;
 }

 int main()
 {
     Graph<int, int>& g = GraphEasy<int, int>();
 　　 SharedPointer< Array< Edge<int> > > sa = g.kruskal();  

 　　 int w = ;

     for(int i=; i<sa->length(); i++)
     {
         w += (*sa)[i].data;

         cout << (*sa)[i].b << " " << (*sa)[i].e << " " << (*sa)[i].data << endl;
 　　 }

 　　 cout << "Weight: " << w << endl;

     return ;
 }

13，小结：

1，Prim 算法以顶点为核心寻找最小生成树，不够直接；

2，Kruskal 算法以边为核心寻找最小生成树，直观简单；

3，Kruskal 算法中的关键是前驱标记数组的使用；

4，前驱标记数组用于判断新选择的边是否会造成回路；