Integer Partition（hdu4658）2013 Multi-University Training Contest 6 整数拆分二

Integer Partition

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 524 Accepted Submission(s): 238

Problem Description

Given n, k, calculate the number of different (unordered) partitions of n such that no part is repeated k or more times.

 

Input

First line, number of test cases, T. 
Following are T lines. Each line contains two numbers, n and k.

1<=n,k,T<=10⁵

 

Output

T lines, each line contains answer to the responding test case.
Since the numbers can be very large, you should output them modulo 10⁹+7.

 

Sample Input

4

4 2

4 3

4 4

4 5

 

Sample Output

2

4

4

5

 

Source

2013 Multi-University Training Contest 6

 

 

 

题目：http://acm.hdu.edu.cn/showproblem.php?pid=4658

题意：问一个数n能被拆分成多少种方法，且每一种方法里数字重复个数不能超过k（等于k）。

 

五边形数定理续，结合上一题（hdu4651），先打表，然后把大于k的个数剪掉；

 

 

好吧，再啰嗦一遍：

 

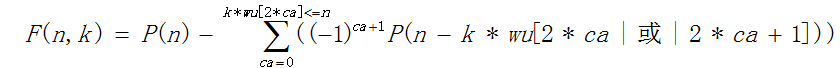
用了五边形数定理以及生成函数，然而我看懂了生成函数怎么搞这题却不知道为啥生成函数是五边形数形式= =

首先观察下面的图片：

很容易我们可以发现用这种方式构造N个五边形（假设一个点也算一个五边形），需要点的个数为：

n∗(3n−1)2

---

接下来我们来看一下数拆分。 
提问：将一个正整数N拆成不少于一个数的和，问有多少种方案。

很容易我们可以构造一个多项式： 
P(x)=(1+x1+x2+...)(1+x2+x4+...)(1+x3+x6+...)... 
=Px(0)x0+Px(1)x1+Px(2)x2+...+Px(n)xn

可以发现N的数拆分的方案数正对应着多项式展开后xn的系数Px(n)

考虑如下等式：

(1+x1+x2+...)=11−x

因此我们有：

∏i=0∞11−xi=∑i=0∞Px(i)xi

其中上式等式左边是欧拉函数ϕ(x)的倒数。即：

1ϕ(x)=∑i=0∞Px(i)xi

欧拉函数ϕ(x)的展开式为：

ϕ(x)=(1−x)(1−x2)(1−x3)...=1−x−x2+x5+x7−x12−x15+x22+x26−...

其中的x的指数正对应着广义五边形数！

n	0	1	-1	2	-2	3	-3	4	-4	…
P(n)	0	1	2	5	7	12	15	22	26	…

现在我们要计算Px(n)，由于1ϕ(x)=P(x)，亦即ϕ(x)P(x)=1。

(1−x−x2+x5+...)(Px(0)+Px(1)x+Px(2)x2+Px(3)x3+...)=1

所以：Px(n)=Px(n−1)+Px(n−2)−Px(n−5)−Px(n−7)+...

由于对于满足i(3i−1)2≤n的i的个数不超过(√n)个，于是计算所有Px(n)的复杂度为O(n(√n))

---

上面我们说明的是不带限制的数拆分，现在我们给定一个限制：拆分出来的每种数的个数不能大于等于k（这也是本题的要求）。

类似的，我们考虑生成函数：

(1+x1+x2+...+xk−1)(1+x2+x4+...x2(k−1))...=∏i=0∞1−xki1−xi=ϕ(xk)ϕ(x)=ϕ(xk)P(x)

展开ϕ(xk)得：

(1−xk)(1−x2k)(1−x3k)...=1−xk−x2k+x5k+x7k−x12k−x15k+...

然后可得：

ϕ(xk)P(x)=(1−xk−x2k+x5k...)(Px(0)+Px(1)x+Px(2)x2+Px(3)x3+...)

令Fk(n)表示n的满足数拆分时每种数的个数小于等于k的数拆分方案数。则有：

Fk(n)=Px(n)−Px(n−k)−Px(n−2k)+Px(n−5k)+...

 

一开始超时了，不然把取余的部分修改了下就过了。。。

 

 

卡过啊！

 

转载请注明出处：寻找&星空の孩子

 #include<iostream>
 #include<cstdio>
 #define NN 100005
 #define LL __int64
 #define mod 1000000007

 using namespace std;
 LL wu[NN],pa[NN];
 void init()
 {
     pa[]=;
     pa[]=;
     pa[]=;
     pa[]=;
     LL ca=;
     for(LL i=; i<=/; i++)
     {
         wu[ca++]=i*(*i-)/;
         wu[ca++]=i*(*i+)/;
         if(wu[ca-]>) break;
     }
     for(LL i=; i<=; i++)
     {
         pa[i]=(pa[i-]+pa[i-])%mod;
         ca=;
         while(wu[*ca]<=i)
         {
             if(ca&)
             {
                 pa[i]=(pa[i]-pa[i-wu[*ca]]);
                 pa[i]=(pa[i]%mod+mod)%mod;
                 if(wu[*ca+]<=i)
                     pa[i]=(pa[i]-pa[i-wu[*ca+]]),pa[i]=(pa[i]%mod+mod)%mod;
             }
             else
             {
                 pa[i]=(pa[i]+pa[i-wu[*ca]]);
                 pa[i]=(pa[i]%mod+mod)%mod;
                 if(wu[*ca+]<=i)
                     pa[i]=(pa[i]+pa[i-wu[*ca+]]),pa[i]=(pa[i]%mod+mod)%mod;
             }
             ca++;
         }
     }
 }
 LL work(int n,int k)
 {
     LL ans=pa[n];
     LL ca=;
     while(k*wu[*ca]<=n)
     {
         if(ca&)
         {
             ans=(ans+pa[n-k*wu[*ca]]);
             ans=(ans%mod+mod)%mod;
             if(k*wu[*ca+]<=n)
                 ans=(ans+pa[n-k*wu[*ca+]]),ans=(ans%mod+mod)%mod;
         }
         else
         {
             ans=(ans-pa[n-k*wu[*ca]]);
             ans=(ans%mod+mod)%mod;
             if(k*wu[*ca+]<=n)
                 ans=(ans-pa[n-k*wu[*ca+]]),ans=(ans%mod+mod)%mod;
         }
         ca++;
     }
     return ans;
 }
 int main()
 {
     int T,n,k;
     init();
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d",&n,&k);
         printf("%I64d\n",work(n,k));
     }
     return ;

 }

数论还有很多需要学习！