质心坐标(barycentric coordinates)及其应用

一、什么是质心坐标？

在几何结构中，质心坐标是指图形中的点相对各顶点的位置。

以图１的线段 AB 为例，点 P 位于线段 AB 之间，

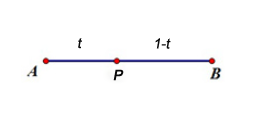
　　图１　线段AB和点P

此时计算点 P 的公式为 。

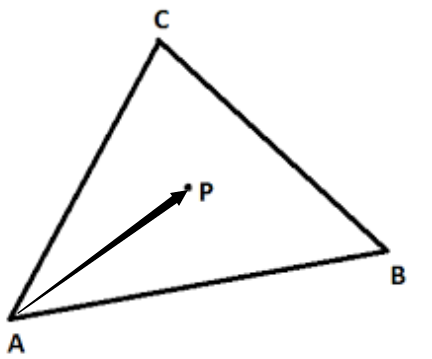
同理，在三角形 ABC 中，三角形内点 P 的计算公式为：——公式一。

公式一的最终表示形式为：

那么如何计算参数 m 和 n 呢？

下面给出推导过程：

根据公式一可得：

我们将  记作向量  ，将  记作向量  ， 将  记作向量 ，则公式为：

然后分别乘以 v0  和 v1 得到如下两个公式：

继续化解方程式得：

令：

继续化简方程式得：

根据莱布尼茨公式可得：

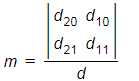
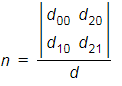
其中d =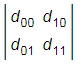 

二、质心坐标的应用

质心坐标的应用场景很多，可以用于：

• 判断一个点是否在三角形内
• 根据三角形三个顶点得到三角形内一个点P

三、代码实现

已知三角形的三个顶点，计算三角形内一个点 P 的代码实现：

//vPos1, vPos2,vPos3 分别代表三角形的三个顶点
//vP代表三角形内的一个点、
//fI代表 vPos1的系数
//fJ代表 vPos2的系数
//fK 代表 vPos3的系数
bool GetBarycentricCoord(vec2 vPos1, vec2 vPos2, vec2 vPos3, vec2 vP, float& fI, float& fJ, float& fK)
{
    // Compute vectors
    vec2 v0 = vPos2 - vPos1;
    vec2 v1 = vPos3 - vPos1;
    vec2 v2 = vP - vPos1;

    // Compute dot products
    float fDot00 = Dot(v0, v0);
    float fDot01 = Dot(v0, v1);
    float fDot02 = Dot(v0, v2);
    float fDot11 = Dot(v1, v1);
    float fDot12 = Dot(v1, v2);

    // Compute barycentric coordinates
    float fInvDenom =  / (fDot00 * fDot11 - fDot01 * fDot01);
    float fTempU = (fDot11 * fDot02 - fDot01 * fDot12) * fInvDenom;
    float fTempV = (fDot00 * fDot12 - fDot01 * fDot02) * fInvDenom;

    // Check if point is in triangle or edge
    bool bIsInTri = (fTempU >= ) && (fTempV >= ) && (fTempU + fTempV <= );
    if (bIsInTri)
    {
        fJ = fTempU;
        fK = fTempV;
        fI =  - fJ - fK;
    }
    return bIsInTri;
}