隐藏马尔科夫模型HMM

概率图模型

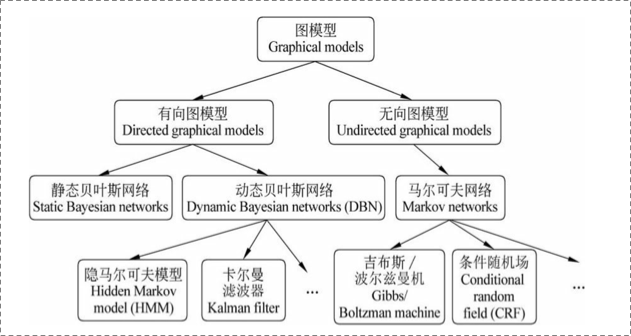
HMM

先从一个具体的例子入手,看看我们要解决的实际问题.例子引自wiki.https://en.wikipedia.org/wiki/Hidden_Markov_model

Consider two friends, Alice and Bob, who live far apart from each other and who talk together daily over the telephone about what they did that day. Bob is only interested in three activities: walking in the park, shopping, and cleaning his apartment. The choice of what to do is determined exclusively by the weather on a given day. Alice has no definite information about the weather, but she knows general trends. Based on what Bob tells her he did each day, Alice tries to guess what the weather must have been like.

Alice believes that the weather operates as a discrete Markov chain. There are two states, "Rainy" and "Sunny", but she cannot observe them directly, that is, they are hidden from her. On each day, there is a certain chance that Bob will perform one of the following activities, depending on the weather: "walk", "shop", or "clean". Since Bob tells Alice about his activities, those are the observations. The entire system is that of a hidden Markov model (HMM).

简单翻译一下：Alice和Bob住在两地,每天电话沟通.Bob只对三件事有兴趣:逛公园,购物,打扫房间.Bob根据天气安排自己每日的活动.Alice知道bob每天都干嘛,以此为基础,她可以推测出Bob所在地区的天气.Alice认为天气预测就是一个马尔科夫链.天气有两种状态,Rainy/Sunny,由于她无法直接观测到天气状态,天气对她而言是隐藏的.

马尔科夫假设：

假设模型的当前状态仅仅依赖于前面的几个状态，这被称为马尔科夫假设，它极大地简化了问题。显然，这可能是一种粗糙的假设，并且因此可能将一些非常重要的信息丢失。

一个马尔科夫过程是状态间的转移仅依赖于前n个状态的过程。这个过程被称之为n阶马尔科夫模型，其中n是影响下一个状态选择的（前）n个状态。

最简单的马尔科夫过程是一阶模型，它的状态选择仅与前一个状态有关.

比如今天的天气和昨天的天气有关.如下：

隐藏马尔科夫

回到我们的例子,当我们有足够多的天气资料以后,我们是可以根据昨天的天气推测出最有可能的的今天的天气的.比如昨天晴天,那求p(晴天|晴天),p(阴天|晴天)的概率,取二者之中较大的一个即可.

这个例子里天气状况我们称之为状态,相应的概率矩阵称之为状态转移矩阵.一个有M个状态的马尔科夫模型有\(M^2\)个状态转移.

现在我们定义一个一阶马尔科夫过程如下：状态：三个状态——晴天，多云，雨天。 pi向量：定义系统初始化时每一个状态的概率。状态转移矩阵：给定前一天天气情况下的当前天气概率。

任何一个可以用这种方式描述的系统都是一个马尔科夫过程。

但是考虑我们的例子中,Alice虽然每日与Bob通话,但是Bob并不会告诉他当地天气情况,只会告诉他自己每天干了啥(逛公园/购物/打扫房间等).所以天气状态对Alice来说是隐藏(Hidden)的,Alice并不知道每日天气,他能事先知道的只有阴天后,第二天是阴天/晴天的概率,即状态转移矩阵。

天气状态是隐藏状态,Bob的每日活动(逛公园/购物/打扫房间)是观察状态.

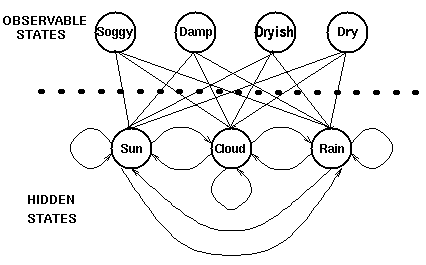
图文不符,凑合看,领会意图....假装soggy/damp/...代表逛公园/购物/打扫房间....

对每一种隐藏状态,都有与之对应的观测状态,和前面的状态转移概率矩阵一样,我们有如下的概率矩阵称之为混淆矩阵：

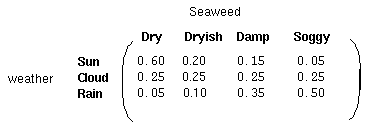
至此,一个HMM模型所包含的要素如下：

隐藏状态
观测状态
pi向量模型初始隐藏状态的概率
转移矩阵：状态转移的概率矩阵
混淆矩阵(有的翻译成发射概率矩阵)：隐藏状态与观察状态的对应概率矩阵

alice预测bob所在地区天气用HMM建模可以表达如下：

 #隐藏状态

 states = ('Rainy', 'Sunny')

 #观测状态

 observations = ('walk', 'shop', 'clean')

 #初始pi向量

 start_probability = {'Rainy': 0.6, 'Sunny': 0.4}

 #状态转移矩阵

 transition_probability = {

    'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3},

    'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6},

    }

 #混淆矩阵.比如如下数据代表阴天时,bob有0.1的概率逛公园,0.4的概率散步,0.5的概率做清洁.

 emission_probability = {

    'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5},

    'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1},

    }

HMM解决的三个基本问题

给定HMM求一个观察序列的概率（评估）使用前向算法解决
搜索最有可能生成一个观察序列的隐藏状态序列（解码）使用维特比算法解决
是给定观察序列生成一个HMM（学习）使用前向-后向算法解决

对应到alice-bob的例子里即我们通过大量样本的训练已经得到了一个HMM的model.

Alice和Bob通了三天电话后发现第一天Bob去散步了，第二天他去购物了，第三天他清理房间了。Alice现在有两个问题：

这个观察序列“散步、购物、清理”的总的概率是多少？(注：这个问题对应于HMM的基本问题之一：已知HMM模型λ及观察序列O，如何计算P(O|λ)？)
最能解释这个观察序列的状态序列（晴/雨）又是什么？（注：这个问题对应HMM基本问题之二：给定观察序列O=O1,O2,…OT以及模型λ,如何选择一个对应的状态序列S = q1,q2,…qT，使得S能够最为合理的解释观察序列O？）
至于HMM的基本问题之三：如何调整模型参数, 使得P(O|λ)最大？这个问题事实上就是给出很多个观察序列值，来训练以上几个参数的问题。

算法

前向算法
维特比算法
前向-后向算法

HMM应用

词性标注
中文分词

HMM与CRF关系

比如要给"i love you"进行词性标注.

那么HMM中的"隐藏状态"即为词性(名词/动词/形容词/...)

HMM中的"观测状态"即为我们看到的具体的词(i/love/you)

实际上我们要做的就是求解p(l,s)哪种l使其最大？

其中s="i love u",对l1=(名词/动词/名词),我们可以计算出一个p1=p(l1,s),对l2=(名词/名词/名词),我们可以计算出一个p2=p(l2,s).自然地,对一个模型来说,应该算出的是p1>p2. 那么我们就把"i love u"标注为"名词/动词/名词"

如何计算p(l,s)

还是以上面的"i love u"为例,l=(名词/动词/名词)

p(li|li−1) 状态转移概率 (比如l2=动词,l1=名词,则代表名词后面接动词的概率);
p(wi|li) 发射概率(也就是之前例子里说的混淆矩阵概率) (比如l2=动词 w2="love" 代表一个动词是单词"love"的概率)

注意我们在条件随机场https://www.cnblogs.com/sdu20112013/p/10370334.html里提到的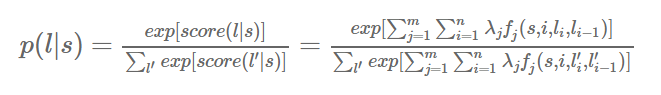

对一个HMM来说,对概率取对数可得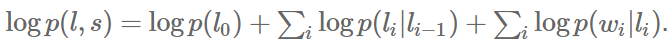

我们可以构建一个等价于该HMM的CRF

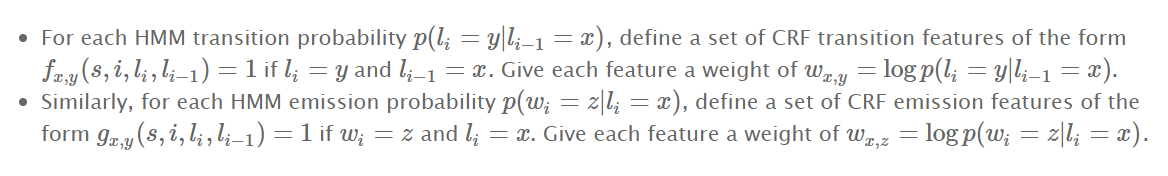
对每一个状态转移概率,都可以创建一个特征函数f,给一个权重w
对每一个发射概率,也可以定一个特征函数g,给一个权重w

这样crf计算出来的p(l,s)和HMM计算出来的p(l,s)就等价了.

也就是说每一个HMM都可以用某一个CRF来表达

crf比HMM更强大

crf可以定制更多的特征函数比如对"is that ok?"做词性标注.用crf的话,我们可以定义一个特征函数：一个以?结尾的句子的第一个单词更可能是动词. 在HMM中我们没办法表达这个信息. 从而crf的标注的准确率可以更高.
crf可以有更多样的权重. hmm里权重是可以任意的,正的,负的都可以.