堆排、python实现堆排

一、堆-完全二叉树

• 堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，是不稳定排序

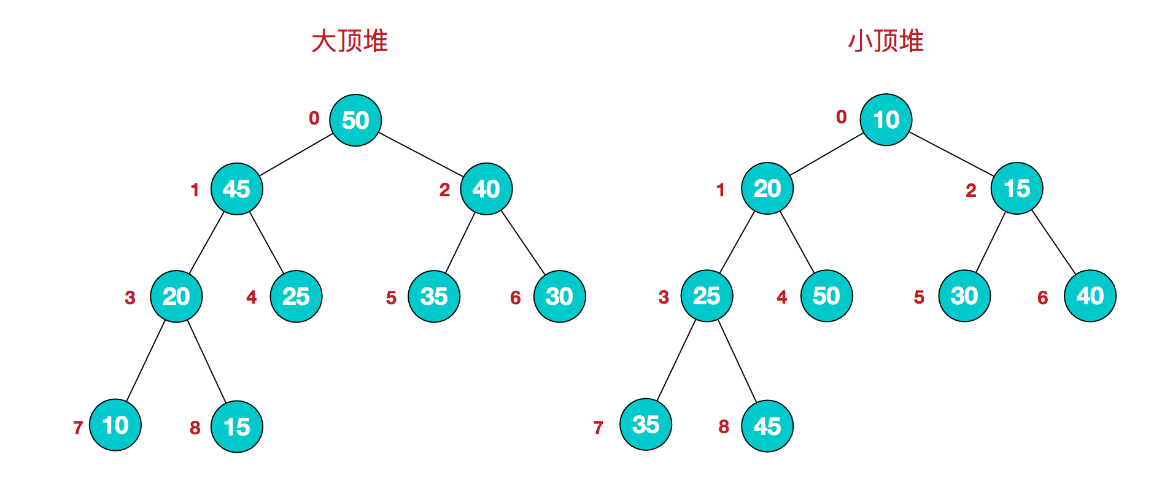
• 堆排序中的堆有大顶堆、小顶堆两种。他们都是完全二叉树
  
  

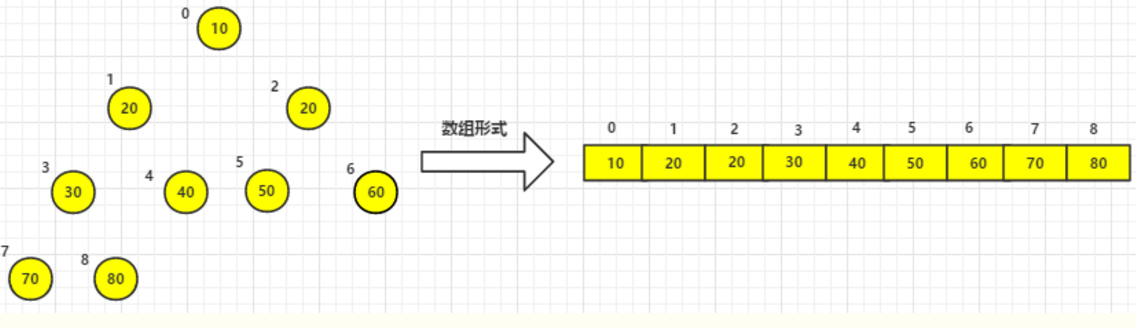
• 将该堆按照排序放入列表
  
  

1. 大顶堆：

所有的父节点的值都比孩子节点大，叶子节点值最小。root 根节点是第一个节点值最大

2. 小顶堆：

和大顶堆相反，所有父节点值，都小于子节点值，root 根节点是 第一个节点值最小

 

二、堆排序

• 基本思路：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。可称为有序区，然后将剩余n-1个元素重新构造成一个堆，估且称为堆区(未排序)。这样会得到n个元素的次小值。重复执行，有序区从:1--->n，堆区：n-->0，便能得到一个有序序列了
  
   

2.1 构造大顶堆

• 在构造有序堆时，开始时只需要扫描一半的元素（所有父节点）（length/2-1 --> 0）
  
  因为只有他们才有子节点：3-->2 -->1 -->0
  
  

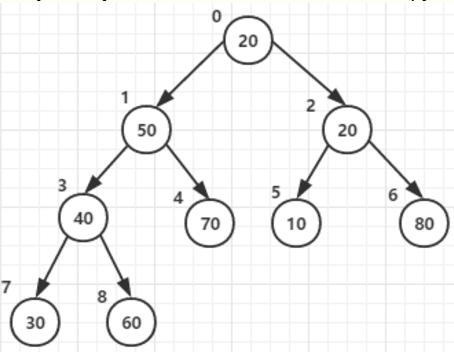
1. 从最后一个父节点开始，将父节点、他所有的子节点中的最大值交换到父节点。父节点：3

2. 将倒数第二个父节点同理交换，父节点：2

3. 父节点：1

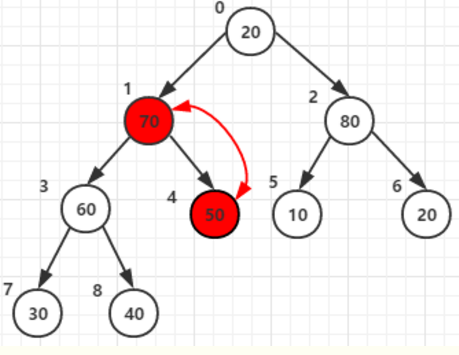
4. 根节点：0

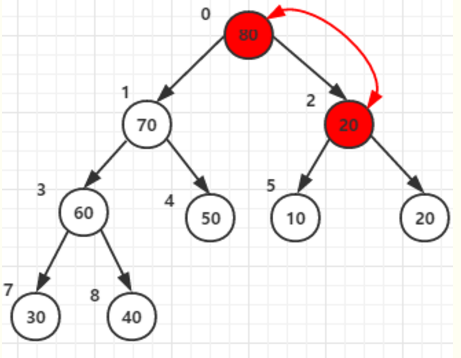
5. 注意很重要：务必注意-承接第3步。

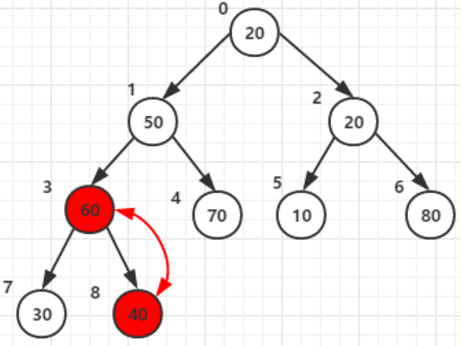
假设根节点值为：10， 当他和两个子节点70， 80，



 

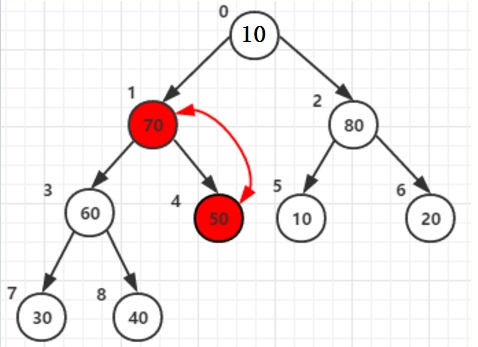
父节点和两子节点中的大的(80)交换后位于父节点2：原来80的位置。



 

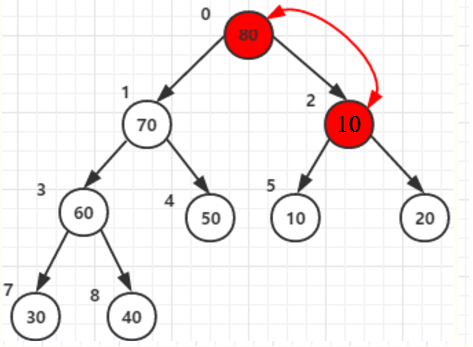
可是他还有子节点，且子节点中的值比根节点大，那就还需要以他为父节点构造一次，与子节点6 值为20交换一次



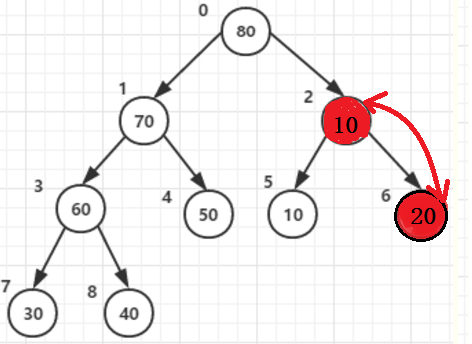
同理在其他所有父节点的构造中都需要判断调整

• 忽略第五步。构造好的的大顶堆如下:

 

2.2 开始排序

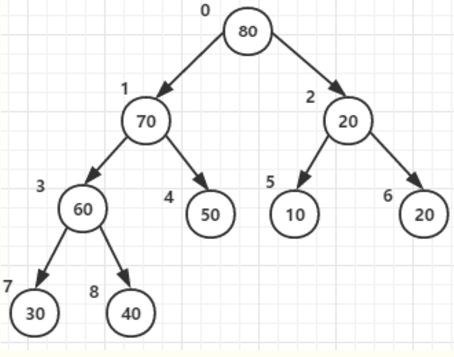
• 基本思路：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。可称为有序区，然后将剩余n-1个元素重新构造成一个堆，估且称为堆区(未排序)。这样会得到n个元素的次小值。重复执行，有序区从:1--->n，堆区：n-->0，便能得到一个有序序列了

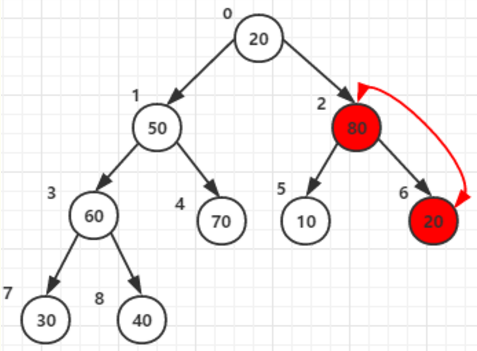
• 每次将堆顶（根节点）最的的元素和堆尾列表最后一个元素交换，80 和40交换
  
  即上面说的堆区(未排序)：n-->0最大元素（根节点），和有序区从:1--->n，最后一个元素交换
  
  

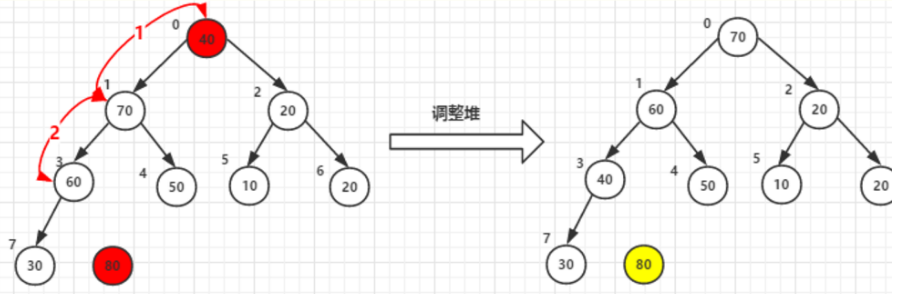
• 按照上面原理继续排序，70， 30 交换。然后调整堆
  
  

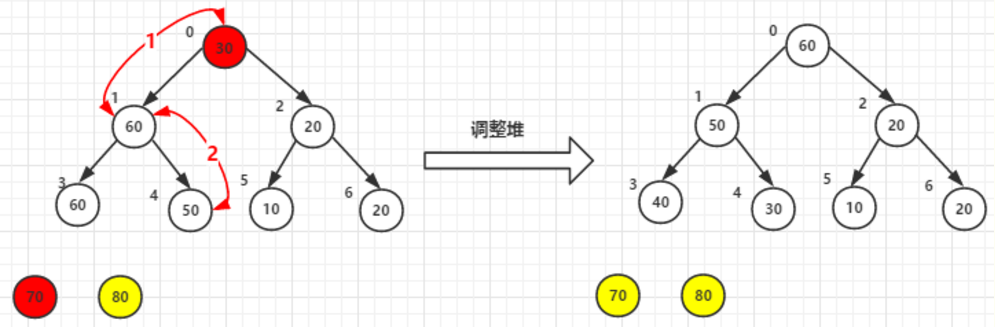
• 堆顶元素60尾元素20交换后-->调整堆
  
  

• 最后结果
  
  

三、Python代码实现

• 现在排序这么一个序列：list_ = [4, 7, 0, 9, 1, 5, 3, 3, 2, 6]

"""
堆排序  heap_sort

                     4
                   /   \
                 7      0
               /  \    / \
             9    1   5   3
           / \   /
         3   2  6

list_ = [4, 7, 0, 9, 1, 5, 3, 3, 2, 6]
"""

 

3.2 代码实现

def swap(data, root, last):
    data[root], data[last] = data[last], data[root]

#调整父节点 与孩子大小， 制作大顶堆
def adjust_heap(data, par_node, high):

    new_par_node = par_node
    j = 2*par_node +1   #取根节点的左孩子， 如果只有一个孩子 high就是左孩子，如果有两个孩子 high 就是右孩子

    while j <= high: #如果 j = high 说明没有右孩子，high就是左孩子
        if j < high and data[j] < data[j+1]: #如果这儿不判断 j < high 可能超出索引
            # 一个根节点下，如果有两个孩子，将 j  指向值大的那个孩子
            j += 1
        if data[j] > data[new_par_node]: #如果子节点值大于父节点，就互相交换
            data[new_par_node], data[j] = data[j], data[new_par_node]
            new_par_node = j #将当前节点，作为父节点，查找他的子树
            j = j * 2 + 1

        else:
            # 因为调整是从上到下，所以下面的所有子树肯定是排序好了的，
            #如果调整的父节点依然比下面最大的子节点大，就直接打断循环，堆已经调整好了的
            break

# 索引计算: 0 -->1 --->....
#    父节点 i   左子节点：2i +1  右子节点：2i +2  注意：当用长度表示最后一个叶子节点时 记得 -1
#    即 2i + 1 = length - 1 或者 2i + 2 = length - 1
#    2i+1 + 1 = length 或 2i+2 + 1 = length
#    2(i+1)=length 或 2(i+1）+1 = length
#    设j = i+1  则左子节点(偶数)：2j = length 和 右子节点(基数)：2j+1 = length
#    2j//2 = j == (2j+1)//2 这两个的整除是一样的，所以使用length//2 = j 然后 i + 1 = j
#    i = j-1  = length//2 -1  #注意左子节点:2i+1 //2 =i  而右子节点：(2i+2)//2 = i+1 

# 从第一个非叶子节点(即最后一个父节点)开始，即 list_.length//2 -1（len(list_)//2 - 1）

# 开始循环到 root 索引为：0 的第一个根节点， 将所有的根-叶子 调整好，成为一个 大顶堆
def heap_sort(lst):
    """
    根据列表长度，找到最后一个非叶子节点，开始循化到 root 根节点，制作 大顶堆
    :param lst: 将列表传入
    :return:
    """
    length = len(lst)
    last = length -1  #最后一个元素的 索引
    last_par_node = length//2 -1

    while last_par_node >= 0:

        adjust_heap(lst, last_par_node, length-1)
        last_par_node -= 1  #每调整好一个节点，从后往前移动一个节点

    # return lst

    while last > 0:
        #swap(lst, 0, last)
        lst[0], lst[last] = lst[last],lst[0]
        # 调整堆让 adjust 处理，最后已经排好序的数，就不处理了
        adjust_heap(lst, 0, last-1)
        last -= 1

    return lst #将列表返回

if __name__ == '__main__':
    list_ = [4, 7, 0, 9, 1, 5, 3, 3, 2, 6]
    heap_sort(list_)
    print(list_)

#最后结果为：
[0, 1, 2, 3, 3, 4, 5, 6, 7, 9]