BZOJ4356Ceoi2014 Wall——堆优化dijkstra+最短路树

题目描述

给出一个N*M的网格图，有一些方格里面存在城市，其中首都位于网格图的左上角。你可以沿着网络的边界走，要求你走的路线是一个环并且所有城市都要被你走出来的环圈起来，即想从方格图的外面走到任意一个城市一定要和你走的路线相交。你沿着方格的边界走是需要费用的，不同的边界费用可能不同，求最小代价。

1<=N,M<=400,走过边界的代价为正整数且不超过10^9

输入

输出

样例输入

Input 1
3 3
1 0 0
1 0 0
0 0 1
1 4 9 4
1 6 6 6
1 2 2 9
1 1 1
4 4 4
2 4 2
6 6 6

input 2
3 3
1 0 1
0 0 0
0 1 0
2 1 1 3
5 6 1 1
2 1 1 3
2 1 1
3 4 1
4 1 1
5 1 2

样例输出

output 1
38
output 2
22

提示

首先我们求出首都(即左上角)到每个城市左上角那个点的最短路形成的最短路树，那么有一个结论：所选的环一定将最短路树上的边圈在里面。

因为如果有一些最短路的边在环外，那么将环被这段最短路包含的部分换成这段最短路答案一定不会变劣。

所以我们现在就是要求在环不穿过城市和最短路树上的边的情况下最小。

我们将原图的每个点拆成四个点，如图所示。

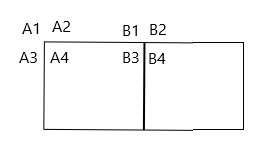
即将每个点拆成左上、左下、右上、右下四个点。

对于每个原图点拆成的四个点中每对相邻点，只要他们两个之间的边不是城市边或最短路树上的边，那么就将他们两个连一条边权为$0$的边。

特别注意的是原图左上角那个点拆成的$1$号点不与$2,3$号点连边(原因下面会提到)。

对于原图每条边两侧的两对点(例如$A2,B1$和$A4,B3$)分别将他们连边，边权为原图这条边的边权。

这样我们跑出从左上角$3$号点到$2$号点的最短路即为答案。

因为连边时不穿过城市边和最短路树上的边，且起点保证在这些边的外围，所以能将所有城市都圈在环内。

而从$3$号点跑最短路到$2$号点保证它是一个环且最短。不允许穿过最短路树边相当于将每个城市与起点连通。

#include<set>
#include<map>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<cstdio>
#include<bitset>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define pr pair<ll,int>
#define PR pair<int,int>
using namespace std;
int vis[410][410];
int num;
int sum;
int n,m;
int head[650000];
ll d[650000];
int to[5200000];
int next[5200000];
int val[5200000];
int v[650000];
int w[410][410][5];
int tot;
int x,y;
int mp[400000];
inline void add(int x,int y,int z)
{
	next[++tot]=head[x];
	head[x]=tot;
	to[tot]=y;
	val[tot]=z;
}
inline int get(int x,int y)
{
	x++,y++;
	return (x-1)*(m+1)+y;
}
inline void back(int num,int &x,int &y)
{
	x=(num-1)/(m+1)+1;
	y=num-(m+1)*(x-1);
	x--,y--;
}
namespace build
{
	int head[170000];
	ll d[170000];
	int from[170000];
	int vis[170000];
	int to[680000];
	int next[680000];
	int val[680000];
	int tot;
	inline void add(int x,int y,int z)
	{
		next[++tot]=head[x];
		head[x]=tot;
		to[tot]=y;
		val[tot]=z;
	}
	inline void dijkstra()
	{
		priority_queue< pr,vector<pr>,greater<pr> >q;
		for(int i=1;i<=num;i++)
		{
			d[i]=1ll<<60;
		}
		d[1]=0;
		q.push(make_pair(d[1],1));
		while(!q.empty())
		{
			int x=q.top().second;
			q.pop();
			if(vis[x])
			{
				continue;
			}
			vis[x]=1;
			for(int i=head[x];i;i=next[i])
			{
				if(d[to[i]]>d[x]+1ll*val[i])
				{
					d[to[i]]=d[x]+1ll*val[i];
					from[to[i]]=x;
					q.push(make_pair(d[to[i]],to[i]));
				}
			}
		}
	}
}
inline void dijkstra()
{
	priority_queue< pr,vector<pr>,greater<pr> >q;
	for(int i=1;i<=num*4;i++)
	{
		d[i]=1ll<<60;
	}
	d[num+1]=0;
	q.push(make_pair(d[num+1],num+1));
	while(!q.empty())
	{
		int now=q.top().second;
		q.pop();
		if(v[now])
		{
			continue;
		}
		v[now]=1;
		for(int i=head[now];i;i=next[i])
		{
			if(d[to[i]]>d[now]+1ll*val[i])
			{
				d[to[i]]=d[now]+1ll*val[i];
				q.push(make_pair(d[to[i]],to[i]));
			}
		}
	}
	printf("%lld",d[num*2+1]);
}
inline int find(int x,int y)
{
	if(x>y)
	{
		swap(x,y);
	}
	int a,b,c,d;
	back(x,a,b);
	back(y,c,d);
	if(b==d)
	{
		return (c-1)*(m+1)+d+1;
	}
	else
	{
		return sum+c*m+d;
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	num=(n+1)*(m+1);
	sum=n*(m+1);
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&vis[i][j]);
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			scanf("%d",&x);
			build::add(get(i-1,j),get(i,j),x);
			build::add(get(i,j),get(i-1,j),x);
			w[i-1][j][3]=w[i][j][1]=x;
		}
	}
	for(int i=0;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&x);
			build::add(get(i,j-1),get(i,j),x);
			build::add(get(i,j),get(i,j-1),x);
			w[i][j-1][2]=w[i][j][4]=x;
		}
	}
	build::dijkstra();
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(!vis[i-1][j-1]&&!vis[i-1][j]&&!vis[i][j-1]&&vis[i][j])
			{
				for(x=get(i-1,j-1);x!=1;x=build::from[x])
				{
					mp[find(build::from[x],x)]=1;
				}
			}
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(vis[i][j])
			{
				mp[find(get(i,j),get(i-1,j))]=1;
				mp[find(get(i,j),get(i,j-1))]=1;
				mp[find(get(i-1,j-1),get(i,j-1))]=1;
				mp[find(get(i-1,j-1),get(i-1,j))]=1;
			}
		}
	}
	for(int i=1;i<=num;i++)
	{
		back(i,x,y);
		if((!y||!mp[find(get(x,y),get(x,y-1))])&&i!=1)
		{
			add(i,2*num+i,0);
			add(2*num+i,i,0);
		}
		if((!x||!mp[find(get(x,y),get(x-1,y))])&&i!=1)
		{
			add(i,num+i,0);
			add(num+i,i,0);
		}
		if(x==n||!mp[find(get(x,y),get(x+1,y))])
		{
			add(num*2+i,num*3+i,0);
			add(num*3+i,num*2+i,0);
		}
		if(y==m||!mp[find(get(x,y),get(x,y+1))])
		{
			add(num+i,num*3+i,0);
			add(num*3+i,num+i,0);
		}
		if(y)
		{
			add(i,num+get(x,y-1),w[x][y][4]);
			add(num*2+i,num*3+get(x,y-1),w[x][y][4]);
		}
		if(x)
		{
			add(i,num*2+get(x-1,y),w[x][y][1]);
			add(num+i,num*3+get(x-1,y),w[x][y][1]);
		}
		if(x!=n)
		{
			add(num*2+i,get(x+1,y),w[x][y][3]);
			add(num*3+i,num+get(x+1,y),w[x][y][3]);
		}
		if(y!=m)
		{
			add(num+i,get(x,y+1),w[x][y][2]);
			add(num*3+i,num*2+get(x,y+1),w[x][y][2]);
		}
	}
	dijkstra();
}