[APIO2016]烟火表演

题目描述

https://www.lydsy.com/JudgeOnline/problem.php?id=4585

题解

这题太神了。

我们可以先列出一个dp方程，dp[x][d]表示x节点到所有叶子的距离的d时的代价。

结论1：对于每个点来说，这个dp数组为二维平面上是一个下凸函数。

证明：对于叶子来说一定成立，在w[x]处为0，然后小于w[x]的部分斜率为-1，大与w[x]的部斜率为1。

对于非叶子节点 ，它的函数时有儿子们加起来的，也成立。

然后我们考虑一个点如何向父亲转移。

这是要分四种情况，假设当前节点的斜率为0的部分为L~R。

x<=L f'(x)=f(x)+w[u]

因为边权不能为负，所以我们只能从小的地方往大的地方转移。

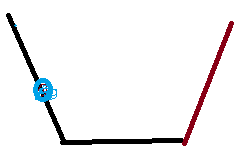
比如这个蓝点，它只能从它以及前面的地方转移，但从自己转移时最优的。

x>=L&&x<=L=w[u] f'(x)=f(L)+w-(x-L)

在L处答案为f(L)+w，没往右动一格代价会-1。

x>=L+w[u]&&x<=R+w[u] f'(x)=f(L)

这个相当于直接转移了，没有代价。

x>=R+w[u] f'(x)=f(x)+(x-R)-w

相当于是走过了，会产生代价。

我们发现转移大概长这样(继续盗图)。

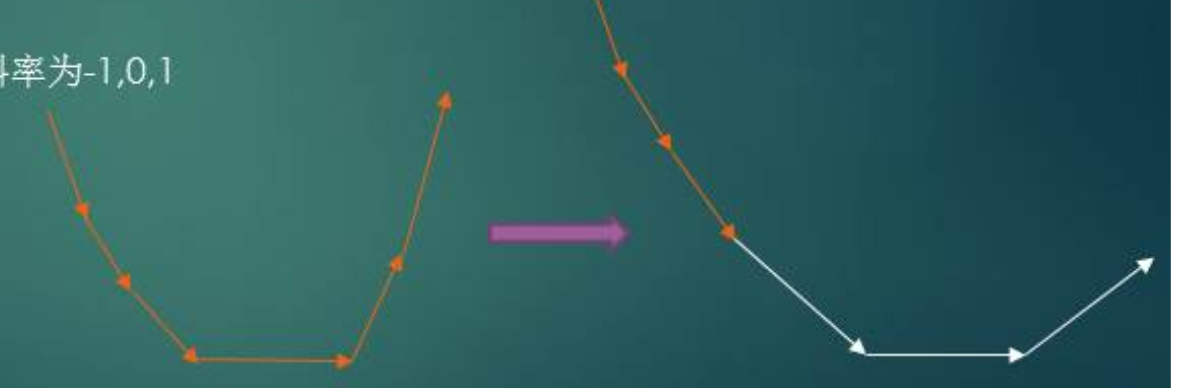
我们把左边的点向上动一段后插入斜率为-1的线，再把斜率为0的部分向右平移，最后面是斜率为1的线。

然后这种操作就可以维护了。

思路大概就是只维护拐点，用一个可并堆，每次把右边的部分弹掉。

结论2：每次合并到一个非叶子节点时，斜率为0的线右边有n个点，n为该点的儿子数。

证明：因为最后那一块斜率一定为n(n个斜率为1的直线相加)，然后往前经过一个拐点，斜率会-1。

然后把LR取出来做平移，再插回去，最后一直合并到1。

结论3：每经过一个拐点，斜率-1(其实它和上面的结论一个意思)。

然后就可以利用最后的拐点直接算答案了。

怎么算呢？我们把斜率>=0的直线弹掉，把前面的所有直线斜率+1，那么每条直线都会产生deltax的代价，总共有xn的代价，那我们就在答案里+xn，此时最后一条直线斜率为0，把它删掉。

然后一直做，最后得到的是f(0)-f(min)，f(0)就是所有边权之和，那么f(min)就可以求出来了。

代码

#include<iostream>
#include<cstdio>
#define N 600002
using namespace std;
typedef long long ll;
int deep[N],d[N],n,m,fa[N],T[N],tot;
ll sum,w[N];
inline ll rd(){
    ll x=;char c=getchar();bool f=;
    while(!isdigit(c)){if(c=='-')f=;c=getchar();}
    while(isdigit(c)){x=(x<<)+(x<<)+(c^);c=getchar();}
    return f?-x:x;
}
struct tr{
    ll v;int l,r;
}tr[N];
int merge(int x,int y){
    if(!x||!y)return x^y;
    if(tr[x].v<tr[y].v)swap(x,y);
    tr[x].r=merge(tr[x].r,y);
    if(deep[tr[x].l]<deep[tr[x].r])swap(tr[x].l,tr[x].r);
    deep[x]=deep[tr[x].r]+;
    return x;
}
inline int pop(int x){return merge(tr[x].l,tr[x].r);}
int main(){
    n=rd();m=rd();
    for(int i=;i<=n+m;++i){
        fa[i]=rd();w[i]=rd();sum+=w[i];d[fa[i]]++;
    }
    for(int i=n+m;i>=;--i){
        ll l=,r=;
        if(i<=n){
            while(--d[i])T[i]=pop(T[i]);
            l=tr[T[i]].v;T[i]=pop(T[i]);
            r=tr[T[i]].v;T[i]=pop(T[i]);
        }
        tr[++tot].v=l+w[i];tr[++tot].v=r+w[i];
        T[i]=merge(T[i],merge(tot-,tot));
        T[fa[i]]=merge(T[fa[i]],T[i]);
    }
    while(d[]--)T[]=pop(T[]);
    while(T[]){sum-=tr[T[]].v;T[]=pop(T[]);}
    cout<<sum;
    return ;
}