快速傅里叶变换(FFT)_转载

FFTFFT·Fast  Fourier  TransformationFast  Fourier  Transformation快速傅立叶变换

P3803 【模板】多项式乘法（FFT） 参考上文

首先介绍, 欧拉公式:

公式描述：公式中e是自然对数的底，i是虚数单位。

快速傅里叶变换(FFT)详解

前言:

DFT：离散傅里叶变换—>O(n²)计算多项式乘法

FFT：快速傅里叶变换—>O(n∗log(n)O(n∗log⁡(n)计算多项式乘法

FNTT/NTT：快速傅里叶变换的优化版—>优化常数及误差

FWT：快速沃尔什变换—>利用类似FFT的东西解决一类卷积问题

MTT：毛爷爷的FFT—>非常nb/任意模数

FMT 快速莫比乌斯变化—>感谢stump提供

多项式

系数表示法

设A(x)A(x)表示一个n−1次多项式则

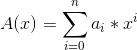
例如：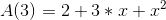

利用这种方法计算多项式乘法复杂度为O(n²)

（第一个多项式中每个系数都需要与第二个多项式的每个系数相乘）

点值表示法

将nn互不相同的xx带入多项式，会得到nn个不同的取值yy

则该多项式被这n个点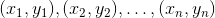唯一确定

其中:

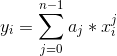
例如：上面的例子用点值表示法可以为(0,2),(1,6),(2,12)

利用这种方法计算多项式乘法的时间复杂度仍然为O(n²)

（选点O(n)，每次计算O(n))

我们可以看到，两种方法的时间复杂度都为O(n²)，我们考虑对其进行优化

对于第一种方法，由于每个点的系数都是固定的，想要优化比较困难

对于第二种方法，貌似也没有什么好的优化方法，不过当你看完下面的知识，或许就不这么想了

复数

在介绍复数之前，首先介绍一些可能会用到的东西

向量

同时具有大小和方向的量

在几何中通常用带有箭头的线段表示

圆的弧度制

等于半径长的圆弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度。用弧度作单位来度量角的制度叫做弧度制

公式:

    ,      

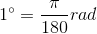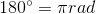
弧度和角度一样均有正负，逆时针为正，顺时针为负 

π就是逆时针180°，-π就是顺时针180°

单位根

欧拉公式

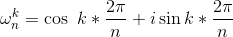
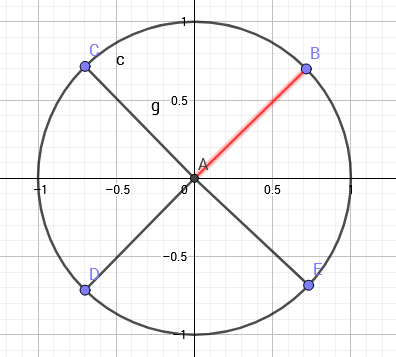
图中向量AB表示的复数为8次单位根.

在代数中，若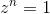,我们把z称为n次单位根.

单位根的性质

快速傅里叶变换

快速傅里叶逆变换

这样我们就得到点值与系数之间的表示啦.

理论总结

至此，FFT的基础理论部分就结束了。

我们来小结一下FFT是怎么成功实现的

首先，人们在用系数表示法研究多项式的时候遇阻

于是开始考虑能否用点值表示法优化这个东西。

然后根据复数的两条性质（这个思维跨度比较大）得到了一种分治算法。

最后又推了一波公式，找到了点值表示法与系数表示法之间转换关系。

其实FFT的实现思路大概就是

系数表示法—>点值表示法—>系数表示法

引用一下远航之曲大佬的图

当然，再实现的过程中还有很多技巧

我们根据代码来理解一下

递归实现

递归实现的方法比较简单。

就是按找我们上面说的过程，不断把要求的序列分成两部分，再进行合并

在c++的STL中提供了现成的complex类，但是我不建议大家用，毕竟手写也就那么几行，而且万一某个毒瘤卡STL那岂不是很ＧＧ

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int MAXN=2*1e6+10;
inline int read()
{
    char c=getchar();int x=0,f=1;
    '){if(c=='-')f=-1;c=getchar();}
    ';c=getchar();}
    return x*f;
}
const double Pi=acos(-1.0);
struct complex
{
    double x,y;
    complex (double xx=0,double yy=0){x=xx,y=yy;}
}a[MAXN],b[MAXN];
complex operator + (complex a,complex b){ return complex(a.x+b.x , a.y+b.y);}
complex operator - (complex a,complex b){ return complex(a.x-b.x , a.y-b.y);}
complex operator * (complex a,complex b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}//不懂的看复数的运算那部分
void fast_fast_tle(int limit,complex *a,int type)
{
    if(limit==1) return ;//只有一个常数项
    complex a1[limit>>1],a2[limit>>1];
    for(int i=0;i<=limit;i+=2)//根据下标的奇偶性分类
        a1[i>>1]=a[i],a2[i>>1]=a[i+1];
    fast_fast_tle(limit>>1,a1,type);
    fast_fast_tle(limit>>1,a2,type);
    complex Wn=complex(cos(2.0*Pi/limit) , type*sin(2.0*Pi/limit)),w=complex(1,0);
    //Wn为单位根，w表示幂
    for(int i=0;i<(limit>>1);i++,w=w*Wn)//这里的w相当于公式中的k
        a[i]=a1[i]+w*a2[i],
        a[i+(limit>>1)]=a1[i]-w*a2[i];//利用单位根的性质，O(1)得到另一部分
}
int main()
{
    int N=read(),M=read();
    for(int i=0;i<=N;i++) a[i].x=read();
    for(int i=0;i<=M;i++) b[i].x=read();
    int limit=1;while(limit<=N+M) limit<<=1;
    fast_fast_tle(limit,a,1);
    fast_fast_tle(limit,b,1);
    //后面的1表示要进行的变换是什么类型
    //1表示从系数变为点值
    //-1表示从点值变为系数
    //至于为什么这样是对的，可以参考一下c向量的推导过程，
    for(int i=0;i<=limit;i++)
        a[i]=a[i]*b[i];
    fast_fast_tle(limit,a,-1);
    for(int i=0;i<=N+M;i++) printf("%d ",(int)(a[i].x/limit+0.5));//按照我们推倒的公式，这里还要除以n
    return 0;
}

这里还有一个听起来很装B的优化—蝴蝶操作

观察合并的过程，w*a2[i] 这一项计算了两次，因为理论上来说复数的乘法是比较慢的，所以我们可以把这一项记出来

此处我犯了一个概念性的错误，蝴蝶操作应当是下面的“迭代实现”。。

    for(int i=0;i<(limit>>1);i++,w=w*Wn)//这里的w相当于公式中的k
    {
        complex t=w*a2[i];//蝴蝶操作
        a[i]=a1[i]+t,
        a[i+(limit>>1)]=a1[i]-t;//利用单位根的性质，O(1)得到另一部分
    }

下面介绍一种更高效的方法

迭代实现

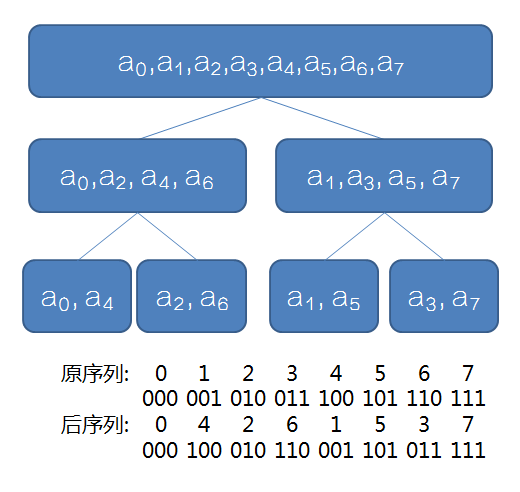
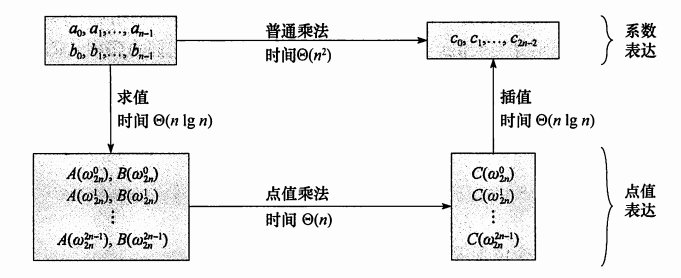
观察一下原序列和反转后的序列？

聪明的你有没有看出什么显而易见的性质？

没错！

我们需要求的序列实际是原序列下标的二进制反转！

因此我们对序列按照下标的奇偶性分类的过程其实是没有必要的

这样我们可以O(n)利用某种操作得到我们要求的序列，然后不断向上合并就好了

// luogu-judger-enable-o2
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
;
inline int read()
{
    ,f=;
    ;c=getchar();}
    +c-';c=getchar();}
    return x*f;
}
const double Pi=acos(-1.0);
struct complex
{
    double x,y;
    complex (,){x=xx,y=yy;}
}a[MAXN],b[MAXN];
complex operator + (complex a,complex b){ return complex(a.x+b.x , a.y+b.y);}
complex operator - (complex a,complex b){ return complex(a.x-b.x , a.y-b.y);}
complex operator * (complex a,complex b){ return complex(a.x*b.x-a.y*b.y , a.x*b.y+a.y*b.x);}//不懂的看复数的运算那部分
int N,M;
int l,r[MAXN];
;
void fast_fast_tle(complex *A,int type)
{
    ;i<limit;i++)
        if(i<r[i]) swap(A[i],A[r[i]]);//求出要迭代的序列
    ;mid<limit;mid<<=)//待合并区间的长度的一半
    {
        complex Wn( cos(Pi/mid) , type*sin(Pi/mid) ); //单位根 , (2*Pi)/(2*m),2*m表示当前整个区间长度.
        ,j=;j<limit;j+=R)//R是区间的长度，j表示当前已经到哪个位置了
        {
            complex w(,);//幂
            ;k<mid;k++,w=w*Wn)//枚举左半部分
            {
                 complex x=A[j+k],y=w*A[j+mid+k];//蝴蝶效应
                A[j+k]=x+y;
                A[j+mid+k]=x-y;
            }
        }
    }
}

#if 1
int main()
{
    int N=read(),M=read();
    ;i<=N;i++) a[i].x=read();
    ;i<=M;i++) b[i].x=read();
    ,l++;
    // 二进制反转
    ;i<limit;i++)
        r[i]= ( r[i>>]>> )| ( (i&)<<(l-) ) ;
    // 在原序列中 i 与 i/2 的关系是 ： i可以看做是i/2的二进制上的每一位左移一位得来
    // 那么在反转后的数组中就需要右移一位，同时特殊处理一下奇数
    fast_fast_tle(a,);//系数化为点值
    fast_fast_tle(b,);//系数化为点值
    ;i<=limit;i++) a[i]=a[i]*b[i]; // 点乘法
    fast_fast_tle(a,-);//点值化为系数
    ;i<=N+M;i++)
        printf("%d ",(int)(a[i].x/limit+0.5)); // 四舍五入，避免误差
    ;
}
#endif

#if 0
// test fft index
#define limit 8
int main()
{
    printf("m, R, j, k, j+k, j+mid+k\n");
    ;mid<limit;mid<<=)//待合并区间的长度的一半
        //complex Wn( cos(Pi/mid) , type*sin(Pi/mid) ); //单位根
        ,j=;j<limit;j+=R)//R是区间的长度，j表示当前已经到哪个位置了
            //complex w(1,0);//幂
            ;k<mid;k++/*,w=w*Wn*/)//枚举左半部分
                printf("%-2d %-2d %-2d %-2d %-2d   %-2d\n", mid, R, j, k, j+k, j+mid+k);
                //complex x=A[j+k],y=w*A[j+mid+k];//蝴蝶效应
//                A[j+k]=x+y;
//                A[j+mid+k]=x-y;
    ;
}
#endif

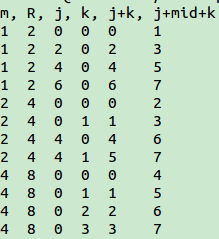
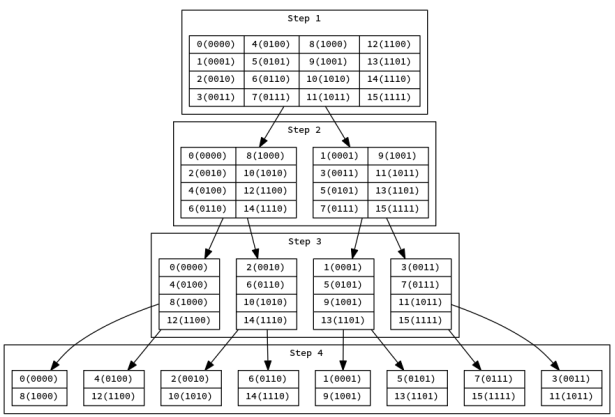
一点点认识: 之所以用迭代,是因为递归方法求解时,重复计算一些值.而通过递归,如上面的15阶多项式,递归时,计算机进行自上而下的堆栈操作

而迭代时自下而上的"用户操作".

ωkn=cos k∗2πn+isink∗2π