【题解】AC自动机题解合集

　　最近貌似大家都在搞字符串？很长一段时间都没有写博客了……还是补一补坑吧。

　　感觉AC自动机真的非常优美了，通过在trie树上建立fail指针可以轻松解决多模匹配的问题。实际上在AC自动机上的匹配可以看做是拿着一个串在上面跑，在固定一个左端点的时候尽量地向右匹配。如果发现实在是匹配不下去了，就向右挪动左端点实现新的匹配（跳转fail指针）。基本上根据这一条理解，就可以解决大部分的问题了。

　　AC自动机裸考的不多，除了匹配之外一个较常见的搭配就是和DP结合在一起。但本质上依然是在匹配串，只要根据fail指针的指向去转移dp状态即可。

　　1.[HNOI2006] 最短母串问题

　　　　非常明确的指向：n <= 12。一眼状压，我们建立状态 \(f[u][S]\) 表示在匹配到AC自动机上的状态 \(u\) 的时候，已经匹配上的串为 \(S\) 集合时的方案数。也许会有疑问：那么怎么保证步数最短&能够输出字典序最小的解？注意AC自动机上相邻状态的转移意味着添加了一个字符，这样我们可以方便地BFS转移。优先转移小的字符可以保证字典序最小，发现答案后直接输出即可。

#include <bits/stdc++.h>
using namespace std;
#define maxn 605
#define maxc 55
#define maxm 5000
int n, tot, cnt, Ans[maxn];
int ch[maxn][], fail[maxn];
int mark[maxn], bits[];
char s[maxc];

struct node
{
    int b;
    short a, c;
    node(short _a = , int _b = , short _c = -)
    { a = _a, b = _b, c = _c; }
}g[maxn][maxm], ans; queue <node> q;

void Ins(int x)
{
    int L = strlen(s + ), p = ;
    for(int i = ; i <= L; i ++)
    {
        int u = s[i] - 'A';
        if(!ch[p][u]) ch[p][u] = ++ tot;
        p = ch[p][u];
    }
    mark[p] = (mark[p] | bits[x - ]);
}

void Build()
{
    queue <int> q;
    for(int i = ; i < ; i ++)
        if(ch[][i]) q.push(ch[][i]);
    while(!q.empty())
    {
        int u = q.front(); q.pop();
        for(int i = ; i < ; i ++)
        {
            if(ch[u][i])
            {
                fail[ch[u][i]] = ch[fail[u]][i];
                mark[ch[u][i]] |= mark[fail[ch[u][i]]];
                q.push(ch[u][i]);
            }
            else ch[u][i] = ch[fail[u]][i];
        }
    }
}

void DP()
{
    q.push(node(, )); g[][].c = -;
    while(!q.empty())
    {
        node now = q.front(); q.pop();
        int u = now.a, S = now.b;
        if(S == bits[n] - ) { ans = node(u, S, g[u][S].c); break; }
        for(int i = ; i < ; i ++)
        {
            int v = ch[u][i], s = S | mark[v];
            if(g[v][s].c == -)
            {
                g[v][s] = node(u, S, i);
                q.push(node(v, s));
            }
        }
    }
}

int main()
{
    scanf("%d", &n);
    bits[] = ; for(int i = ; i < ; i ++) bits[i] = bits[i - ] << ;
    for(int i = ; i <= n; i ++)
    {
        scanf("%s", s + );
        Ins(i);
    }
    Build(); DP();
    for(; g[ans.a][ans.b].c != -; ans = g[ans.a][ans.b])
        Ans[++ cnt] = g[ans.a][ans.b].c;
    for(int i = cnt; i >= ; i --) printf("%c", Ans[i] + 'A');
    return ;
}

　　

　　2.[JSOI2009] 密码

　　emmmm……如果没有输出方案一说，和上题完全就是一样的做法但是我们要输出方案呀？想想如果想要在AC自动机上去爆搜也保证复杂度的话，大概借助一个dp数组表示从当前状态往后转移是否可能出现合法解就好了吧？所以状态的设立定为从当前状态走到目的状态的方案数。记忆化搜索大法好！（但是好像没有人这么写？明明这样写真的又无脑又简单呀……）

#include <bits/stdc++.h>
using namespace std;
#define maxn 100000
#define int long long
int n, m, tot, bits[], f[][][];
int cnt, mark[maxn], fail[maxn], ch[maxn][];
char s[maxn];

int read()
{
    int x = , k = ;
    char c; c = getchar();
    while(c < '' || c > '') { if(c == '-') k = -; c = getchar(); }
    while(c >= '' && c <= '') x = x *  + c - '', c = getchar();
    return x * k;
}

void Ins(int x)
{
    int t = strlen(s + ), p = ;
    for(int i = ; i <= t; i ++)
    {
        int u = s[i] - 'a';
        if(!ch[p][u]) ch[p][u] = ++ tot;
        p = ch[p][u];
    }
    mark[p] |=  bits[x - ];
}

void Build()
{
    queue <int> q;
    for(int i = ; i < ; i ++)
        if(ch[][i]) q.push(ch[][i]);
    while(!q.empty())
    {
        int u = q.front(); q.pop();
        for(int i = ; i < ; i ++)
        {
            int v = ch[u][i];
            if(v)
            {
                fail[v] = ch[fail[u]][i];
                mark[v] |= mark[fail[v]];
                q.push(v);
            }
            else ch[u][i] = ch[fail[u]][i];
        }
    }
}

void Up(int &x, int y) { x = (x + y); }
int DP(int x, int y, int z)
{
    if(z == n && y == bits[m] - ) return f[x][y][z] = ;
    else if(z == n) return ;
    if(f[x][y][z] != -) return f[x][y][z];
    else f[x][y][z] = ;
    for(int c = ; c < ; c ++)
    {
        int v = ch[x][c];
        Up(f[x][y][z], DP(v, y | mark[v], z + ));
    }
    return f[x][y][z];
}

void dfs(int x, int y, int z)
{
    if(z == n)
    {
        for(int i = ; i <= cnt; i ++) printf("%c", s[i]);
        puts(""); return;
    }
    for(int c = ; c < ; c ++)
    {
        int v = ch[x][c];
        if(f[v][y | mark[v]][z + ] > )
        {
            s[++ cnt] = c + 'a';
            dfs(v, y | mark[v], z + );
            cnt --;
        }
    }
}

signed main()
{
    n = read(), m = read();
    memset(f, -, sizeof(f));
    bits[] = ; for(int i = ; i < ; i ++) bits[i] = bits[i - ] << ;
    for(int i = ; i <= m; i ++)
    {
        scanf("%s", s + );
        Ins(i);
    }
    Build(); DP(, , );
    printf("%lld\n", f[][][]);
    if(f[][][] > ) return ;
    dfs(, , );
    return ;
}

　　3.[BJOI2017] 魔法咒语

　　　　这题首先观察一下数据范围，发现一定是两种做法的题（并没有统一的数据范围）。前面的直接暴力建立状态 \(f[i][j]\) 表示第 \(i\) 个字符匹配到了AC自动机上的 \(j\) 状态的方案数。可以枚举用哪一个串转移，只要不会踩到禁忌状态就可以转移。为了降低复杂度，可以预处理一下。至于后面的数据，看到这么大的数据范围显然矩阵。发现长度 <= 2；所以我们可以有：

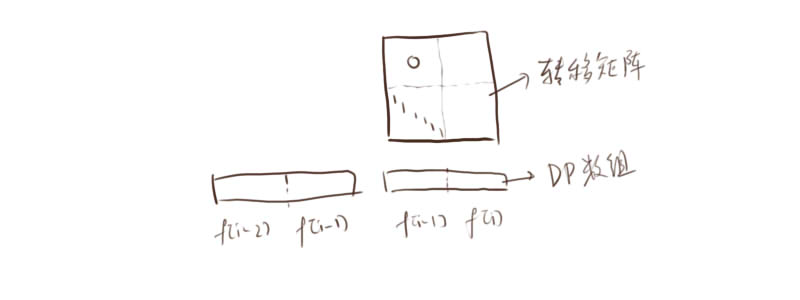
　　差不多这样子去构造矩阵。状态和转移方式是不变的，构造矩阵优化dp就好。

#include <bits/stdc++.h>
using namespace std;
#define maxn 6300
#define maxm 205
#define mod 1000000007
int n, m1, m2, ans, tot, f[maxm][maxn];
int len[maxn], ch[maxn][], fail[maxn];
int rec1[maxn][maxn], rec2[maxn][maxn], trans[maxn][maxm];
bool error[maxn];
char s[maxm][maxm];

struct matrix
{
    int a[][];
    matrix() { memset(a, , sizeof(a)); }
    friend matrix operator *(const matrix& a, const matrix& b)
    {
        matrix c;
        memset(c.a, , sizeof(c.a));
        int t = tot * ;
        for(int i = ; i <= t; i ++)
            for(int j = ; j <= t; j ++)
                for(int k = ; k <= t; k ++)
                    c.a[i][j] = (c.a[i][j] + 1ll * a.a[i][k] * b.a[k][j] % mod) % mod;
        return c;
    }
}M;

void Up(int &x, int y) { x = (x + y); if(x >= mod) x -= mod; }
void Ins(int x)
{
    int p = ; len[x] = strlen(s[x] + );
    for(int i = ; i <= len[x]; i ++)
    {
        int v = s[x][i] - 'a';
        if(!ch[p][v]) ch[p][v] = ++ tot;
        p = ch[p][v];
    }
    error[p] = ;
}

int Get(int u, int x)
{
    int p = u;
    for(int i = ; i <= len[x]; i ++)
    {
        int v = s[x][i] - 'a';
        if(error[p]) return -;
        p = ch[p][v];
    }
    if(error[p]) return -;
    return p;
}

void Build()
{
    queue <int> q;
    for(int i = ; i < ; i ++) if(ch[][i]) q.push(ch[][i]);
    while(!q.empty())
    {
        int u = q.front(); q.pop();
        for(int i = ; i < ; i ++)
        {
            int v = ch[u][i];
            if(v)
            {
                fail[v] = ch[fail[u]][i];
                error[v] |= error[fail[v]];
                q.push(v);
            }
            else ch[u][i] = ch[fail[u]][i];
        }
    }
    for(int j = ; j <= tot; j ++)
        for(int i = ; i <= m1; i ++)
        {
            trans[j][i] = Get(j, i); if(trans[j][i] == -) continue;
            if(len[i] == ) rec1[j + ][trans[j][i] + ] ++;
            else rec2[j + ][trans[j][i] + ] ++;
        }
}

void DP1()
{
    f[][] = ;
    for(int k = ; k <= n; k ++)
        for(int i = ; i <= tot; i ++)
        {
            if(!f[k][i]) continue;
            for(int j = ; j <= m1; j ++)
            {
                int t = trans[i][j];
                if(t == -) continue;
                else if(k + len[j] <= n) Up(f[k + len[j]][t], f[k][i]);
            }
        }
    for(int i = ; i <= tot; i ++)
        if(!error[i]) Up(ans, f[n][i]);
}

matrix Qpow(int timer)
{
    matrix base;
    memset(base.a, , sizeof(base.a));
    for(int i = ; i <=  * tot; i ++) base.a[i][i] = ;
    for(; timer; timer >>= , M = M * M)
        if(timer & ) base = base * M;
    return base;
}

void DP2()
{
    tot ++; int t =  * tot;
    for(int i = tot + ; i <= t; i ++) M.a[i][i - tot] = ;
    for(int i = ; i <= tot; i ++)
        for(int j = tot + ; j <= t; j ++)
            M.a[i][j] = rec2[i][j - tot];
    for(int i = tot + ; i <= t; i ++)
        for(int j = tot + ; j <= t; j ++)
            M.a[i][j] = rec1[i - tot][j - tot];

    matrix ret = Qpow(n), S;
    memset(S.a, , sizeof(S.a)); S.a[][tot + ] = ;
    S = S * ret;
    for(int i = tot + ; i <= t; i ++)
        if(!error[i - tot - ]) Up(ans, S.a[][i]);
}

signed main()
{
    scanf("%d%d%d", &m1, &m2, &n);
    for(int i = ; i <= m1; i ++) scanf("%s", s[i] + ), len[i] = strlen(s[i] + );
    for(int i = ; i <= m2; i ++) scanf("%s", s[m1 + ] + ), Ins(m1 + );
    Build();
    if(n <= ) DP1(); else DP2();
    printf("%d\n", ans);
    return ;
}