三：背包DP

01背包问题描述

已知:有一个容量为V的背包和N件物品，第i件物品的重量是weight[i]，收益是cost[i]。

限制:每种物品只有一件，可以选择放或者不放

问题:在不超过背包容量的情况下，最多能获得多少价值或收益

相似问题:在恰好装满背包的情况下，最多能获得多少价值或收益

这里，我们先讨论在不超过背包容量的情况下，最多能获得多少价值或收益。

基本思路

01背包的特点:每种物品只有一件，可以选择放或者不放

子问题定义状态

dp[i][v]:前i件物品放到一个容量为v的背包中可以获得最大价值

状态转移方程

dp[i][v]=max(dp[i-1][v],dp[i-1][v-[weight[i]]+vaule[i]);

分析

考虑我们的子问题，将前i件物品放到容量为v的背包中，若我们只考虑第i件物品时，它有两种选择，放或者不放。

1) 如果第i件物品不放入背包中，那么问题就转换为：将前i - 1件物品放到容量为v的背包中，带来的收益dp[i - 1][v]

2) 如果第i件物品能放入背包中，那么问题就转换为：将前i - 1件物品放到容量为v - weight[i]的背包中，带来的收益dp[i - 1][v - weight[i]] + value[i]

code:

#include <iostream>
#include <cstring>
using namespace std;

][],n,v;
typedef struct
{
    int weight,value;
}K;
K k[];

int knaspack()
{
    ;i<=n;++i)
    {
        ;j<=v;++j)
        {
            dp[i][j]=dp[i-][j];
            if(j>=k[i].weight)
                dp[i][j]=max(dp[i-][j],dp[i-][j-k[i].weight]+k[i].value);
        }
    }
    return dp[n][v];
}

int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        memset(dp,,sizeof(dp));
        cin>>n>>v;
        ;i<n;++i)
            cin>>k[i].weight>>k[i].value;

        cout<<knaspack()<<endl;
    }
    ;
}

效率分析：

此算法的时间复杂度为O(N*V)，空间复杂度也为O(N*V)。其中，N 表示物品个数，V 表示背包容量这里，时间复杂度不可以在优化了，但是空间复杂度可以继续优化到O(V)

优化空间复杂度

上述的方法，我们使用二维数组 f[i][v] 保存中间状态，这里我们可以使用一维数组f[v]保存中间状态就能得到结果

分析

我们现在使用f[v]保存中间状态，我们想要达到的效果是，第i次循环后，f[v]中存储的是前i个物体放到容量v时的最大价值

在回顾下之前讲过的状态转移方程：

dp[i][v]=max(dp[i-1][v],dp[i-1][v-[weight[i]]+vaule[i]);

我们可以看到，要想得到 f[i][v]，我们需要知道 f[i - 1][v] 和 f[i - 1][v - weight[i]]，由于我们使用二维数组保存中间状态，所以可以直接取出这两个状态。

当我们使用一维数组存储状态时，f[v]表示，在执行i次循环后(此时已经处理i个物品)，前i个物体放到容量v时的最大价值，即之前的f[i][v]。与二维相比较，它把第一维隐去了，但是二者表达的含义还是相同的，只不过针对不同的i，f[v]一直在重复使用，所以，也会出现第i次循环可能会覆盖第i - 1次循环的结果。

为了求f[v],我们需要知道，前i - 1个物品放到容量v的背包中带来的收益，即之前的f[i - 1][v]  和 前i - 1件物品放到容量为v - weight[i]的背包中带来的收益，即之前的f[i - 1][v - weight[i]] + cost[i]。

难点：由于我们只使用一维数组存储，则在求这两个子问题时就没有直接取出那么方便了，因为，第i次循环可能会覆盖第i - 1次循环的结果。

现在我们来求这两个值

1）前i - 1个物品放到容量v的背包中带来的收益，即之前的f[i - 1][v] ：

由于，在执行在i次循环时，f[v]存储的是前i个物体放到容量v时的最大价值，在求前i个物体放到容量v时的最大价值(即之前的f[i][v])时，我们是正在执行第 i 次循环，f[ v ]的值还是在第 i - 1  次循环时存下的值，在此时取出的 f[ v ]就是前i - 1个物体放到容量v时的最大价值，即f[i - 1][v]。

2）前i - 1件物品放到容量为v - weight[i]的背包中带来的收益，即之前的f[i - 1][v - weight[i]] + cost[i]

由于，在执行第i次循环前，f[0 ~ V]中保存的是第i - 1次循环的结果，即是前i - 1个物体分别放到容量0 ~ V时的最大价值，即f[i - 1][0 ~ V]。

则，在执行第i次循环前，f 数组中v - weight[i]的位置存储就是我们要找的 前i - 1件物品放到容量为v - weight[i]的背包中带来的收益 (即之前的f[i - 1][v - weight[i]])，这里假设物品是从数组下标1开始存储的。

伪代码

..N //枚举物品
     //枚举容量，从大到小
        dp[v]=max{dp[v],dp[v-weight[i]] + cost[i]};

由上面伪代码可知，在执行第 i 次循环时，需要把背包容量由V..0都要遍历一遍，检测第 i 件物品是否能放。

逆序枚举容量的原因：

注意一点，我们是由第 i - 1 次循环的两个状态推出 第 i 个状态的，而且 v  > v - weight[i]，则对于第i次循环，背包容量只有当V..0循环时，才会先处理背包容量为v的状况，后处理背包容量为 v-weight[i] 的情况。

具体来说，由于，在执行v时，还没执行到v - weight[i]的，因此，f[v - weight[i]]保存的还是第i - 1次循环的结果。即在执行第i次循环 且 背包容量为v时，此时的f[v]存储的是 f[i - 1][v] ，此时f[v-weight[i]]存储的是f[i - 1][v-weight[i]]。

相反，如果在执行第 i 次循环时，背包容量按照0..V的顺序遍历一遍，来检测第 i 件物品是否能放。此时在执行第i次循环 且 背包容量为v时，此时的f[v]存储的是 f[i - 1][v] ，但是，此时f[v-weight[i]]存储的是f[i][v-weight[i]]。

因为，v  > v - weight[i]，第i次循环中，执行背包容量为v时，容量为v - weight[i]的背包已经计算过，即f[v - weight[i]]中存储的是f[i][v - weight[i]]。即，对于01背包，按照增序枚举背包容量是不对的。

code

#include <iostream>
#include <cstring>
using namespace std;

],n,v;
typedef struct
{
    int weight,value;
}K;
K k[];

int kanpsack()
{
    ;i<=n;++i)
    {
        for(int j=v;j>=k[i].weight;--j)
            dp[j]=max(dp[j],dp[j-k[i].weight]+k[i].value);
    }
    return dp[v];
}

int main()
{
    int t;
    cin>>t;//测试数据的组数
    while(t--)
    {
        memset(dp,,sizeof(dp));
        cin>>n>>v;//n为物品的种类数，v为背包最大的容量 

        ;i<=n;++i)
            cin>>k[i].weight>>k[i].value;

        cout<<kanpsack()<<endl;
    }
    ;
}

1. 子问题状态:f[j]:表示前i件物品放入容量为j的背包得到的最大价值
2. 初始化:f数组全设置为0

但是，增序枚举背包容量会达到什么效果：它会重复的装入某个物品，而且尽可能多的，使价值最大，当然不会不超过背包容量

而逆序枚举背包容量：背包中的物品至多装一次，使价值最大，当然不会不超过背包容量

我们首先举例说明：

逆序枚举物品

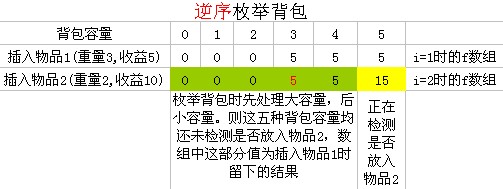
当i = 2，我们要求 f [5]：表示检测物品2放入容量为5的背包的最大收益

上图表示，当i = 2，求f[5]时f数组的状况，

橙色为数组现在存储的值，这些值是i = 1时(上一次循环)存入数组 f 的。相当于f[i - 1][v]

而黄色使我们要求的值，在求f[5]之前，f[5]= 5，即f[i - 1][5] = 5

现在要求 i = 2 时的f[5] = f[5 - 2] + 10 = 5 + 10 = 15  >  f[i - 1][5] = 5

故，f[5] = 15；

注意一点，在求f[v]时，它引用的 f[v - weight[i]] 和 f[v]都是上一次循环的结果

顺序枚举物品

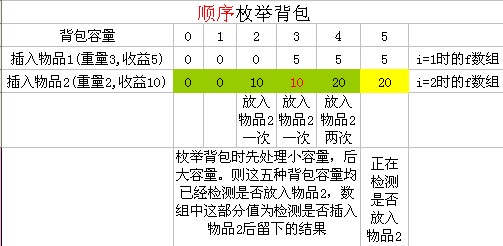
当i = 2，我们要求 f [5]：表示检测物品2放入容量为5的背包的最大收益

上图表示，当i = 2，求f[5]时f数组的状况，

橙色为数组现在存储的值，这些值是i = 2时(本次循环)存入数组 f 的。相当于f[i][v]

这是由于，我们是增序遍历数组f的，在求f[v]时，v之前的值(0 ~ v - 1)都已经在第i次循环中求出。

而黄色使我们要求的值，在求f[5]之前，f[5]= 5，即f[i - 1][5] = 5

现在要求 i = 2 时的f[5] = f[5 - 2] + 10 =10+ 10 = 20 >  f[i - 1][5] = 5

故，f[5] = 20；

其中引用的f[3]是相当于f[i][3] 而不是正常的f[i - 1][3]

注意一点，在求f[v]时，它引用的 f[v - weight[i]]是本次循环的结果 而f[v]是上一次循环的结果

换个角度说，

在检测 背包容量为5时，看物品2是否加入

由状态转移方程可知，我们f[5]需要引用自己本身和f[3]

由于背包容量为3时，可以装入物品2，且收益比之前的大，所以放入背包了。

在检测f[5]时，肯定要加上物品2的收益，而f[5]在引用f[3]时，f[3]时已经加过一次物品2，

因此，在枚举背包容量时，物品2会加入多次。

进一步说：

我们观察一维状态转移方程：

f[i][v] = max(f[i - 1][v],f[i - 1][v - weight[i]] + cost[i])

首先我们明确三个问题

1) v - weight[i] < v

2) 状态f[i][v] 是由 f[i - 1][v] 和 f[i - 1][v - weight[i]] 两个状态决定

3) 对于物品i，我们在枚举背包容量时，只要背包容量能装下物品i 且 收益比原来的大，就会成功放入物品i。

具体来说，枚举背包容量时，是以递增的顺序的话，由于 v - weight[i] < v,则会先计算 v - weight[i]。在背包容量为v - weight[i]时，一旦装入了物品i，由于求f[v]需要使用f[i - 1][v - weight[i]]，而若求f[v]时也可以装入物品i的话，那么在背包容量为v时，容量为v的背包就装入可两次物品。又若v - weight[i]是由之前的状态推出，它们也成功装入物品i的话，那么容量为v的背包就装入了多次物品i了。

注意，此时，在计算f[v]时，已经把物品i能装入的全装入容量为v的背包了，此时装入物品i的次数为最大啊

其实，顺序枚举容量是完全背包问题最简捷的解决方案。

初始化的细节问题

求最优解的背包问题时，有两种问法：

1)在不超过背包容量的情况下，最多能获得多少价值

2)在恰好装满背包的情况下，最多能获得多少价值

主要的区别为是否要求恰好装满背包。但这两种问法的实现方法是在初始化的时候有所不同。

1)恰好装满背包的情况：使用二维数组f[i][v]存储中间状态，其中第一维表示物品，第二维表示背包容量

初始化时，除了f[i][0] = 0（第一列）外，其他全为负无穷。

原因：初始化 f 数组就是表示：在没有任何物品可以放入背包时的合法状态。对于恰好装满背包，只有背包容量为 0（第一列），可以什么物品都不装就能装满，这种情况是合法情况，此时价值为0。其他f[0][v]（第一列）是都不能装满的，此时有容量没物品。而其他位置（除去第一行和第一列的位置），我们为了在计算中比较最大值，也要初始化为负无穷。我们从程序的角度上看，我们只允许装入背包物品的序列的起始位置是从第一列开始，这些起始位置都是合法位置，且能恰好装满的情况收益均为正值，到f[N][V]终止。

注意，我们虽然是求恰好装满，还是需要枚举所有可以装入背包的物品，只要能装入，还需装入，收益有增加。只不过，由于恰好装满的物品的序列肯定是从第一列某行开始的，且之后的收益肯定是正值。对于非恰好装满的物品序列，其实位置肯定是从第一行某位置开始的，由于此时被初始化为负无穷，在和那些恰好装满物品序列带来的价值时，肯定是小的。所以，我们最后能获得最大值。

代码：

（今天先到这明天再跟新...）