python 实现插入排序、冒泡排序、归并排序

 def InsertSort(A):
 	'''插入排序算法：传入一个list，对list中的数字进行排序'''
 	print('插入排序前list元素顺序：',A)
 	length=len(A)
 	for i  in range(1,length):#从第二个开始
 		key=A[i]
 		j=i-1
 		while j>=0 and A[j]>key:
 			A[j+1]=A[j]
 			j=j-1
 		A[j+1]=key
 	print('插入排序后的list元素顺序：',A)
 	#插入排序时间复杂度:n^2,空间复杂度:1,相同元素保持相对不变性(相对位置不变)

 def BableSort(A):
     '''冒泡排序算法：传入一个List，对list中的元素进行排序'''
     print('冒泡排序前的顺序：',A)
     length=len(A)
     for i in range(1,length):
         #rang=range(i)
         #for j in reversed(rang):
         for j in range(i,0,-1): #range逆序遍历
             if A[j-1]> A[j]:
                 temp=A[j]
                 A[j]=A[j-1]
                 A[j-1]=temp

     print('冒泡排序后的顺序：',A)
     # 冒泡排序时间复杂度为：n^2,空间复杂度1，相同元素保持相对不变性

 # 归并排序，传入一个list，对list元素进行排序
 def MergeSort(alist):
     print("Splitting ",alist)
     if len(alist)>1:
         mid = len(alist)//2#精确除法，取小于等于结果的最大整数，相当于对结果进行向下取整
         lefthalf = alist[:mid]
         righthalf = alist[mid:]

         MergeSort(lefthalf)#递归调用左半部分
         MergeSort(righthalf)#递归调用右半部分

         #合并过程
         i=0
         j=0
         k=0
         while i < len(lefthalf) and j < len(righthalf):
             if lefthalf[i] < righthalf[j]:
                 alist[k]=lefthalf[i]
                 i=i+1
             else:
                 alist[k]=righthalf[j]
                 j=j+1
             k=k+1

         while i < len(lefthalf):
             alist[k]=lefthalf[i]
             i=i+1
             k=k+1

         while j < len(righthalf):
             alist[k]=righthalf[j]
             j=j+1
             k=k+1
     print("Merging ",alist)
     # 归并排序算法时间复杂度：n*lgn,空间复杂度:n,相同元素保持顺序不变性

 if __name__=='__main__':
     listA=[1,5,7,3,4,6,7,8,9,9,15,10,4]
     alist = [54,26,93,17,77,31,44,55,20]
     #InsertSort(listA)
     #BableSort(listA)
     MergeSort(alist)

      

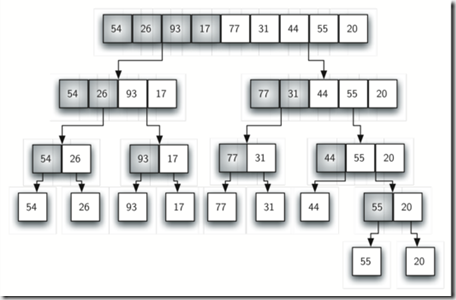
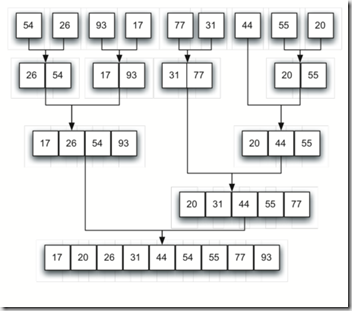
参考：http://interactivepython.org/courselib/static/pythonds/SortSearch/TheMergeSort.html