NEFU 117 - 素数个数的位数 - [简单数学题]

题目链接：http://acm.nefu.edu.cn/JudgeOnline/problemShow.php?problem_id=117

Time Limit:1000ms　　Memory Limit:65536K

Description

小明是一个聪明的孩子，对数论有着很浓烈的兴趣。他发现求1到正整数10n 之间有多少个素数是一个很难的问题，该问题的难以决定于n 值的大小。现在的问题是，告诉你n的值，让你帮助小明计算小于10n的素数的个数值共有多少位？

Input

输入数据有若干组，每组数据包含1个整数n（1 < n < 1000000000），若遇到EOF则处理结束。

Output

对应每组数据，将小于10n 的素数的个数值的位数在一行内输出，格式见样本输出。同组数据的输出，其每个尾数之间空一格，行末没有空格。

Sample Input

3
7

Sample Output

3
6

题解：

这道题目可以说是比较有趣的数学题，相比于算法，考得更多的应该是数学上的内容吧。

因为不可能真的去遍历1到10^n一个一个判断是否为素数，然后求出个数，在求位数，显然TLE，所以换其他思路；

首先，根据素数定理，可知π(x) ≈ n / ln(n)，向本题中，问的是位数，那用约等于问题就不大，两者相差没到10倍就可以说位数上是一样的；

故根据题意，就有：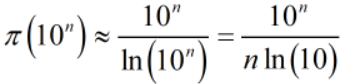

那么，如何求这个数的位数呢，也很简单用log(10,x)+1即可：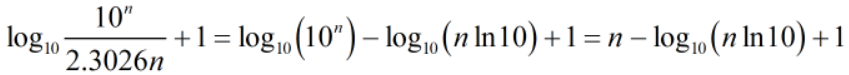

AC代码：

 #include<cstdio>
 #include<cmath>
 int n;
 int main()
 {
     while(scanf("%d",&n)!=EOF)
     {
         double ans=n-log10(n*log())+;
         printf("%d\n",int(ans));
     }
 }