PCA和SVD(转)

最近突然看到一个问题，PCA和SVD有什么关系？隐约记得自己照猫画虎实现的时候PCA的时候明明用到了SVD啊，但SVD（奇异值分解）和PCA的（特征值分解）貌似差得相当远，由此钻下去搜集了一些资料，把我的一些收获总结一下，以免以后再忘记。

PCA的简单推导

PCA有两种通俗易懂的解释，

1)是最大化投影后数据的方差(让数据更分散)；地址：http://www.cnblogs.com/shixisheng/p/7107363.html

2)是最小化投影造成的损失。（下边讲的就是这个方法）

这两个思路最后都能推导出同样的结果。 
下图应该是对PCA第二种解释展示得最好的一张图片了(ref:svd,pca,relation) 

def pca_01(X):
    covMat = np.cov(X,rowvar = 0)
    eigVal,eigVec = sp.linalg.eig(covMat)
    #do reduction with eigVal,eigVec

但因为最后用于变换的矩阵需要是去中心化后的，所以有些地方的实现是：

def pca_02(X):
    mean_ = np.mean(X, axis=0)
    X = X - mean_
    covMat = np.cov(X,rowvar = 0)#实际上是否去中心化对求到的协方差矩阵并无影响,只是方便后面进行降维
    eigVal,eigVec = sp.linalg.eig(covMat)
    #do reduction with eigVal,eigVec

使用矩阵乘法的方式：

def pca_03(X):
    mean_ = np.mean(X, axis=0)
    X = X - mean_
    M,N=X.shape
    Sigma=np.dot(X.transpose(),X)/(M-1)
    eigVal,eigVec = sp.linalg.eig(Sigma)
    #do reduction with eigVal,eigVec

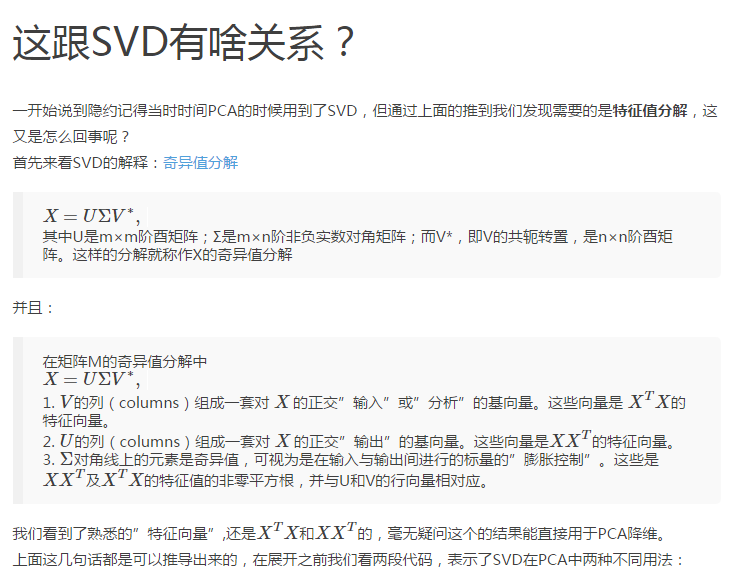
酉矩阵：n阶复方阵U的n个列向量是U空间的一个标准正交基，则U是酉矩阵(Unitary Matrix)。显然酉矩阵是正交矩阵往复数域上的推广。

def pca_04(X):
    mean_ = np.mean(X, axis=0)
    X = X - mean_
    M,N=X.shape
    Sigma=np.dot(X.transpose(),X) #这里直接去掉/(M-1)方便和pca_05比较，对求得特征向量无影响
    U,S,V = sp.linalg.svd(Sigma);
    eigVal,eigVec = S,U
    #do reduction with eigVal,eigVec

可以看到在pca_03的基础上我们把sp.linalg.eig改用了sp.linalg.svd，这涉及到： 
结论1：协方差矩阵（或X^TX）的奇异值分解结果和特征值分解结果一致。

def pca_05(X):
    mean_ = np.mean(X, axis=0)
    X = X - mean_
    U, S, V = sp.linalg.svd(X)
    eigVal,eigVec = S,V
    #do reduction with eigVal,eigVec

PCA_04:
eigVal：[ 21.60311815 8.77188185]
eigVec： [[-0.88734696 -0.46110235]
[-0.46110235 0.88734696]]

PCA_05:
eigVal：[ 4.64791546 2.96173629]
eigVec： [[ 0.88734696 0.46110235]
[-0.46110235 0.88734696]]
#注意PCA_05结果中特征向量维度的符号，和上面不太一样，但这不影响降维的功能，每一列是一组基

转自：http://blog.csdn.net/dark_scope/article/details/53150883