动态规划-Largest Sum of Averages

2018-07-12 23:21:53

问题描述：

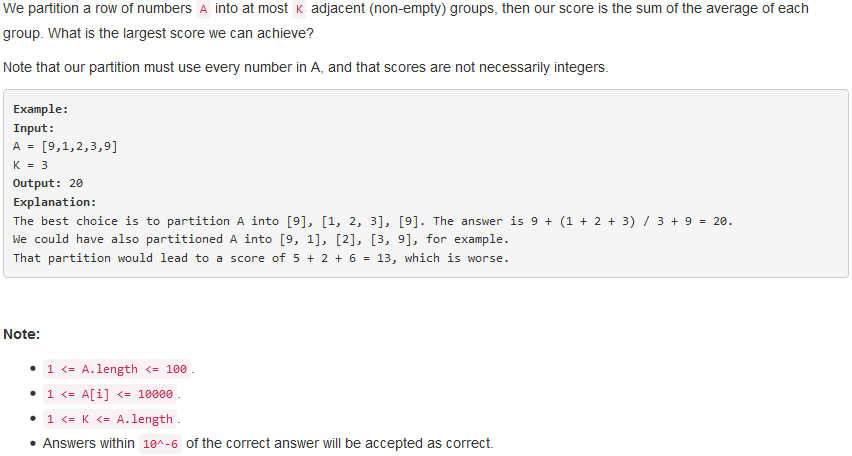
问题求解：

dp[i][j] : 以ai结尾的分j个部分得到的最大值

dp[i][j] = max{dp[k][j - 1] + (a_k+1 + ... + a_i) / (i - k)} k = [j - 2, i - 1]

    public double largestSumOfAverages(int[] A, int K) {
        double[][] dp = new double[A.length][K + 1];
        int curSum = 0;
        for (int i = 0; i < A.length; i++) {
            curSum += A[i];
            dp[i][1] = curSum * 1.0 / (i + 1);
        }
        for (int k = 2; k <= K; k++) {
            for (int i = k - 1; i < A.length; i++) {
                for (int j = k - 2; j < i; j++) {
                    curSum = 0;
                    int idx = j + 1;
                    while (idx <= i) curSum += A[idx++];
                    dp[i][k] = Math.max(dp[i][k], dp[j][k - 1] + curSum * 1.0 / (i - j));
                }
            }
        }
        return dp[A.length - 1][K];
    }