C++中数据对齐问题。struct、union、enum，类继承。再谈sizeof()

首先是struct,在C++中，结构体其实和class有很大的相似了。但是有一点不同的是，struct默认是public，而class中是private.

当然，struct继承等用法也是可以的。

共用体的声明方式是：

枚举的声明方式与共用体比较相似

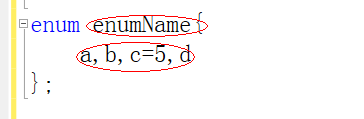
其中a初始化为0,后面默认增1,若已经初始化，则后面再增1，比如d=6在这里。

struct长度计算

大家猜一下，s1 x;int b=sizeof(x);

他的结果会是多少呢？有人会觉得应该是1+8+4+1=14.

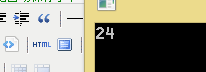
实际上是24.为什么会是这样呢？这个和结构体的对齐方式有很大关系。总之有两条

1、整体空间是最大成员占用字节的整数倍，比如这里最大字节占用的是double,他为8，那肯定是8,16,24...

2、内存按照结构体中的数据成员先后排序，并且当前地址应该是以当前成员所占用空间的整数倍。比如在这里double b占用的是8个字节，那么以摆字节就应该是8,16,24.而char a，只有一个字节，则前面空间自动补齐。

按照上面两点的规则，我们不难得出8+8+4+1,但是应该是8的整数倍，所以是24.

这里有必要补充一下：在Linux+gcc环境下，若最大成员是4，则整体空间只需是4的倍数即可。所以这里只需要是4的倍数，4,8,12,16,20,24..
第二点，在Linux+gcc环境下，若某成员类型所占字节数超过4，那前面已摆放空间只需要是4的倍数即可。这里double b;前面只需补齐4个即可，而不需补齐8个。
故会出现整体空间是20的情况。4+8+4+1=17.但是应该是4的倍数，则为20.

 那么联合体应该是怎么样的呢？

很显然联合体取值的时候只能取其中的一个，那么，联合体就是多个成员公用一个内存空间。大家很自然的就想到了，最大那个成员所占用的空间就是联合体的空间了。

讲到了数据的对齐方式，那我们就非常有必要讲一下两种不同机器的存储方式：大端存储模式和小端存储模式。

大端存储模式：高位字节存储低地位内存中，低位字节存储高位。这里均以0x12345678为例。

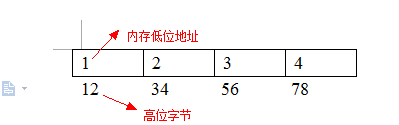
小端存储模式：低位存储在高位内存中

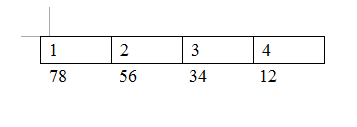
在小端系统中，b的ASCII为多少？

 union enumName {
     int i;
     unsigned char ch[];
 };
 int _tmain(int argc, _TCHAR* argv[])
 {
     enumName student;
        student.i=0x1420;
     char b=student.ch[];
 }

答案应该是32

小端是低位放低位，高位放高位。则是20   14这样排放。ch[0]等于0x20.

其实我们平常使用的计算机很多都是小端存储。

 Update

本来以为数据对齐的问题已经讲完，但是今天看到了一道笔试题，觉得非常有必要再说一下关于类中，继承类的数据成员对齐问题。

  class A{
  public:
      int a;
      char b;
   };
  class B:public A{
  public:
      char c;
  };

我们想一下，sizeof(B)是多少呢?肯定有人觉得他应该是9或者1.

但是其实答案是12.

为什么是12呢？这里我们就要注意到类的对齐方式了。

显然B继承自A，那么B应该包括了A的数据成员，那么对于A来说大小应该是8，这个和结构体的计算方式是一致的。

特别注意第二点，子类的对齐还要考虑父类的情况，在这里表现的就是，A中最大为4，那么最后的数据大小应该是4的整数倍，4,8,12,。

这里本来应该是8+1.但需要自动补齐，因此是12.

转载请注明出处：http://www.cnblogs.com/xiaoyi115/p/3622135.html