BZOJ 1974 [Sdoi2010] auction 代码拍卖会（数位dp）

题目描述

随着iPig在P++语言上的造诣日益提升，他形成了自己一套完整的代码库。猪王国想参加POI的童鞋们都争先恐后问iPig索要代码库。iPig不想把代码库给所有想要的小猪，只想给其中的一部分既关系好又肯出钱的小猪，于是他决定举行了一个超大型拍卖会。

在拍卖会上，所有的N头小猪将会按照和iPig的好感度从低到高，从左到右地在iPig面前站成一排。每个小猪身上都有9猪币（与人民币汇率不明），从最左边开始，每个小猪依次举起一块牌子，上面写上想付出的买代码库的猪币数量（1到9之间的一个整数）。大家都知道，如果自己付的钱比左边的猪少，肯定得不到梦寐以求的代码库，因此从第二只起，每只猪出的钱都大于等于左边猪出的价钱。最终出的钱最多的小猪（们）会得到iPig的代码库真传，向着保送PKU（Pig Kingdom University）的梦想前进。

iPig对自己想到的这个点子感到十分满意，在去现场的路上，iPig就在想象拍卖会上会出现的场景，例如一共会出现多少种出价情况之类的问题，但这些问题都太简单了，iPig早已不敢兴趣了，他想要去研究更加困难的问题。iPig发现如果他从台上往下看，所有小猪举的牌子从左到右将会正好构成一个N位的整数，他现在想要挑战的问题是所有可能构成的整数中能正好被P整除的有多少个。由于答案过大，他只想要知道答案mod 999911659就行了。

输入输出格式

输入格式：

输入文件auction.in有且仅有一行：两个数N（1≤N≤10^18）、P(1≤P≤500)，用一个空格分开。

输出格式：

输入文件auction.out有且仅有一行：一个数，表示答案除以999911659的余数。

输入输出样例

输入样例#1：复制

2 3

输出样例#1：复制

说明

样例解释

方案可以是：12 15 18 24 27 33 36 39 45 48 57 66 69 78 99，共15种。

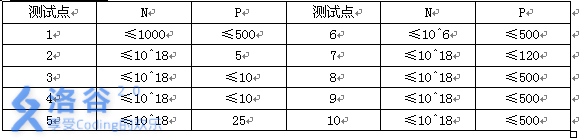
数据规模

题解

　　这题太神仙了……题解看都看不懂……最后基本只能硬生生的理解了……

　　首先，我们考虑数列，原数列是一个不降的序列

　　考虑如下数列，$1,1,2,3,4$

　　这样我们是相当于竖着分割的

　　那么怎么转换为横着分割呢？我们可以记录大于等于$1$的数的个数，为$5$，大于等于$2$的数的个数，为$3$……

　　那么最后原数列可以转化为$11111,111,11,1$（每个数用相同个数的$1$表示），然后我们惊奇的发现他们的和和原来的$n$位数是一样的，也就是说，他们构成的整数取模之后也是一样的！

　　这就相当于在每一个位置放相当于权值大小的石头，我们一开始是竖着分，而第二种方法是横着分割

　　如果竖着分割，总共有$n$个数，如果横着割，把所有模$p$同余的看成一类，那么总共只有$p$个数（因为0,1,11,111这样下去模$p$的值肯定能构成一个循环节，所以只需要计算$p$次，剩下的可以直接计算）

　　那么我们为什么不转化为横着分割呢？设$cnt[i]$表示模$p$为$i$的数的个数，那么题目就变成从$cnt[i]$中取$9$个使下标之和被$p$整除

　　那么就可以转化为dp了，设$f[i][j][k]$表示考虑到第$i$个数，选了$k$个，他们的和模$p$为$j$，那么状态转移方程就是$f[i+1][(j+l*i)%mod][k+l]=(f[i][j][k]*C_{cnt_i}^l+f[i+1][(j+l*i)%mod][k+l])%mod$

　　然后要先考虑加上一个$11111$（$n$个$1$），因为我们dp的时候是允许有前导$0$的，所以得先强制至少为$1$才行

　　细节有点多，都写在注解里了

 //minamoto

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #define ll long long

 using namespace std;

 const int mod=;

 ll ans,n,p,cnt[],beg,len,pos[],A[],c[][],f[][][],a;

 int main(){

     scanf("%lld%d",&n,&p);

     ll sum=;

     if(n<=p){

         //直接把循环节跑出来

         for(int i=;i<=n;++i) sum=(sum*+)%p,++cnt[sum];

         a=sum;

     }else{

         //否则去找循环节，数出每一个余数的出现次数

         for(int i=;i<=p+;++i){

             sum=(sum*+)%p;

             if(cnt[sum]){

                 beg=pos[sum],len=i-pos[sum];

                 break;

             }

             ++cnt[sum],pos[sum]=i;

         }

         for(int i=;i<p;++i)

         if(cnt[i]&&pos[i]>=beg){

             cnt[i]=(n-beg+)/len;

             if(pos[i]-beg+<=(n-beg+)%len) ++cnt[i];

             if((pos[i]-beg+)%len==(n-beg+)%len) a=i;

         }

     }

     A[]=,A[]=;

     for(int i=;i<=;++i)

     A[i]=(mod-mod/i)*A[mod%i]%mod;

     for(int i=;i<p;++i){

         c[i][]=;

         if(cnt[i])

         for(int j=;j<=;++j){

             c[i][j]=cnt[i]*c[i][j-]%mod*A[j]%mod;

             cnt[i]=(cnt[i]+)%mod;

             //C(n,m-1)->C(n,m)

             //C(n,m-1)/m*(n-m+1)=C(n,m)

             //cnt[i]=n-m+1

         }

     }

     f[][a][]=;

     //默认加n个1，因为dp的时候可以有前缀0

     for(int i=;i<p;++i)

     for(int j=;j<p;++j)

     for(int k=;k<;++k)

     for(int l=;l<=k;++l)

     (f[i+][j][k]+=f[i][(j-(l*i%p)+p)%p][k-l]*c[i][l]%mod)%mod;

     for(int i=;i<=;++i) (ans+=f[p][][i])%=mod;

     printf("%lld\n",ans);

     return ;

 }