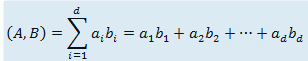BZOJ 3243 向量内积

Description

两个\(d\)维向量\(A=[a_{1},a_{2},...,a_{d}]\)与\(B=[b_{1},b_{2},...,b_{d}]\)的内积为其相对应维度的权值的乘积和，即：



现有\(n\)个\(d\)维向量\(x_{1},...,x_{n}\)，小喵喵想知道是否存在两个向量的内积为\(k\)的倍数。请帮助她解决这个问题

Input

第一行包含\(3\)个正整数\(n,d,k\)，分别表示向量的个数，维数以及待检测的倍数。

接下来\(n\)行每行有\(d\)个非负整数，其中第\(i\)行的第\(j\)个整数表示向量\(x_{i}\)的第\(j\)维权值\(x_{i,j}\)。

Output

包含两个整数，用空格隔开。

如果存在两个向量\(x_{p},x_{q}\)的内积为\(k\)的整数倍，则输出两个向量的编号\(p\)与\(q\)（要求\(p<q\)）。如果存在多组这样的向量组合，输出其中任意一组即可。

若不存在这样的向量组合，则输出两个\(-1\)。

Sample Input

5 2

1 0 1 0 1

1 1 0 1 0

0 1 0 1 1

Sample Output

2 3

HINT

这道题的确挺神的，想了几个小时都只能想得到暴力（\(k=2\)的可以二进制压位）。最后还是无奈的自己翻题解自己研究。

以样例为例（\(K = 2\)时）：

首先我们令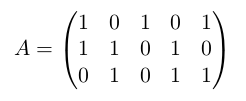

然后我们令\(B\)为\(A\)的转置矩阵（A的行列互换），即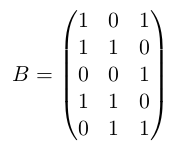

令$$P = A \times B$$

令\(G\)为一个\(n \times n\)的矩阵，里面元素全为\(1\)。

令\(F\)为一个\(n \times n\)的矩阵，除了\(F_{i,i}\)以外的元素全部是\(1\)，并且满足\(F_{i,i}+P_{i,i} = 1\)。

我们再令一个$$T=G-F-P$$。

若\(G_{i,j}=1\)，则向量\(x_{i}\)与向量\(x_{j}\)的内积为\(0\)，\(x_{i}\)与向量\(x_{j}\)为合法解。（注：以上操作均在对\(k\)取模的意义下完成）

但是这样暴力计算矩阵的话无异于暴力。我们可以利用矩阵乘法的性质优化一下。

由于$$T=G-F-P$$

所以我们可以随机一个\(1 \times n\)的矩阵\(X\)，就有$$X \times T=X \times (G-F-P)$$

利用乘法分配律拆开$$X \times T = X \times G-X \times F - X \times P = X \times G-X \times F - X \times A \times B$$

由于我们的\(X\)是一个\(1 \times n\)的矩阵，\(X \times A \times B\)可以在\(O(nd)\)的时间内算出来。

矩阵\(F\)的元素我们只需要计算对角线，所以\(F\)我们可以在\(O(nd)\)的时间内算出来。\(X \times F\)可以在\(O(n)\)的时间内计算出来（\(F\)大部分元素为\(0\)，只需计算对角线）。

同上，\(X \times G\)也可以线性算，所以算出\(X \times T\)的时间是\(O(nd)\)的。

然后我们令\(Q = X \times T\)，若\(Q_{1,i} = 0\)（对\(k\)取模的意义），则\(T\)在第\(i\)行肯定存在元素\(1\)，我们只需单独求出此行的结果即可\(O(nd)\)。

这样\(k = 2\)的我们就可以做了。

\(k=3\)的时候有一点小变化。由于在对\(3\)取模的意义下我们除了\(0,1\)，还可以得到\(2\)。但是仔细观察我们可以发现$$1^{2}=2{2} \equiv 1(mod ; 3)$$。于是就可以做了。

对于向量\(A,B\)的内积\((A,B)\)，我们转而求其平方（\(d=3\)为例）。$$(A,B)^{2}=(a_{1} \times b_{1}+a_{2} \times b_{2}+a_{3} \times b_{3})^{2}$$

将式子拆开我们可以得到

\[(A,B)^{2}=(a_{1}a_{1})(b_{1}b_{1})+(a_{1}a_{2})(b_{1}b_{2})+(a_{1}a_{3})(b_{1}b_{3})+(a_{2}a_{1})(b_{2}b_{1})+(a_{2}a_{2})(b_{2}b_{2})+(a_{2}a_{3})(b_{2}b_{3})+(a_{3}a_{1})(b_{3}b_{1})+(a_{3}a_{2})(b_{3}b_{2})+(a_{3}a_{3})(b_{3}b_{3})
\]

眼熟吧，将\(A,B\)的维度扩展到\(d^{2}\)，其实就是

\[A=[a_{1}a_{1},a_{1}a_{2},a_{1}a_{3},a_{2}a_{1},a_{2}a_{2},a_{2}a_{3},a_{3}a_{1},a_{3}a_{2},a_{3}a_{3}]
\]

\[B=[b_{1}b_{1},b_{1}b_{2},b_{1}b_{3},b_{2}b_{1},b_{2}b_{2},b_{2}b_{3},b_{3}b_{1},b_{3}b_{2},b_{3}b_{3}]
\]

两个新向量的内积。这样就可按照\(k=2\)的做法来做啦！！！

由于常数写大了，不想调试，BZOJ上过不了（时限怎么好像不太对！！！），uoj上被Hack掉了3分。不要在意这些细节。

#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;

#define maxd (110)
#define maxn (100010)
int N,D,K,DD,ori[maxn][maxd],F[maxn],R[maxn],P[maxn],temp[maxd*maxd];

inline int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}

inline int change(int i,int j)
{
	if (K&1)
	{
		int t1 = (j+DD-1)/DD,t2 = j-(t1-1)*DD;
		return ori[i][t1]*ori[i][t2];
	}
	else return ori[i][j];
}

inline bool work()
{
	for (int TTT = 10;TTT;--TTT)
	{
		P[1] = 0;
		for (int i = 1;i <= N;++i) { (P[1] += (R[i] = rand()%K)); if (P[1] >= K) P[1] -= K; }
		for (int i = 2;i <= N;++i) P[i] = P[i-1];
		for (int i = 1;i <= N;++i) { P[i] -= R[i]*F[i]; P[i] %= K; if (P[i] < 0) P[i] += K; }
		for (int i = 1;i <= D;++i)
		{
			temp[i] = 0;
			for (int j = 1;j <= N;++j) temp[i] += R[j]*change(j,i);
			if (temp[i] >= K) temp[i] %= K;
		}
		for (int i = 1;i <= N;++i)
		{
			for (int j = 1;j <= D;++j) P[i] -= temp[j]*change(i,j);
			P[i] %= K; if (P[i] < 0) P[i] += K;
		}
		for (int i = 1;i <= N;++i)
			if (P[i])
			{
				for (int j = 1;j <= N;++j)
				{
					R[j] = 0;
					for (int k = 1;k <= D;++k) (R[j] += change(i,k)*change(j,k));
					R[j] %= K;
					if (!R[j]&&j != i)
					{
						if (i < j) printf("%d %d\n",i,j);
						else printf("%d %d\n",j,i); break;
					}
				}
				return true;
			}
	}
	return false;
}

int main()
{
	freopen("3243.in","r",stdin);
	freopen("3243.out","w",stdout);
	srand(173); scanf("%d %d %d",&N,&D,&K);
	for (int i = 1;i <= N;++i) for (int j = 1;j <= D;++j) ori[i][j] = read()%K;
	if (K == 3) DD = D,D *= D;
	for (int i = 1;i <= N;++i)
	{
		for (int j = 1;j <= D;++j) F[i] += change(i,j)*change(i,j);
		F[i] %= K; F[i] ^= 1;
	}
	if (work()) return 0; else printf("-1 -1");
	fclose(stdin); fclose(stdout);
	return 0;
}

这份是真\(\cdot\)标程

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <ctime>

using namespace std;

const int maxn = 120000;

int n, d, k;
int a[maxn][120], b[120][maxn];
int s[2][maxn], t[maxn], g[maxn];

int read() {
	int num = 0; char ch = getchar();
	while (ch < '0' || ch > '9') ch = getchar();
	while (ch >= '0' && ch <= '9') {
		num = num * 10 + ch - '0';
		ch = getchar();
	}
	return num % k;
}
void find(int o) {
	for (int i = 1; i <= n; i++)
		if (i != o) {
			int sum = 0;
			for (int j = 1; j <= d; j++)
				sum += a[o][j] * a[i][j];
			if (sum % k == 0) {
				printf("%d %d", min(o, i), max(o, i));
				return;
			}
		}
}
void mul(int o) {
	if (o == 1) {
		if (k == 2) {
			memset(t, 0, sizeof(t));
			for (int i = 1; i <= d; i++)
				for (int j = 1; j <= n; j++)
					t[i] = (t[i] + b[i][j] * s[0][j]) & 1;
			memset(s[0], 0, sizeof(s[0]));
			for (int i = 1; i <= n; i++)
				for (int j = 1; j <= d; j++)
					s[0][i] = (s[0][i] + a[i][j] * t[j]) & 1;
		} else {
			memset(t, 0, sizeof(t));
			for (int i = 1; i <= d; i++)
				for (int j = 1; j <= d; j++)
					for (int l = 1; l <= n; l++)
						t[i * d + j] = (t[i * d + j] + b[i][l] * b[j][l] * s[0][l]) % 3;
			memset(s[0], 0, sizeof(s[0]));
			for (int i = 1; i <= n; i++)
				for (int j = 1; j <= d; j++)
					for (int l = 1; l <= d; l++)
						s[0][i] = (s[0][i] + a[i][j] * a[i][l] * t[j * d + l]) % 3;
		}
	}
	else {
		int sum = 0;
		for (int i = 1; i <= n; i++) sum += s[1][i];
		for (int i = 1; i <= n; i++)
			s[1][i] = (sum - (1 - g[i]) * s[1][i]) % k;
	}
}
void solve() {
	srand(241);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= d; j++)
			b[j][i] = a[i][j];

	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= d; j++) {
			g[i] = (g[i] + a[i][j] * a[i][j]) % k;
			if (k == 3) g[i] = (g[i] * g[i]) % 3;
		}
	for (int t = 1; t <= 10; t++) {
		for (int i = 1; i <= n; i++) s[0][i] = rand() & 1;
		for (int i = 1; i <= n; i++) s[1][i] = s[0][i];
		mul(1); mul(2);
		for (int i = 1; i <= n; i++)
			if (s[0][i] != s[1][i]) {
				find(i);
				return;
			}
	}

	printf("-1 -1");
}
int main() {
	freopen("3243.in", "r", stdin);
	freopen("check.out", "w", stdout);

	scanf("%d %d %d", &n, &d, &k);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= d; j++)
			a[i][j] = read();

	solve();

	return 0;
}