Yahoo! Logo ASCII Animation in 462 bytes of C

Last week I put together another obfuscated C program and have been urged by my coworkers to post it publicly. I've made some refinements since posting it to our internal list, so here is the final version (to those who had seen it already: it's one line shorter now, and the angles are less screwy, and the animation is 2 seconds instead of 3). Go ahead, try it:

$ cat >yanim.c
c,p,i,j,n,F=40,k,m;float a,x,y,S=0,V=0;main(){for(;F--;usleep(50000),F?puts(
"\x1b[25A"):0)for(S+=V+=(1-S)/10-V/4,j=0;j<72;j+=3,putchar(10))for(i=0;x=S*(
i-27),i++<73;putchar(c[" ''\".$u$"]))for(c=0,n=3;n--;)for(y=S*(j+n-36),k=0,c
^=(136*x*x+84*y*y<92033)<<n,p=6,m=0;m<8;k++["<[\\]O=IKNAL;KNRbF8EbGEROQ@BSX"
"XtG!#t3!^"]/1.16-68>x*cos(a)+y*sin(a)?k=p,p="<AFJPTX"[m++]-50:k==p?c^=1<<n,
m=8:0)a=(k["O:85!fI,wfO8!yZfO8!f*hXK3&fO;:O;#hP;\"i[by asloane"]-79)/14.64;}
^D
$ gcc -o yanim yanim.c -lm
[warnings which real programmers ignore]
$ ./yanim
[you'll see - show the animation]

                  ...uuuu$$$$$uuuu...                      $$$$$$$uuuuuu
             ..u$$$$$$$$$$$$$$$$$$$$$$$u..                 $$$$$$$$$$$$'
          .u$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$u.              $$$$$$$$$$$$
        .$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$.            $$$$$$$$$$$"
      .$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$.          $$$$$$$$$$$
     u$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$u         $$$$$$$$$$$
   .$$$$$$$                 $$$$$$$$$$$$$$$$$$$$$$$.       $$$$$$$$$$'
   $$$$$$$$$$$$$u.      uu$$$$$''''''''''''''$$$$$$$       $$$$$$$$$$
  $$$$$$$$$$$$$$$$.      $$$$$$..         ..$$$$$$$$$      $$$$$$$$$"
  $$$$$$$$$$$$$$$$$u      "$$$$$$"'    u$$$$$$$$$$$$$      $$$$$$$$$
 u$$$$$$$$$$$$$$$$$$$      '$$$"'    u$$$$$$$$$$$$$$$u     $$$$$$$$$
 $$$$$$$$$$$$$$$$$$$$$.     '"'    u$$$$$$$$$$$$$$$$$$     $$$$$$$$
  $$$$$$$$$$$$$$$$$$$$$u        .u$$$$$$$$$$$$$$$$$$$      $$$$$$$$
  $$$$$$$$$$$$$$$$$$$$$$u      u$$$$$$$$$$$$$$$$$$$$$      $$$$$$$"
  '$$$$$$$$$$$$$$$$$$$$$$      $$$$$$$$$$$$$$$$$$$$$'      $$$$$$$
   "$$$$$$$$$$$$$$$$$$$$$      $$$$$$$$$$$$$$$$$$$$"       ""$$$$$
    '$$$$$$$$$$$$$$$"""""      """""$$$$$$$$$$$$$$'
      "$$$$$$$$$$$$$................$$$$$$$$$$$$"         ..
       '"$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$"'          $$$$$$$u
         '"$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$"'            $$$$$$$'
            '""$$$$$$$$$$$$$$$$$$$$$$$$$""'              .$$$$$$$
                ''"""$$$$$$$$$$$$$"""''                  '"""""$$
                         '''''

It's a 20fps, antialiased ASCII art animation of the Yahoo! logo. If you want to figure out how it works on your own, you're welcome to. Otherwise, read on.

I encourage you to play with the constants in the code: S+=V+=(1-S)/10-V/5 is the underdamped control system for the animation -- S is scale (=1/zoom), V is velocity, and 1/10 and 1/5 are the PD constants. S=0 corresponds to infinite zoom on the first frame. S<0 is funny. F is the frame counter. The 1.16 controls the scale of the polygon rendering (68 is an approximation of 79/1.16 so you have to adjust that too), and 136/84/92033 define the ellipse. The 14.64 is not a tunable parameter, though (it's 46/π, and for a good reason).

The antialiasing is simple: each character consists of three vertically-arranged samples and an 8-character lookup table for each arrangement of three on/off pixels. Each frame consists of 73x24 characters, or 73x72 pixels. The 73 horizontal choice was somewhat arbitrary; I suppose I could have gone up to 79.

The logo is rendered as an ellipse and eight convex polygons using a fairly neat method (I thought) with sub-pixel precision and no frame buffer. It required some design tradeoffs to fit into two printable-character arrays, but it's much less code than rendering triangles to a framebuffer, which is the typical way polygon rasterization is done.

To produce this, first I had to vectorize the "Y!" logo. I did this by taking some measurements of a reference image and writing coordinates down on graph paper. Then I wrote a utility program which takes the points and polygon definitions and turns them into angles and offsets as defined below. [I put the generator code on pastebin until I get can some code highlighting stuff set up for my blog].

The ellipse is fairly standard high-school math: x²/a² + y²/b² < 1. Each point is tested and if it's inside the ellipse, the pixel is plotted. (136x² + 84y² < 92033 was a trivial rearrangement of terms with a and b being the radii of the two axes of the ellipse measured from my source image, scaled to the pixel grid).

Each polygon is made up of a set of separating half-planes (a half-plane being all points on one side of an infinitely long line). If a given point is "inside" all of the half-planes, it's inside the polygon (which only works as long as the polygon is convex) and the pixel is toggled with the XOR operator ^ (thus it handles the "inverse" part inside the ellipse as well as the uninverted exclamation mark without any special cases). Each side of a polygon is defined by the equation ax + by > c. To represent both a and b I use an angle θ so that a = cos(θ) and b = sin(θ) and quantize the angle in π/46 increments — my angles are thus represented from -π to +π as ASCII 33 to 125 — '!' to '}' — with 'O' (ASCII 79) as zero. Then I solve for c, also quantized in scaled increments from -47 to +47, so that the midpoint of the side is considered inside the polygon.

Here's an extremely crude diagram: (I'm writing this on a plane and none of my drawing programs are working. Sorry.)

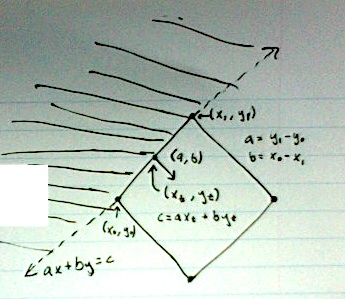
The shaded area is ax + by < c, implying it's outside the polygon, and the dashed line is ax + by = c.

(a,b) form a vector orthogonal to the line segment they represent pointing towards the inside of the polygon, so we can get them directly from the points defining the line segment by taking the vector defining the side — (x₁ - x₀, y₁ - y₀) — and rotating it 90 degrees, resulting in (a, b) = (y₁ - y₀, x₀ - x₁). Then we normalize (a, b) as the actual magnitude doesn't matter, but it will be 1 when we decode the angle and we can compensate with our choice of c later (if ax+by>c, then sax+sby>sc for some scale s>0). Then compute θ = atan2(a,b), quantize to one of our 94 angles, and get our new (a,b) = (cos(θ), sin(θ)).

c is easy to get by directly substituting any of the points making up the line on the side of the polygon into c = ax+by. I use the midpoint of the line segment on the side, (x_t, y_t) = ((x₀ +x₁)/2, (y₀ + y₁)/2), because the angle of the side can be slightly off after we quantize θ, and this evens the errors out across the length of the side.

You'll notice on the first couple frames (you can pause with ^S, resume with ^Q -- xon/xoff) that the bottom section of the 'Y' has little bites taken out of it due to the quantization error in the separating half-plane equations.

It could probably be made somewhat more efficient CPU-wise by careful reordering of the separating plane arrays so that most of the drawing area is rejected first. I didn't get to that in my generator code.

The animation is done by the <ESC>[25A sequence — it moves the cursor up 25 lines in just about any terminal emulation mode. I technically only need to move up 24 lines, but puts is shorter than printf and it implicitly adds a newline. If your terminal isn't at least 26 lines high, though, it does funky things to your scrollback. And usleep is there to limit it to 20fps, which is the only non-ANSI Cism about it.

And then I shrunk the code down by arranging it into clever for loops and taking unorthodox advantage of commas, conditionals, and globals being ints by default in C (which is all par for the course in obfuscated C code). And that pretty much reveals all the secrets as to how it was done.

It would be fairly easy to enhance this with a different movement sequence, or rotation (or any kind of 3D transform, as it's basically just ray-tracing the logo). I just animated the scale to prove the point that it was being rendered dynamically and not just a compressed logo, and kept the animation short and sweet.

I apologize in advance for the various sign errors I'm sure to have made when typing this up, but you get the idea.