DFS序专题

牛客专题之DFS序

简介

dfs序: 每个节点在dfs深度优先遍历中的进出栈的时间序列，也就是tarjan算法中的dfn数组。

画个图理解一下：

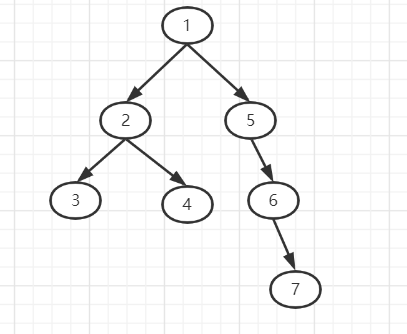
这棵树的dfs序：1 3 2 4 2 5 6 7 6 5 1。

那么这个序列有什么用呢？

通过观察，两个相同数字之间就是以它为根的子树, 也就是说，通过dfs序我们可以得到，这个节点第一次进入栈的时间戳\(l_i\)和第一次出栈的时间戳\(r_i\)。之后我们就可以通过\(l_i\)和\(r_i\)操纵这棵树了。

具体看题：

模板

Military Problem 原CF1006E

题意

你有一棵有\(n\)个节点的树，有\(q\)次询问，每次询问有\((u,k)\)，指从以\(u\)为根的子树出发先序遍历到达的第\(k\)个点是哪一个？如果不存在，输出\(-1\)。

一道模板题。先预处理出每个点的dfs序, 即每个点的\(l_i\)和\(r_i\)。

询问的时候判断是否\(l[u] + k - 1 > r[u]\)， 否则输出\(a[l[u]+k-1]\)就好了。

/*
https://ac.nowcoder.com/acm/problem/112932
https://codeforces.com/problemset/problem/1006/E
*/

#include<bits/stdc++.h>
using namespace std;

#define ll long long
const int mod = 1e9 + 7;
const int maxn = 2e5 + 10;

int a[maxn], cnt = 0;
int l[maxn], r[maxn];
vector<int> G[maxn];

void dfs(int u, int fa){
    l[u] = ++cnt;
    a[cnt] = u;
    for(auto v : G[u]) {
        if(fa == v) continue;
        dfs(v, u);
    }
    r[u] = cnt;
}

int main(){
    int n, q;
    cin >> n >> q;
    for(int i = 2; i <= n; i++) {
        int u; cin >> u;
        G[i].push_back(u);
        G[u].push_back(i);
    }
    dfs(1, 0);
    for(int i = 1; i <= q; i++){
        int u, k;
        cin >> u >> k;
        if(l[u] + k - 1 > r[u]) cout << -1 << endl;
        else cout << a[l[u] + k - 1] << endl;
    }
    return 0;
}

选点

题意

有一棵\(n\)个节点的二叉树，每个节点有权值\(w_i\)，要选尽量多的点，但是得满足以下限制：

对于任意一棵子树，都要满足：

• 如果选了根节点的话，在这棵子树内选的其他的点都要比根节点的值大
• 如果在左子树选了一个点，在右子树中选的其他点要比它小。

思路

读题后可以得到：根的值< 右子树的最大值 < 左子树的最大值, 如果要得到尽量多的点，只需要记录从根 -> 右子树 -> 左子树的dfs序(此处为入栈时间戳\(l_i\))， 在\(l_i\)上找最长上升子序列(没想到。。)即可。

代码

/*
https://ac.nowcoder.com/acm/problem/22494
*/

#include<bits/stdc++.h>
using namespace std;

#define ll long long
const int mod = 1e9 + 7;
const int maxn = 2e5 + 10;

int a[maxn], tot = 0, cnt;
int l[maxn], r[maxn], w[maxn], ans[maxn];
vector<int> G[maxn];

void dfs(int u){
    if(u == 0) return;
    a[++tot] = w[u];
    dfs(r[u]); dfs(l[u]);
}

int main(){
    int n;
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> w[i];
    for(int i = 1; i <= n; i++) cin >> l[i] >> r[i];

    dfs(1);
    ans[++cnt] = a[1];
    // 最长上升子序列贪心O(nlogn)解法
    for(int i = 2; i <= n; i++){
        if(a[i] > ans[cnt]) ans[++cnt] = a[i];
        else{
            int t = lower_bound(ans + 1, ans + 1 + cnt, a[i]) - ans;
            ans[t] = a[i];
        }
    }
    cout << cnt << endl;
    return 0;
}

dfs序+树状数组/线段树

求和

题意

一颗以\(k\)为根有 \(n\) 个节点的树，每个节点有一个点权\(v_i\)。有\(m\) 次操作

• 1 x y 表示将节点 \(x\)的权值加上 \(y\)
• 2 x 表示求以\(x\)为根的子树上所有节点(包括\(x\))的和

思路：

通过 dfs 序将一整棵子树上映射到序列中连续的一段上。问题就变成对数组进行：单点修改，区间查询。用树状数组维护就好了。

代码

/*
https://ac.nowcoder.com/acm/problem/204871
*/
#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define pb push_back

const int maxn = 1e6 + 10;

int l[maxn], r[maxn];
int bits[maxn];
vector<int> G[maxn];
int n, m, k, cnt = 0;

int lowbit(int x){
    return x & (-x);
}
void add(int x, int val){
    while(x < maxn){
        bits[x] += val;
        x += lowbit(x);
    }
}
int query(int x){
    int res = 0;
    while(x){
        res += bits[x];
        x -= lowbit(x);
    }
    return res;
}

void dfs(int u, int fa){
    l[u] = ++cnt;
    for(auto v : G[u]){
        if(v == fa) continue;
        dfs(v, u);
    }
    r[u] = cnt;
}

int a[maxn], op[maxn], b[maxn], val[maxn];

int main(){
    cin >> n >> m >> k;
    for(int i = 1; i <= n; i++) cin >> a[i];
    for(int i = 1; i < n; i++){
        int u, v; cin >> u >> v;
        G[u].push_back(v);
        G[v].push_back(u);
    }
    dfs(k, 0);
    for(int i = 1; i <= n; i++) add(l[i], a[i]);
    for(int i = 0; i < m; i++){
        int op; cin >> op;
        if(op == 1){
            int x, y; cin >> x >> y;
            add(l[x], y);
        }
        else{
            int x; cin >> x;
            cout << (query(r[x]) - query(l[x]-1)) << endl;
        }
    }
    return 0;
}

Propagating tree 原CF383C

题意

一颗以\(1\)为根有 \(n\) 个节点的树，每个节点有一个点权\(a_i\)。有\(m\) 次操作

• 1 x y 表示将 \(x\) 结点权值 \(+val\) ，\(x\) 的儿子权值 \(-val\)，\(x\) 的孙子们 \(+val\), 以此类推。
• 2 x 表示\(x\)的点权

思路

乍一看是树状数组差分，区间修改，单点查询。但是第一个操作搞不定，仔细观察后得到\(1\)操作和每个节点的深度奇偶有关。所以只需判断一下深度，决定修改的值的正负就可以(又没想到。。。)。

代码

/*
https://ac.nowcoder.com/acm/problem/110318
*/
#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define pb push_back

const int maxn = 1e6 + 10;

int l[maxn], r[maxn];
int bits[maxn];
vector<int> G[maxn];
int n, m, k, cnt = 0;
int a[maxn], dep[maxn];

int lowbit(int x){
    return x & (-x);
}
void add(int x, int val){
    while(x < maxn){
        bits[x] += val;
        x += lowbit(x);
    }
}
int query(int x){
    int res = 0;
    while(x){
        res += bits[x];
        x -= lowbit(x);
    }
    return res;
}

void dfs(int u, int fa){
    l[u] = ++cnt;
    dep[u] = dep[fa] + 1;
    for(auto v : G[u]){
        if(v == fa) continue;
        dfs(v, u);
    }
    r[u] = cnt;
}

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++) cin >> a[i];
    for(int i = 1; i < n; i++){
        int u, v; cin >> u >> v;
        G[u].pb(v);
        G[v].pb(u);
    }

    dfs(1, 0);
    // for(int i = 1; i <= n; i++) add(l[i], a[i]);
    for(int i = 0; i < m; i++){
        int op; cin >> op;
        if(op == 1){
            int x, y; cin >> x >> y;
            if(dep[x] & 1){
                add(l[x], y);
                add(r[x] + 1, -y);
            } else {
                add(l[x], -y);
                add(r[x] + 1, y);
            }
        }
        else{
            int x; cin >> x;
            int y = query(l[x]);
            if(dep[x] & 1) cout << a[x] + y << endl;
            else cout << a[x] - y << endl;
        }
    }
    return 0;
}

[华华和月月种树]https://ac.nowcoder.com/acm/problem/23051)

题意

华华和月月一起维护了一棵动态有根树，每个点有一个权值。刚开存档的时候，树上只有 0 号节点，权值为 0 。接下来三种操作：

• \(1\) \(i\) 表示月月氪金使节点\(i\) 长出了一个新的儿子节点，权值为\(0\)，编号为当前最大编号 \(+1\)（也可以理解为，当前是第几个操作 \(1\)，新节点的编号就是多少）。
• \(2\) \(i\) \(a\) 表示华华上线做任务使节点 \(i\) 的子树中所有节点（即它和它的所有子孙节点）权值加 \(a\) 。
• \(3\) \(i\)，华华需要给出 \(i\) 节点此时的权值。

思路

树状数组区间更新单点求值。

操作\(1\)可以将新加的点的减去它的父亲的权值来使得新加的点值为\(0\)。

代码

/*
https://ac.nowcoder.com/acm/problem/23051

https://blog.nowcoder.net/n/0055f19c0e49422786d7b7981a914709
*/

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define pb push_back

const int maxn = 1e6 + 10;

int l[maxn], r[maxn];
int bits[maxn];
vector<int> G[maxn];
int m, cnt = 0;

int lowbit(int x){
    return x & (-x);
}
void add(int x, int val){
    while(x <= cnt + 1){
        bits[x] += val;
        x += lowbit(x);
    }
}
int query(int x){
    int res = 0;
    while(x){
        res += bits[x];
        x -= lowbit(x);
    }
    return res;
}

void dfs(int u){
    l[u] = ++cnt;
    for(auto v : G[u]) dfs(v);
    r[u] = cnt;
}

int a[maxn], op[maxn], b[maxn], val[maxn];

int main(){
    cin >> m;
    for(int i = 0; i < m; i++){
        cin >> op[i] >> a[i];
        if(op[i] == 2) cin >> b[i];
        else if(op[i] == 1){
            G[a[i]].pb(++cnt);
            b[i] = cnt;
        }
    }
    dfs(0);
    // cout << cnt << endl;
    for(int i = 0; i < m; i++){
        if(op[i] == 1) val[l[b[i]]] -= query(l[a[i]]);
        else if(op[i] == 2){
            add(l[a[i]], b[i]);
            add(r[a[i]] + 1, -b[i]);
        }
        else cout << val[l[a[i]]] + query(l[a[i]]) << endl;
    }
    return 0;
}