看动画学算法之:排序-count排序

目录

• 简介
• count排序的例子
• count排序的java实现
• count排序的第二种方法
• count排序的时间复杂度

简介

今天我们介绍一种不需要作比较就能排序的算法：count排序。

count排序是一种空间换时间的算法，我们借助一个外部的count数组来统计各个元素出现的次数，从而最终完成排序。

count排序的例子

count排序有一定的限制，因为外部的count数组长度是和原数组的元素范围是一致的，所以count排序一般只适合数组中元素范围比较小的情况。

我们举一个0-9的元素的排序的例子：3,4,2,5,6,2,4,9,1,3,5。

先看一个动画，看看是怎么排序的：

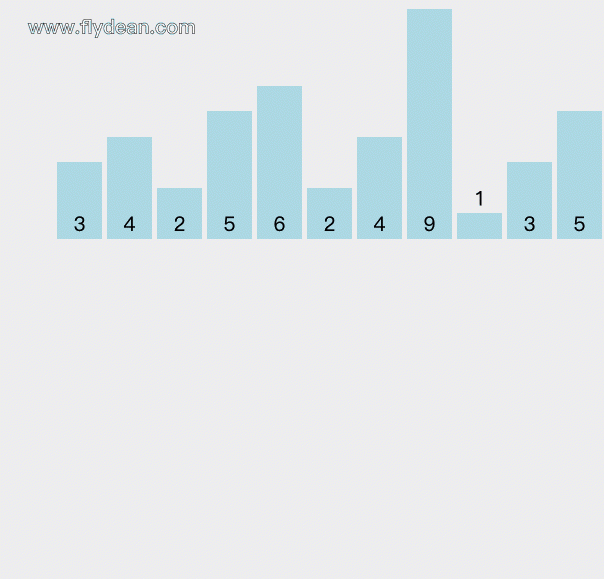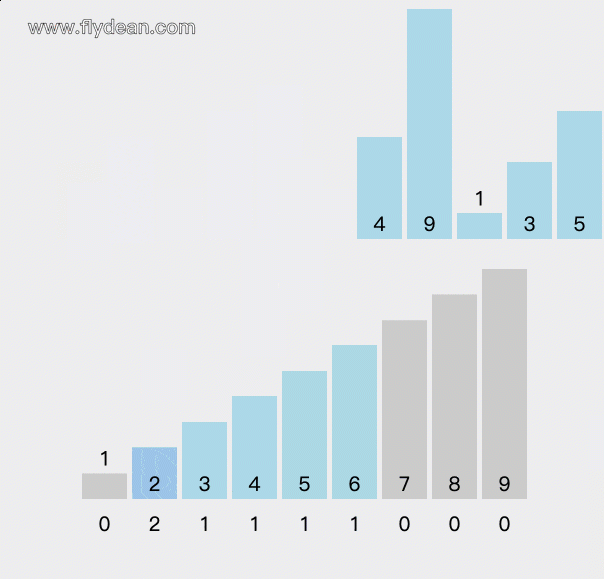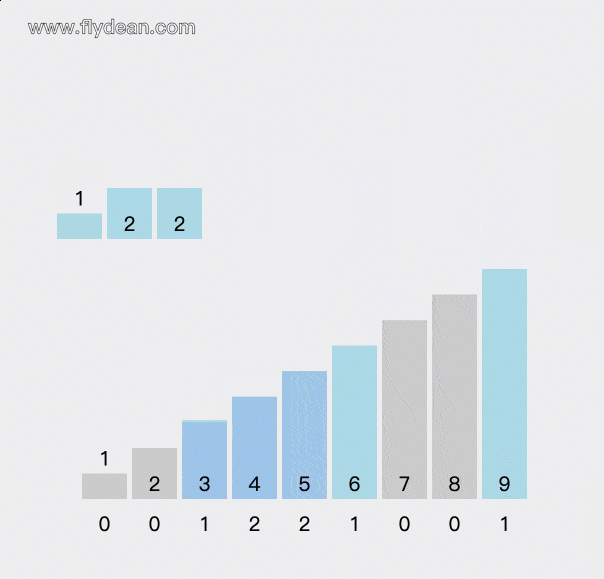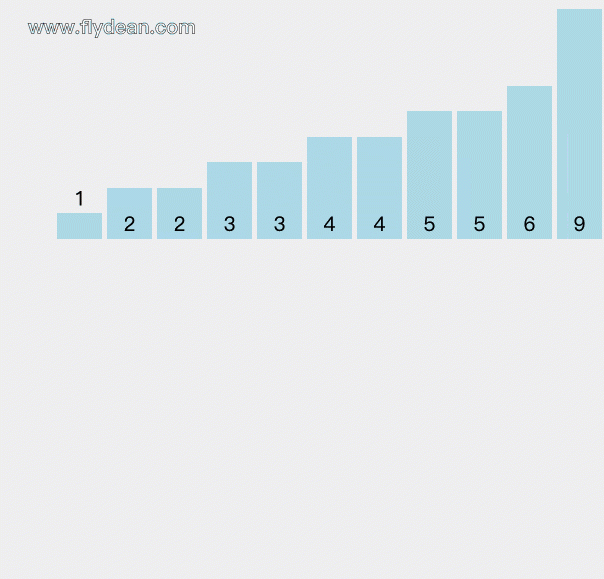
count数组里面存放的是从0到9这些元素出现的次数。

我们遍历原始数组，遇到相应的数字就给相应的count+1。

等所有的元素都count之后，再根据count数组中的值还原排序过后的数组。

count排序的java实现

count排序很简单，我们主要掌握下面两个大的步骤：

1. 遍历原始数组，构建count数组。
2. 根据count数组中的count值，重新构建排序数组。

public class CountingSort {

    public void doCountingSort(int[] array){
        int n = array.length;

        // 存储排序过后的数组
        int output[] = new int[n];

        // count数组，用来存储统计各个元素出现的次数
        int count[] = new int[10];
        for (int i=0; i<10; ++i) {
            count[i] = 0;
        }
        log.info("初始化count值:{}",count);

        // 将原始数组中数据出现次数存入count数组
        for (int i=0; i<n; ++i) {
            ++count[array[i]];
        }
        log.info("count之后count值:{}",count);

        //遍历count，将相应的数据插入output
        int j=0;
        for(int i=0; i<10; i++){
            while(count[i]-- > 0){
                output[j++]=i;
            }
        }
        log.info("构建output之后的output值:{}",output);

        //将排序后的数组写回原数组
        for (int i = 0; i<n; ++i)
            array[i] = output[i];
    }

    public static void main(String[] args) {
        int[] array= {3,4,2,5,6,2,4,9,1,3,5};
        CountingSort countingSort=new CountingSort();
        log.info("countingSort之前的数组为:{}",array);
        countingSort.doCountingSort(array);
    }
}

上面的注释应该很清楚了。

运行的结果如下：

count排序的第二种方法

在我们获得count数组中每个元素的个数之后，其实我们还有另外一个生成结果数组的办法：

// 这里是一个小技巧，我们根据count中元素出现的次数计算对应元素第一次应该出现在output中的下标。
        //这里的下标是从右往左数的
        for (int i=1; i<10; i++) {
            count[i] += count[i - 1];
        }
        log.info("整理count对应的output下标:{}",count);
        // 根据count中的下标，构建排序后的数组
        //插入一个之后，相应的count下标要减一
        for (int i = n-1; i>=0; i--)
        {
            output[count[array[i]]-1] = array[i];
            --count[array[i]];
        }
        log.info("构建output之后的output值:{}",output);

主要分为两步:

第一步我们根据count中元素出现的次数计算对应元素第一次应该出现在output中的下标。这里的下标是从右往左数的。

第二步根据count中的下标，构建排序后的数组，插入一个之后，相应的count下标要减一。

可能不是很好理解，大家可以结合输出结果反复琢磨一下。

count排序的时间复杂度

从上面的代码我们可以看到，count排序实际上只做了少量次数的遍历。所以它的时间复杂度是O(n)。

本文的代码地址：

learn-algorithm

本文已收录于 http://www.flydean.com/algorithm-count-sort/

最通俗的解读，最深刻的干货，最简洁的教程，众多你不知道的小技巧等你来发现！

欢迎关注我的公众号:「程序那些事」,懂技术，更懂你！