MLDS笔记：Optimization

当函数空间覆盖到目标函数时，如何通过优化调整神经网络的参数找到这个目标函数呢？

深度学习中的损失函数是非凸的，非凸优化是个NP-hard问题，如何通过梯度下降来解决这个问题呢？

注意，不同于learning，这里只讨论基于训练集的optimization问题，不考虑在测试集上的表现。

0 为什么说深度学习中的损失函数是非凸的？

对一个神经网络来说至少存在指数级个数的全局最小值，因为你将某一层的神经元重新排列后并不改变损失函数值。



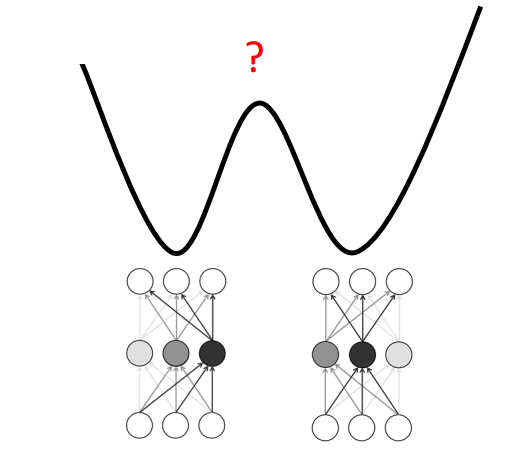
如图0-1所示，线性加权这２组参数所得的loss值不见得变小，说明损失函数是个非凸函数。

但是“非凸”不完全等于“困难”。



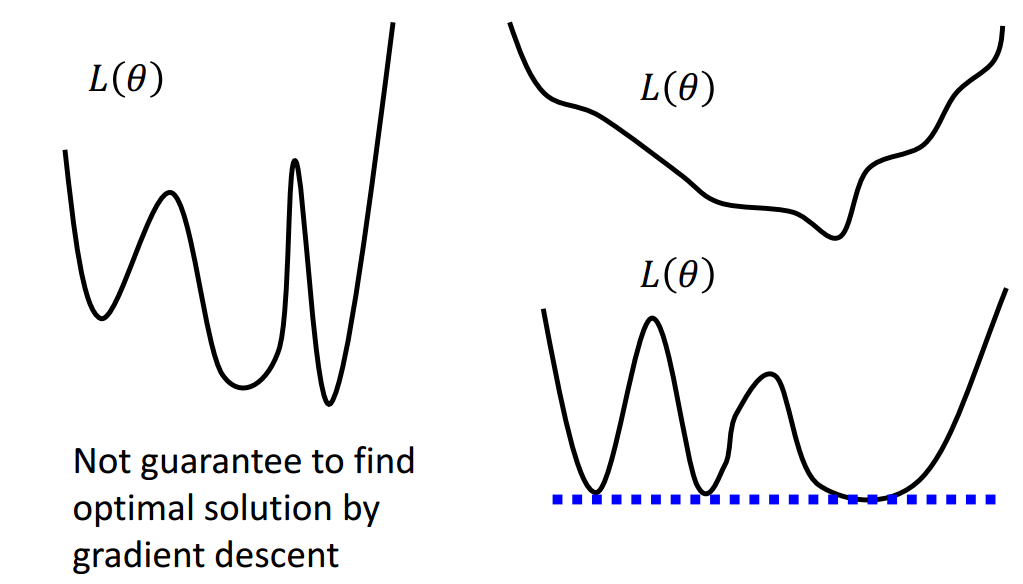
通常来说，非凸函数优化起来很困难，难以用梯度下降找到全局最小值，如图0-2左边所示。

但深度学习中定义的非凸损失函数是否有可能用梯度下降找到全局最小值呢？如图0-2右边所示，有无可能深度学习中定义的非凸损失函数有很多的全局最小值，却没有局部最小值呢？

1 Hessian矩阵

当梯度为０时考虑借助Hessian矩阵进行分析。

人们通常认为训练停止是因为参数到达了关键点，即梯度为０的点。这个点可能是局部最小值点，也可能是鞍点。