LeetCode 周赛 344（2023/05/07）手写递归函数的固定套路

本文已收录到 AndroidFamily，技术和职场问题，请关注公众号 [彭旭锐] 提问。

大家好，我是小彭。

今天下午有力扣杯战队赛，不知道官方是不是故意调低早上周赛难度给选手们练练手。

• 往期周赛回顾：LeetCode 单周赛第 343 场 · 结合「下一个排列」的贪心构造问题

---

周赛概览

T1. 找出不同元素数目差数组（Easy）

标签：模拟、计数、散列表

T2. 频率跟踪器（Medium）

标签：模拟、计数、散列表、设计

T3. 有相同颜色的相邻元素数目（Medium）

标签：模拟、计数、贪心

T4. 使二叉树所有路径值相等的最小代价（Medium）

标签：二叉树、DFS、贪心

---

T1. 找出不同元素数目差数组（Easy）

https://leetcode.cn/problems/find-the-distinct-difference-array/

题解（前后缀分解）

• 问题目标：求每个位置前缀中不同元素个数和后缀不同元素个数的差值；
• 观察数据：存在重复数；
• 解决手段：我们可以计算使用两个散列表计算前缀和后缀中不同元素的差值。考虑到前缀和后缀的数值没有依赖关系，只不过后缀是负权，前缀是正权。那么，我们可以在第一次扫描时将后缀的负权值记录到结果数组中，在第二次扫描时将正权值记录到结果数组中，就可以优化一个散列表空间。

写法 1：

class Solution {
    fun distinctDifferenceArray(nums: IntArray): IntArray {
        val n = nums.size
        val ret = IntArray(n)
        val leftCnts = HashMap<Int, Int>()
        val rightCnts = HashMap<Int, Int>()

        for (e in nums) {
            rightCnts[e] = rightCnts.getOrDefault(e, 0) + 1
        }

        for (i in nums.indices) {
            val e = nums[i]
            leftCnts[e] = leftCnts.getOrDefault(e, 0) + 1
            if (rightCnts[e]!! > 1) rightCnts[e] = rightCnts[e]!! - 1 else rightCnts.remove(e)
            ret[i] = leftCnts.size - rightCnts.size
        }
        return ret
    }
}

写法 2：

class Solution {
    fun distinctDifferenceArray(nums: IntArray): IntArray {
        val n = nums.size
        val ret = IntArray(n)
        val set = HashSet<Int>()

        // 后缀
        for (i in nums.size - 1 downTo 0) {
            ret[i] = -set.size
            set.add(nums[i])
        }

        set.clear()

        // 前缀
        for (i in nums.indices) {
            set.add(nums[i])
            ret[i] += set.size
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ 其中 n 为 nums 数组的长度；
• 空间复杂度：$O(n)$ 散列表空间。

---

T2. 频率跟踪器（Medium）

https://leetcode.cn/problems/frequency-tracker/

题解（散列表）

简单设计题，使用一个散列表记录数字出现次数，再使用另一个散列表记录出现次数的出现次数：

class FrequencyTracker() {

    // 计数
    private val cnts = HashMap<Int, Int>()

    // 频率计数
    private val freqs = HashMap<Int, Int>()

    fun add(number: Int) {
        // 旧计数
        val oldCnt = cnts.getOrDefault(number, 0)
        // 增加计数
        cnts[number] = oldCnt + 1
        // 减少旧频率计数
        if (freqs.getOrDefault(oldCnt, 0) > 0) // 容错
            freqs[oldCnt] = freqs[oldCnt]!! - 1
        // 增加新频率计数
        freqs[oldCnt + 1] = freqs.getOrDefault(oldCnt + 1, 0) + 1
    }

    fun deleteOne(number: Int) {
        // 未包含
        if (!cnts.contains(number)) return
        // 减少计数
        val oldCnt = cnts[number]!!
        if (0 == oldCnt - 1) cnts.remove(number) else cnts[number] = oldCnt - 1
        // 减少旧频率计数
        freqs[oldCnt] = freqs.getOrDefault(oldCnt, 0) - 1
        // 增加新频率计数
        freqs[oldCnt - 1] = freqs.getOrDefault(oldCnt - 1, 0) + 1
    }

    fun hasFrequency(frequency: Int): Boolean {
        // O(1)
        return freqs.getOrDefault(frequency, 0) > 0
    }
}

复杂度分析：

• 时间复杂度：$O(1)$ 每个操作的时间复杂度都是 $O(1)$；
• 空间复杂度：$O(q)$ 取决于增加的次数 $q$。

---

T3. 有相同颜色的相邻元素数目（Medium）

https://leetcode.cn/problems/number-of-adjacent-elements-with-the-same-color/description/

题目描述

给你一个下标从 0 开始、长度为 n 的数组 nums 。一开始，所有元素都是 未染色 （值为 0 ）的。

给你一个二维整数数组 queries ，其中 queries[i] = [indexi, colori] 。

对于每个操作，你需要将数组 nums 中下标为 indexi 的格子染色为 colori 。

请你返回一个长度与 queries 相等的数组 **answer **，其中 **answer[i]是前 i 个操作 之后 ，相邻元素颜色相同的数目。

更正式的，answer[i] 是执行完前 i 个操作后，0 <= j < n - 1 的下标 j 中，满足 nums[j] == nums[j + 1] 且 nums[j] != 0 的数目。

示例 1：

输入：n = 4, queries = [[0,2],[1,2],[3,1],[1,1],[2,1]]
输出：[0,1,1,0,2]
解释：一开始数组 nums = [0,0,0,0] ，0 表示数组中还没染色的元素。
- 第 1 个操作后，nums = [2,0,0,0] 。相邻元素颜色相同的数目为 0 。
- 第 2 个操作后，nums = [2,2,0,0] 。相邻元素颜色相同的数目为 1 。
- 第 3 个操作后，nums = [2,2,0,1] 。相邻元素颜色相同的数目为 1 。
- 第 4 个操作后，nums = [2,1,0,1] 。相邻元素颜色相同的数目为 0 。
- 第 5 个操作后，nums = [2,1,1,1] 。相邻元素颜色相同的数目为 2 。

示例 2：

输入：n = 1, queries = [[0,100000]]
输出：[0]
解释：一开始数组 nums = [0] ，0 表示数组中还没染色的元素。
- 第 1 个操作后，nums = [100000] 。相邻元素颜色相同的数目为 0 。

提示：

• 1 <= n <= 105
• 1 <= queries.length <= 105
• queries[i].length == 2
• 0 <= indexi <= n - 1
• 1 <= colori <= 105

问题结构化

1、概括问题目标

计算每次涂色后相邻颜色的数目个数（与前一个位置颜色相同）。

2、观察问题数据

• 数据量：查询操作的次数是 10^5，因此每次查询操作的时间复杂度不能高于 O(n)。

3、具体化解决手段

• 手段 1（暴力枚举）：涂色执行一次线性扫描，计算与前一个位置颜色相同的元素个数；
• 手段 2（枚举优化）：由于每次操作最多只会影响 (i - 1, i) 与 (i, i + 1) 两个数对的颜色关系，因此我们没有必要枚举整个数组。

题解一（暴力枚举 · TLE）

class Solution {
    fun colorTheArray(n: Int, queries: Array<IntArray>): IntArray {
        // 只观察 (i - 1, i) 与 (i, i + 1) 两个数对
        if (n <= 0) return intArrayOf(0) // 容错

        val colors = IntArray(n)
        val ret = IntArray(queries.size)

        for (i in queries.indices) {
            val j = queries[i][0]
            val color = queries[i][1]
            if (j < 0 || j >= n) continue // 容错
            colors[j] = color
            for (j in 1 until n) {
                if (0 != colors[j] && colors[j] == colors[j - 1]) ret[i] ++
            }
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n^2)$ 每个操作的时间复杂度都是 O(n)；
• 空间复杂度：$O(n)$ 颜色数组空间。

题解二（枚举优化）

class Solution {
    fun colorTheArray(n: Int, queries: Array<IntArray>): IntArray {
        // 只观察 (i - 1, i) 与 (i, i + 1) 两个数对
        if (n <= 0) return intArrayOf(0) // 容错

        val colors = IntArray(n)
        val ret = IntArray(queries.size)

        // 计数
        var cnt = 0
        for (i in queries.indices) {
            val j = queries[i][0]
            val color = queries[i][1]
            if (j < 0 || j >= n) continue // 容错
            // 消除旧颜色的影响
            if (colors[j] != 0 && j > 0 && colors[j - 1] == colors[j]) cnt--
            // 增加新颜色的影响
            if (colors[j] != 0 && j < n - 1 && colors[j] == colors[j + 1]) cnt--
            if (color != 0) { // 容错
                colors[j] = color
                if (j > 0 && colors[j - 1] == colors[j]) cnt++
                if (j < n - 1 && colors[j] == colors[j + 1]) cnt++
            }
            ret[i] = cnt
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ 每个操作的时间复杂度都是 O(1)；
• 空间复杂度：$O(n)$ 颜色数组空间。

相似题目：

• 567. 字符串的排列

---

T4. 使二叉树所有路径值相等的最小代价（Medium）

https://leetcode.cn/problems/make-costs-of-paths-equal-in-a-binary-tree/

问题描述

给你一个整数 n 表示一棵 满二叉树 里面节点的数目，节点编号从 1 到 n 。根节点编号为 1 ，树中每个非叶子节点 i 都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1 。

树中每个节点都有一个值，用下标从 0 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1 个节点的值。每次操作，你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。

注意：

• 满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个节点，且所有叶子节点距离根节点距离相同。
• 路径值 指的是路径上所有节点的值之和。

示例 1：

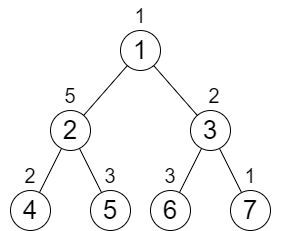
输入：n = 7, cost = [1,5,2,2,3,3,1]
输出：6
解释：我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

示例 2：

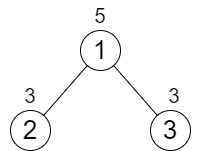
输入：n = 3, cost = [5,3,3]
输出：0
解释：两条路径已经有相等的路径值，所以不需要执行任何增加操作。

提示：

• 3 <= n <= 105
• n + 1 是 2 的幂
• cost.length == n
• 1 <= cost[i] <= 104

问题结构化

1、概括问题目标

计算将所有「根到叶子结点的路径和」调整到相同值的操作次数。

2、分析问题要件

在每一次操作中，可以提高二叉树中某个节点的数值，最终使得该路径和与所有二叉树中其他所有路径和相同。

3、观察问题数据

• 满二叉树：输入数据是数组物理实现的二叉树，二叉树每个节点的初始值记录在 cost 数组上；
• 数据量：输入数据量的上界为 10^5，这要求算法的时间复杂度不能高于 O(n^2)；
• 数据大小：二叉树节点的最大值为 10^4，即使将所有节点都调整到 10^4 路径和也不会整型溢出，不需要考虑大数问题。

4、提高抽象程度

• 最大路径和：由于题目只允许增加节点的值，所以只能让较小路径上的节点值向较大路径上的节点值靠；
• 公共路径：对于节点「2」的子节点「4」和「5」来说，它们的「父节点和祖先节点走过的路径」必然是公共路径。也就是说，无论从根节点走到节点「2」的路径和是多少，对节点 A 和节点 B 的路径和的影响是相同的。
• 是否为决策问题：由于每次操作可以调整的选择性很多，因此这是一个决策问题。

5、具体化解决方案

如何解决问题？

结合「公共路径」思考，由于从根节点走到节点「2」的路径和对于两个子节点的影响是相同的，因此对于节点「2」来说，不需要关心父节点的路径和，只需要保证以节点「2」为根节点的子树上所有路径和是相同的。这是一个规模更小的相似子问题，可以用递归解决。

示意图

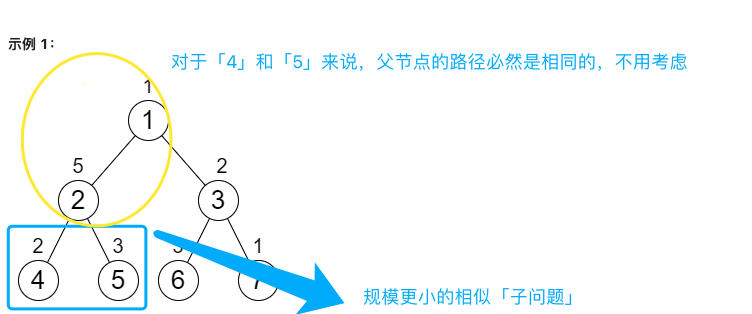
如何实现递归函数？

• 思考终止条件：当前节点为叶子节点时，由于没有子路径，所以直接返回；
• 思考小规模问题：当子节点为叶子节点时，我们只需要保证左右两个叶子节点的值相同（如示例 1 中将节点「4」的值增加到 3）。由于问题的输入数据是满二叉树，所以左右子节点必然同时存在；
• 思考大规模问题：由于我们保证小规模子树的路径和相同，所以在对比两个子树上的路径和时，只需要调大最小子树的根节点。

至此，我们的递归函数框架确定：

全局变量 int ret
// 返回值：调整后的子树和
fun dfs (i) : Int {
		val sumL = dfs(L)
		val sumR = dfs(R)
		ret += max(sumL, sumR) - min(sumL, sumR)
		return cost[i] + max(sumL, sumR)
}

6、是否有优化空间

我们使用递归自顶向下地分解子问题，再自底向上地求解原问题。由于这道题的输入是数组形式的满二叉树，对于数组实现的二叉树我们可以直接地从子节点返回到父节点，而不需要借助「递归栈」后进先出的逻辑，可以翻译为迭代来优化空间。

7、答疑

虽然我们保证子树上的子路径是相同的，但是如何保证最终所有子路径都和「最大路径和」相同？

由于我们不断地将左右子树的路径和向较大的路径和对齐，因此最终一定会将所有路径对齐到最大路径和。

为什么算法的操作次数是最少的？

首先，由于左右子树存在「公共路径」，因此必须把左右子树的子路径和调整到相同数值，才能保证最终所有子路径和的长度相同。

其次，当在大规模子树中需要增大路径和时，在父节点操作可以同时作用于左右子路径，因此在父节点操作可以节省操作次数，每个子树只关心影响当前子树问题合法性的因素。

题解一（DFS）

根据「问题结构化」分析的递归伪代码实现：

class Solution {

    private var ret = 0

    fun minIncrements(n: Int, cost: IntArray): Int {
        dfs(n, cost, 1)
        return ret
    }

    // i : base 1
    // cost : base 0
    // return: 调整后的子路径和
    private fun dfs(n: Int, cost: IntArray, i: Int): Int {
        // 终止条件
        if (i > n / 2) return cost[i - 1] // 最后一层是叶子节点
        // 子问题
        val leftSum = dfs(n, cost, i * 2)
        val rightSum = dfs(n, cost, i * 2 + 1)
        // 向较大的子路径对齐
        ret += Math.max(leftSum, rightSum) - Math.min(leftSum, rightSum)
        return cost[i - 1] + Math.max(leftSum, rightSum)
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ 其中 n 为 节点数，每个节点最多访问 1 次；
• 空间复杂度：$O(lgn)$ 递归栈空间，由于输入是满二叉树，所以递归栈深度最大为 lgn。

题解二（迭代）

由于输入数据是满二叉树，而且是以数组的形式提供，因此我们可以跳过递归分解子问题的过程，直接自底向上合并子问题：

class Solution {
    fun minIncrements(n: Int, cost: IntArray): Int {
        var ret = 0
        // 从叶子的上一层开始
        for (i in n / 2 downTo 1) {
            ret += Math.abs(cost[i * 2 - 1] - cost[i * 2])
            // 借助 cost 数组记录子树的子路径和
            cost[i - 1] += Math.max(cost[i * 2 - 1], cost[i * 2])
        }
        return ret
    }
}

复杂度分析：

• 时间复杂度：$O(n)$ 其中 n 为 节点数，每个节点最多访问 1 次；
• 空间复杂度：$O(1)$ 仅使用常量级别空间。

---

往期回顾

• LeetCode 单周赛第 343 场 · 结合「下一个排列」的贪心构造问题
• LeetCode 单周赛第 342 场 · 把问题学复杂，再学简单
• LeetCode 双周赛第 102 场· 这次又是最短路。
• LeetCode 双周赛第 101 场 · 是时候做出改变了！