怎么理解相互独立事件？真的是没有任何关系的事件吗？《考研概率论学习之我见》 -by zobol

1.从条件概率的定义来看独立事件的定义

2.从古典概率的定义来看独立事件的定义

3.P(A|B)和P(A)的关系是什么？

4.由P(AB)=P(A)P(B)推出“独立”

5.从韦恩图来看独立事件的定义

6.为什么多个事件两两独立推不出相互独立

7.在考研古典概率中，有一个P(A|B)=P(A)就可以推出两者是独立事件吗？

8.在考研中，独立事件可以看作是“独立”的吗？

1.从条件概率的定义来看独立事件的定义

在考研古典概率中，我们最初都是通过条件概率公式来定义独立事件的。

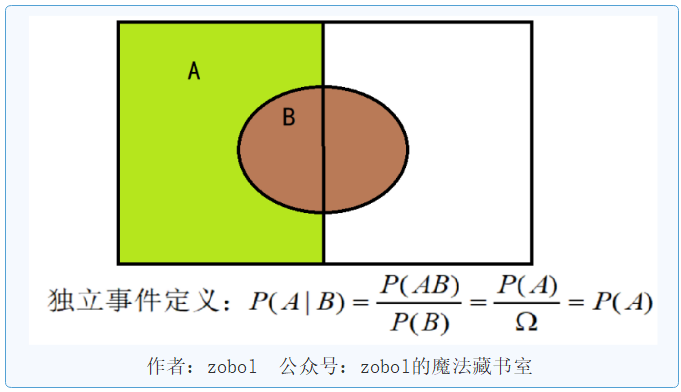
这从条件概率的角度来理解就是在条件B的情况下，A发生的概率与之前相比不变。

所以我们常常理解成，如果两个事件互为独立事件，则B的发生对A没有影响。但这种理解，其实是有谬误的，因为并不是没有影响，只是影响没有体现在比例值上！。

也有一种看法是，B的发生让A的事件发生概率保持不变，保持不变本身也可以看作是一种影响，这种思路也可以理解成：

B发生的同时，A跟着一起发生的概率等于全集中随机选取一个样本点属于A的概率

从这个角度来看，似乎独立事件也不是那么独立，条件概率值等于全集发生概率值，似乎还约束了两个事件之间的关系。不过导致这一切发生的根源还要从古典概率来入手。

2.从古典概率的定义来看独立事件的定义

因为古典概率的定义是根据分式比例值定义的，条件概率的定义也是根据比例值定义的，这就导致一个问题就是3/5=6/10。

原来之所以在事件B的条件约束下，事件A的发生概率没有变，是因为：

分子和分母被缩小了相同的比例

所以我们能说事件B的条件对事件A发生没有影响吗？不能！

我们只能说事件B的条件对事件A的发生概率没有影响！

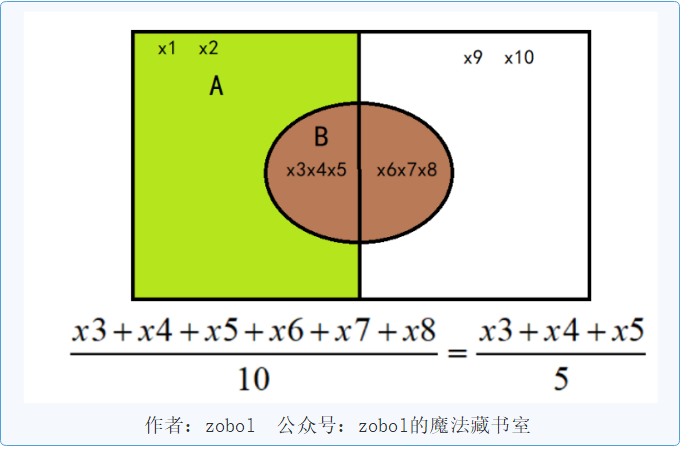
很明显条件A让B的样本点中的x6,x7,x8都被排除在外了，所以是造成了影响，但是对概率值是没有影响的，因为概率值是一个比例值，3/5和6/10是一样大的。

从这一步似乎我们可以看出，为什么多事件的独立性，两两独立推不出相互独立。这是因为，样本点之间有重合的，独立事件定义中的条件概率可以看作是对样本空间和事件B进行了等比例约束。这种约束，在多事件中，可能有重合的样本点，这就导致等比例约束被打破了。

3.P(A|B)和P(A)的关系是什么？

首先它们不在一个样本空间中，所以根本不能看做是一个事件（包含的样本点数量也不一样），实际上条件概率更应该看作是一个比例值，而不是一个事件。

在考研-古典概率中，如果我们可以得到P(A|B)=P(A)或P(B|A)=P(B)中的任何一个，我们就可以推导出这俩一定属于独立事件。

除此之外，P(A|B)和P(A)之间的其他关系式，都是没有太多意义的，不过利用其推出的另外一个关系式用处更大，那就是P(AB)=P(A)P(B)

4.由P(AB)=P(A)P(B)推出“独立”

我们之前是利用条件概率来定义独立事件，我们讨论条件概率的定义是用来解决交事件的计算，这里我们把独立事件也联系进来。

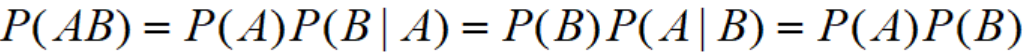
两个概率值相乘其实没什么实际意义，一般来讲，乘法运算表明了两个事件的发生逻辑关系，所以这里也体现了前者的发生对后者没有影响。因此从P(AB)=P(A)P(B)中，我们更可以看出来一种独立性出现。

实际中，独立性也常用来计算交事件的概率，毕竟如果两个事件之间“没有影响”，计算同时发生的概率值就方便很多，只需要直接相乘就可以，这个我们不学独立性，也会计算。

5.从韦恩图来看独立事件的定义

说实话，如果两个事件之间真的没有任何联系，那其实没法用韦恩图来表示，因为韦恩图的基本单位-样本点事件，之间都是互斥事件，所以你画出两个事件之间，都是一定存在某些联系的。不过，上文我们也讲了，不是没有联系，只是这种联系没有体现在概率值上。

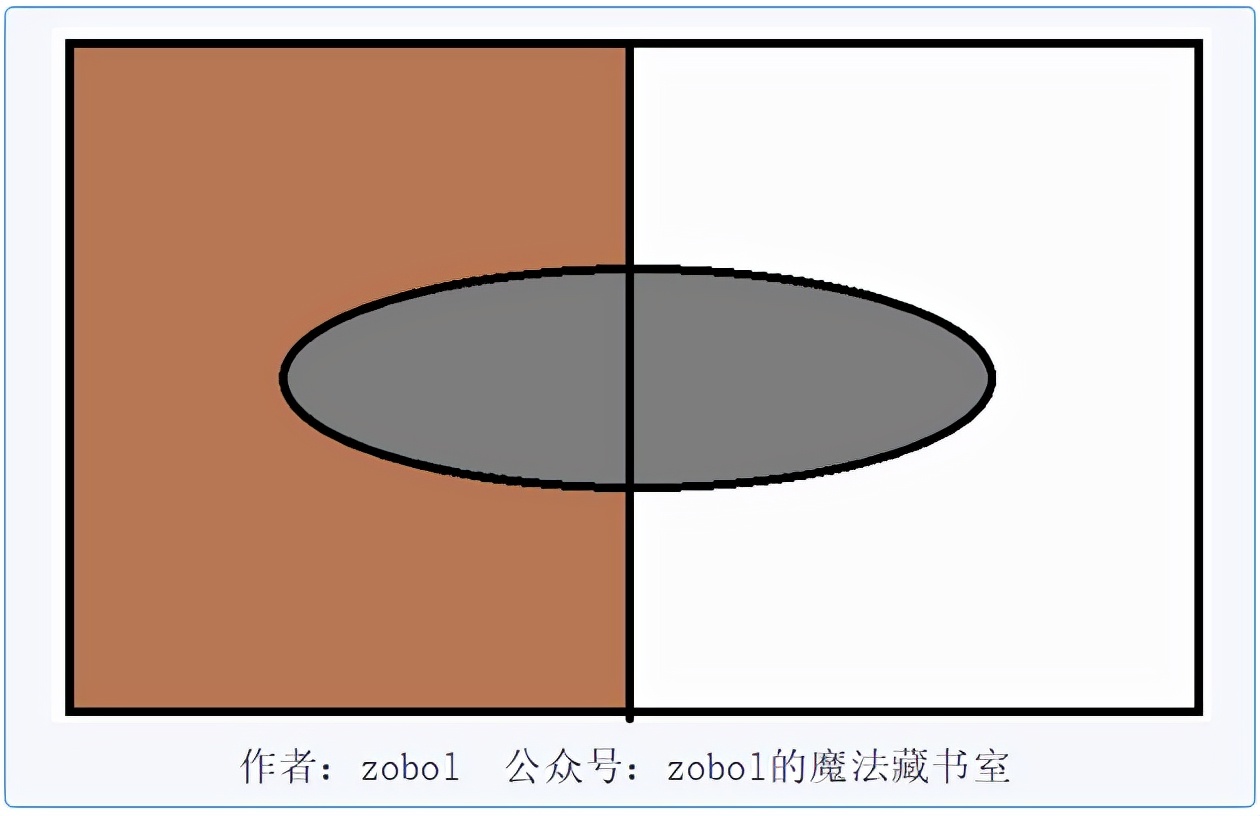
所以我们依然可以简单的画出来，只要注意全部等比例缩小相同倍数即可。

6.为什么多个事件两两独立推不出相互独立

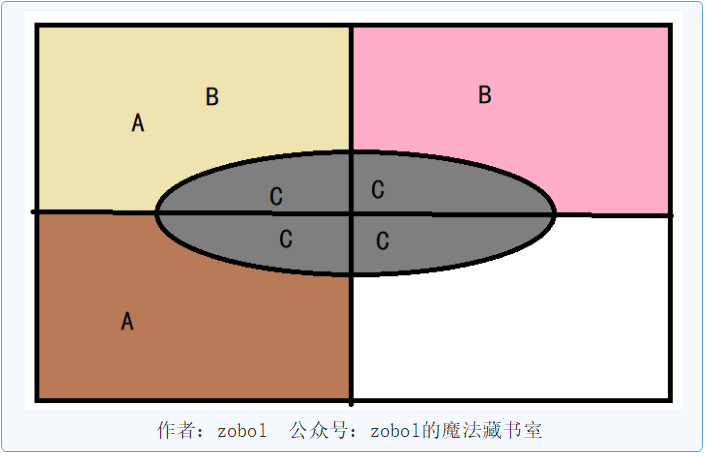
因为等比例缩放，之间的样本点可能有重复的，导致虽然任意选出两个事件，都是构成独立事件的，但全集和事件C的缩放，可能不再成比例了。

也就是推不出P(ABC)=P(A)P(B)P(C)

多个事件，相互独立可以推出两两独立，但两两独立推不出相互独立，也可以从波罗梅奥环中看出来：

7.在考研古典概率中，有一个P(A|B)=P(A)就可以推出两者是独立事件吗？

可以，我们可以从公式中推导出来，也可以利用古典概率定义的集合性质-交换律来想清楚，也可以用韦恩图来看出来。

因此我们只要看到P(A|B)=P(A)，P(A|B)=P(A)，P(AB)=P(A)P(B)任意一个，就可以认为是独立事件。

8.在考研中，独立事件可以看作是“独立”的吗？

可以的，只要在考研中，如果你遇到任何两个事件中存在一定关系，哪怕是非常复杂不好用或与非来表示的，那也一定不是独立事件，构不成独立事件的三个等式。