数据库SQL---范式

1、数据冗余导致的问题：冗余存储、更新异常、插入异常、删除异常。

2、函数依赖：一种完整性约束。

在关系模式r(R)中，α属于R，β属于R。

1）α函数确定β（β函数依赖于α）：记作α→β，对于任意合法关系r及其中任两个元组t_i和t_j，i≠j，若t_i[α]=t_j[α]，则t_i[β]=t_j[β]。

2）非平凡函数依赖和平凡函数依赖：若α→β，但β不属于α，则称α→β是非平凡函数依赖；否则，若β不属于α，则称α→β是平凡函数依赖。

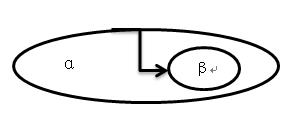
非平凡函数依赖                                                       平凡函数依赖

3）完全函数依赖和部分函数依赖：α→β是非平凡函数依赖，若对任意的γ含于α，γ→β都不成立，则称α→β是完全函数依赖，简称完全依赖；否则，若存在非空的γ含于α，使γ→β成立，则称α→β是部分函数依赖，简称部分依赖。

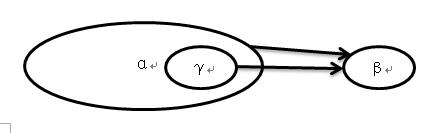
部分依赖α→β的依赖图

4）传递函数依赖

γ属于R，若α→β，β→γ，则必存在函数依赖α→γ，若α→β，β→γ和α→γ都是非平凡函数依赖，且β不依赖于α，则称α→γ是传递函数依赖，简称传递依赖。

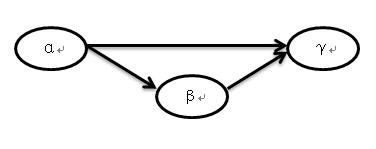
传递依赖α→γ的依赖图

3、函数依赖集闭包

1）逻辑蕴涵：若给定函数依赖集F，可以证明其他函数依赖也成立，则称这些函数依赖被F逻辑蕴涵。

2）闭包：令F为一函数依赖集，F逻辑蕴涵的所有函数依赖组成的集合称为F的闭包，记为F⁺。

3）属性集A的闭包：令r(R)为关系模式，F为属性依赖集，A属于R的属性集，则称在函数依赖集F下由A函数确定的所有属性的集合为F下属性集A的闭包，记为A⁺。

4）Armstrong公理及推论（可直接计算F⁺）

（1）自反律：若存在β属于α，则有α→β。

（2）增补律：若存在α→β，则有γα→γβ。

（3）传递律：若存在α→β且β→γ，则有α→γ。

（4）合并律：若存在α→β且α→γ，则有α→βγ。

（5）分解律：若存在α→βγ，则有α→β和α→γ。

（6）伪传递律：若存在α→β且βγ→δ，则有αγ→δ。

4、范式（关系模式要满足的条件）

1）目的：消除存储异常、减少数据冗余、保证数据完整性和存储效率。

2）基于函数依赖理论，范式的分类：

（1）第一范式（1NF）---码

如果一关系模式r(R)的每个属性对应的域值都是不可分的，则称r(R)属于第一范式。

目标：将基本数据划分成称为实体集或表的逻辑单元，当设计好每个实体后，需要为其指定主码。

empno	ename	address
		province	city	street

非规范化的关系模式（地址的值域可分）

empno

ename

province

city

street

1NF规范化后的关系模式

（2）第二范式（2NF)---全部是码

如果一关系模式r(R)，α属于r(R)，若α包含在r(R)的摸个候选码中，则称α为主属性，否则α非主属性。

如果一关系模式r(R)属于第一范式，且所有非主属性都完全函数依赖于r(R)的候选码，则称r(R)属于第二范式。

目标：将只部分依赖于候选码（即依赖于候选码的部分属性）的非主属性通过关系模式分解移到其他表中去。

（3）第三范式（3NF)---仅仅是码

如果一关系模式r(R)属于第二范式，且所有非主属性都直接函数依赖于r(R)的候选码，且非主属性之间不存在依赖关系（即不存在非主属性传递依赖于候选码），则称r(R)属于第三范式。

目标：将只部分依赖于候选码（即依赖于候选码的部分属性）的非主属性通过关系模式分解移到其他表中去。

（4）Boyce-Codd范式（BCNF)

给定关系模式r(R)及函数依赖集F，若F⁺中的所有函数依赖α→β（α属于R，β属于R）至少满足下列条件之一：α→β是平凡函数依赖（即β属于α）、α是r(R)的一个超码（即α⁺包含R的全部属性），则称r(R)属于Boyce-Codd范式。