求矩阵最少(或最多)路径和(python实现)
1.递归方式
求最短,最终状态即右下角
f(v, i, j) = min(f(v, i - 1, j), f(v, i, j - 1)) + v[i][j]
最长只需将min改为max即可
import numpy as np
# i:行
# j:列
# v:矩阵
def f(v, i, j):
if i == 0 and j == 0:
return v[0][0]
elif i == 0:
return f(v, i, j - 1) + v[i][j]
elif j == 0:
return f(v, i - 1, j) + v[i][j]
else:
return min(f(v, i - 1, j), f(v, i, j - 1)) + v[i][j]
v = np.array([[1, 3, 5, 9], [8, 1, 3, 4], [5, 0, 6, 1], [8, 8, 4, 0]])
print(f(v, 3, 3))
2.递推方式
注意到只能往右或往下,可以想象,每下一层是右方或下方,而矩阵中,可以想象是以平行与对角线方向为一层,一层层从左上角到右下角递推
即运行一半为如此:
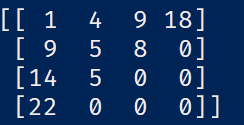
运行完全部为如此

而一层层,每层每一单元取左或上累计最少的数加上本身
即
f[i][j] = min(f[i - 1]f[j], f[i]f[j - 1]) + v[i][j]
因此:代码如下:
import numpy as np
# i:行
# j:列
# v:矩阵
def f(v, n):
s = np.array([[0] * n] * n)
for p in range(n):
for i in range(p + 1):
j = p - i
if i == 0 and j == 0:
s[0][0] = v[0][0]
elif i == 0:
s[0][j] = s[0][j - 1] + v[0][j]
elif j == 0:
s[i][0] = s[i - 1][0] + v[i][0]
else:
s[i][j] = min(s[i - 1][j], s[i][j - 1]) + v[i][j]
limit = 0
for p in range(n, 2 * n - 1):
limit += 1
for i in range(limit, p - limit + 1):
j = p - i
if i == 0 and j == 0:
s[0][0] = v[0][0]
elif i == 0:
s[0][j] = s[0][j - 1] + v[0][j]
elif j == 0:
s[i][0] = s[i - 1][0] + v[i][0]
else:
s[i][j] = min(s[i - 1][j], s[i][j - 1]) + v[i][j]
return s
v = np.array([[1, 3, 5, 9], [8, 1, 3, 4], [5, 0, 6, 1], [8, 8, 4, 0]])
print(f(v, 4))
最后统计出的矩阵的右下即为最少路径和(s[n-1][n-1])
而通过返回s[n-1],我们可以看到路径,从左上角开始,取每一层最小值(不可单独面对方向,可能会陷入陷阱,中途进入错误路径),代码实现如下:
def view(s, n):
string = ''
for p in range(n):
min = 0
for i in range(p + 1):
j = p - i
if min == 0:
min = s[i][j]
elif min > s[i][j]:
min = s[i][j]
string += str(min) + '->'
limit = 0
for p in range(n, 2 * n - 1):
limit += 1
min = 0
for i in range(limit, p - limit + 1):
j = p - i
if min == 0:
min = s[i][j]
elif min > s[i][j]:
min = s[i][j]
if p == (2 * n - 2):
string += str(min)
else:
string += str(min) + '->'
return string
原矩阵:

运行效果:
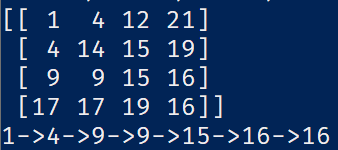
求矩阵最少(或最多)路径和(python实现)的更多相关文章
- 【python实例】要求输出字符串中最少一个最多八个的所有字符串组合(连续)
""" 题目:字符串str="ABCDEFGHIJK",要求输出最少一个最多八个的所有组合(向后连续字母) 输出如下: A [0::] AB ABC ...
- 市场清仓价格算法 python求矩阵不同行不同列元素和的最大值
问题描述 求矩阵不同行不同列元素和的最大值(最小值) 问题求解 1.通过scipy库求解 scipy.optimize库中的linear_sum_assignment方法可以求解 输入一个矩阵,参数m ...
- POJ 1151 Atlantis(经典的线段树扫描线,求矩阵面积并)
求矩阵的面积并 采用的是区间更新 #include <iostream> #include <stdio.h> #include <string.h> #inclu ...
- HDU 1828 / POJ 1177 Picture (线段树扫描线,求矩阵并的周长,经典题)
做这道题之前,建议先做POJ 1151 Atlantis,经典的扫描线求矩阵的面积并 参考连接: http://www.cnblogs.com/scau20110726/archive/2013/0 ...
- Comprehensive learning path – Data Science in Python深入学习路径-使用python数据中学习
http://blog.csdn.net/pipisorry/article/details/44245575 关于怎么学习python,并将python用于数据科学.数据分析.机器学习中的一篇非常好 ...
- MATLAB中求矩阵非零元的坐标
MATLAB中求矩阵非零元的坐标: 方法1: index=find(a); [i,j]=ind2sub(size(a),index); disp([i,j]) 方法2: [i,j]=find(a> ...
- POJ 1151 Atlantis 求矩阵面积并 扫描线 具体解释
题意: 给定n个矩阵的左下角和右上角坐标,求矩阵面积并(矩阵总是正放的,即与x轴y轴都平行) 思路: 扫描线裸题 http://www.cnblogs.com/fenshen371/p/3214092 ...
- 求矩阵中各列数字的和 Exercise08_01
import java.util.Scanner; /** * @author 冰樱梦 * 时间:2018年12月 * 题目:求矩阵中各列数字的和 * */ public class Exercise ...
- 求矩阵主对角线元素的和 Exercise08_02
import java.util.Scanner; /** * @author 冰樱梦 * 时间:2018年12月 * 题目:求矩阵主对角线元素的和 * */ public class Exercis ...
随机推荐
- 电信资源管理系统:基于 H5 叠加 OpenLayers3 GIS
前言 通过结合 HTML5 和 OpenLayers 可以组合成非常棒的一个电信地图网络拓扑图的应用,形成的效果可以用来作为电信资源管理系统,美食定位分享软件,片区找房,绘制铁轨线路等等,各个领域都能 ...
- golang的生产者消费者模型示例
package main import "fmt" func Producer(ch chan int) { for i := 1; i <= 10; i++ { ch &l ...
- 05-03 主成分分析(PCA)
目录 主成分分析(PCA) 一.维数灾难和降维 二.主成分分析学习目标 三.主成分分析详解 3.1 主成分分析两个条件 3.2 基于最近重构性推导PCA 3.2.1 主成分分析目标函数 3.2.2 主 ...
- e课表项目第二次冲刺周期第四天
昨天干了什么? 昨天,我在网上搜集了相关的资料,即连接安卓自带的数据库,查询了连接的方法,然后在电脑上,做了简单的练习,发现可以用,所以对我们的软件进行数据库的连接,设置了完成按钮的活动,即先保存到数 ...
- 移动端自动化测试Appium 从入门到项目实战Python版☝☝☝
移动端自动化测试Appium 从入门到项目实战Python版 (一个人学习或许会很枯燥,但是寻找更多志同道合的朋友一起,学习将会变得更加有意义✌✌) 说到APP自动化测试,Appium可是说是非常流 ...
- docker的使用之镜像命令
说明 Docker运行容器前需要本地存在对应的镜像 ,如果镜像不存在本地,Docker会从镜像仓库下载 获取镜像 通过网址可以找到目标镜像 https://hub.docker.com/explore ...
- Java零基础手把手系列:HashMap排序方法一网打尽
HashMap的排序在一开始学习Java的时候,比较容易晕,今天总结了一些常见的方法,一网打尽.HashMap的排序入门,看这篇文章就够了. 1. 概述 本文排序HashMap的键(key)和值(va ...
- Spring Cloud Alibaba学习笔记(3) - Ribbon
1.手写一个客户端负载均衡器 在了解什么是Ribbon之前,首先通过代码的方式手写一个负载均衡器 RestTemplate restTemplate = new RestTemplate(); // ...
- Vue-CLI 项目中相关操作
0830总结 Vue-CLI 项目中相关操作 一.前台路由的基本工作流程 目录结构 |vue-proj | |src | | |components | | | |Nav.vue | | |views ...
- Windows系统调用中API的3环部分(依据分析重写ReadProcessMemory函数)
Windows内核分析索引目录:https://www.cnblogs.com/onetrainee/p/11675224.html Windows系统调用中API的3环部分 一.R3环API分析的重 ...
