江苏 徐州邀请赛 icpc B Array dp 滚动数组模板

题目

题目描述

JSZKC is the captain of the lala team. 
There are N girls in the lala team. And their height is [1,N] and distinct. So it means there are no two girls with a same height. 
JSZKC has to arrange them as an array from left to right and let h[i] be the height of the ith girl counting from the left. After that, he can calculate the sum of the inversion pairs. A inversion pair counts if h[i]>h[j] with i

输入

The input file contains several test cases, each of them as described below. 
The first line of the input contains two integers N and K (1 ≤ N ≤ 5000, 0 ≤ K ≤ 5000), giving the number of girls and the pairs that JSZKC asked. 
There are no more than 5000 test cases.

输出

An integer in one line for each test case, which is the number of the plans mod 1000000007.

样例输入

3 2
3 3

• 1
• 2

样例输出

2
1

• 1
• 2

---

题意

  问你1~n的所有排列中有多少种排列拥有k对逆序数。

分析：

dp[i][j]代表长度为ii的排列有jj对逆序数的方案数，考虑放第ii个数的时候，前面i−1i−1个数的所有方案都已知，且都比ii小，如果ii放在前i−1i−1个数的最左边，则会新产生i−1i−1对逆序数，如果ii放在前i−1i−1个数的最右边，则不会产生逆序数。也就是说在前i−1i−1个数已经固定，准备放置第ii个数时，可以产生的逆序数对的数量x∈[0,i−1]x∈[0,i−1]，于是有：

 

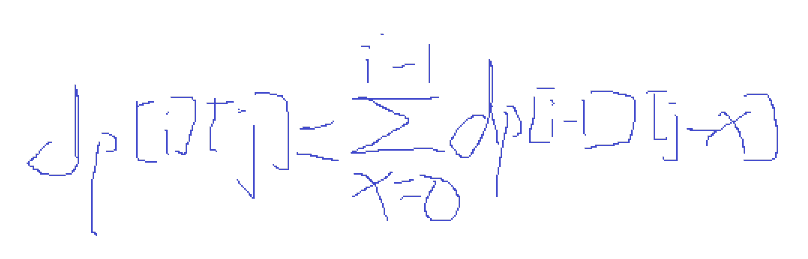
  题目只给了64MB64MB说的内存，所以需要把询问离线下来，然后用滚动数组求解同时离线答案。

参考博客：https://blog.csdn.net/xs18952904/article/details/80597966

AC代码：

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#define debug(a) cout << #a << " " << a << endl
using namespace std;
const int maxn = 5*1e3;
const int mod = 1e9 + 7;
typedef long long ll;
ll dp[3][maxn+10], ans[maxn+10], cnt = 0, cur = 0;
struct node {
    ll n, k, index;
};
node query[maxn+10];
bool cmp( node p, node q ) {
    return p.n < q.n;
}
int main() {
    std::ios::sync_with_stdio(false);
    while( cin >> query[cnt].n >> query[cnt].k ) {
        query[cnt].index = cnt;
        cnt ++;
    }
    sort( query, query+cnt, cmp );
    dp[0][0] = 1;
    for( ll i = 1; i <= maxn; i ++ ) {
        ll sum = 0;
        for( ll j = 0; j <= maxn; j ++ ) {
            sum = ( sum + dp[i-1&1][j] ) % mod;
            if( j-i >= 0 ) {
                sum = ( sum - dp[i-1&1][j-i] + mod ) % mod;
            }
            dp[i&1][j] = sum;
        }
        while( cur < cnt && query[cur].n == i ) {
            ans[query[cur].index] = dp[i&1][query[cur].k];
            cur ++;
        }
    }
    for( ll i = 0; i < cnt; i ++ ) {
        cout << ans[i] << endl;
    }
    return 0;
}

　　

最后贴一下关于滚动数组的知识：

滚动数组的作用在于优化空间，主要应用在递推或动态规划中（如01背包问题）。因为DP题目是一个自底向上的扩展过程，我们常常需要用到的是连续的解，前面的解往往可以舍去。所以用滚动数组优化是很有效的。利用滚动数组的话在N很大的情况下可以达到压缩存储的作用。

一个简单的例子：

斐波那契数列：

int main()
{
    int i;
    long long d[80];
    d[0] = 1;
    d[1] = 1;
    for(i = 2; i < 80; i++)
    {
        d[i] = d[i - 1] + d[i - 2];
    }
    printf("%lld\n",d[79]);
    return 0;
}

　　

上面这个循环d[i]只依赖于前两个数据d[i - 1]和d[i - 2]; 为了节约空间用滚动数组的做法。

int Fib[3];  

int fib(int n)
{
    Fib[1] = 0;
    Fib[2] = 1;
    for(int i = 2; i <= n; ++i)
    {
        Fib[0] = Fib[1];
       Fib[1] = Fib[2];
        Fib[2] = Fib[0] + Fib[1];
    }
    return Fib[2];
}

　　

同

int main()
{
    int i;
    long long d[3];
    d[0] = 1;
    d[1] = 1;
    for(i = 2; i < 80; i++)
    {
        d[i % 3] = d[(i - 1) % 3] + d[(i - 2) % 3];
    }
    printf("%lld\n", d[79%3]);
    return 0;
}

　　

上面的取余运算，我们成功地只保留了需要的最后3个解，数组好象在“滚动”一样，所以叫滚动数组(对于二维也可以用)。
所以，很明显，滚动数组可以通过取余（％）来实现的，(实现一个滚动|循环)
但是这里存在一个通病，那就是时间换内存一定会牺牲时间。因此，滚动数组一般用在时间比较充裕，而内存不够的情况下。

滚动数组实际是一种节省空间的办法，时间上没啥优势，多用于DP中，举个例子吧：

一个DP，平常如果需要1000×1000的空间，其实根据DP的无后效性，可以开成2×1000，然后通过滚动，获得和1000×1000一样的效果。滚动数组常用于DP之中，在DP过程中，我们在由一个状态转向另一个状态时，很可能之前存储的某些状态信息就已经无用了，例如在01背包问题中，从理解角度讲我们应开DP[i][j]的二维数组，第一维我们存处理到第几个物品，也就是阶段了，第二维存储容量，但是我们获得DP[i],只需使用DP[i - 1]的信息，DP[i - k],k>1都成了无用空间，因此我们可以将数组开成一维就行，迭代更新数组中内容，滚动数组也是这个原理，目的也一样，不过这时候的问题常常是不可能缩成一维的了，比如一个DP[i][j]需要由DP[i - 1 ][k],DP[i - 2][k]决定，i<n，0<k<=10;n <= 100000000;显然缩不成一维,正常我们应该开一个DP[100000005][11]的数组，结果很明显，超内存，其实我们只要开DP[3][11]就够了DP[i%3][j]由DP[(i - 1)%3][k]和DP[(i - 2)%3][k]决定，空间复杂度差别巨大。

参考博客

https://www.cnblogs.com/kimsimple/p/6883871.html