牛客OI测试赛 F 子序列 组合数学 欧拉降幂公式模板

链接：https://www.nowcoder.com/acm/contest/181/F
来源：牛客网

题目描述

给出一个长度为n的序列，你需要计算出所有长度为k的子序列中，除最大最小数之外所有数的乘积相乘的结果

输入描述:

第一行一个整数T，表示数据组数。
对于每组数据，第一行两个整数N，k，含义如题所示

接下来一行N个整数，表示给出的序列

保证序列内的数互不相同

输出描述:

对于每组数据，输出一个整数表示答案，对

取模
每组数据之间以换行分割

输入例子:

3
4 3
5 3 1 4
5 4
3 7 5 2 1
10 3
100 1020 2050 102 12 235 4 57 32135 54354 

输出例子:

144
81000
521918013

-->

示例1

输入

复制

3
4 3
5 3 1 4
5 4
3 7 5 2 1
10 3
100 1020 2050 102 12 235 4 57 32135 54354 

输出

复制

144
81000
521918013

说明

第一组数据解释

所有长度为3的子序列为

最终答案为

备注:

对于

的数据：

对于

的数据：

对于

的数据：

保证序列中的元素互不相同且

，

 

 

分析：

注意：ai的指数是一个非常大的数，不能直接进行快速幂计算，得先对这个指数进行降幂

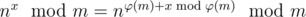　　考虑：欧拉降幂公式：，Φ(x)为欧拉函数

AC代码：

#include <map>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <bitset>
#include <cstring>
#include <iomanip>
#include <iostream>
#include <algorithm>
#define ls (r<<1)
#define rs (r<<1|1)
#define debug(a) cout << #a << " " << a << endl
using namespace std;
typedef long long ll;
const ll maxn = 1e3 + 10;
const double eps = 1e-8;
const ll mod = 1e9 + 7;
const ll inf = 1e9;
const double pi = acos(-1.0);
ll qow( ll a, ll b ) {
    ll ans = 1;
    while(b) {
        if(b&1) {
            ans = ans*a%mod;
        }
        a = a*a%mod;
        b /= 2;
    }
    return ans;
}
ll c[maxn][maxn];
//两种欧拉函数求降幂数，第一种更快点
map<ll,ll> mp;
ll phi(ll k)
{
    ll i,s=k,x=k;
    if (mp.count(k)) return mp[x];					//记忆化存储
    for(i = 2;i * i <= k; i++)
    {
        if(k % i == 0) s = s / i * (i - 1);
        while(k % i == 0) k /= i;
    }
    if(k > 1) s = s / k * (k - 1);
    mp[x]=s; return s;
}
ll eular( ll n ) {
    ll ans = n;
    for( ll i = 2; i*i <= n; i ++ ) {
        if( n%i == 0 ) {
            ans -= ans/i;
            while( n%i == 0 ) {
                n /= i;
            }
        }
    }
    if( n > 1 ) {
        ans -= ans/n;
    }
    return ans;
}
int main() {
    ll T;
    scanf("%lld",&T);
    //debug(eular(mod));   利用欧拉函数求指数循环节，这里求得的是mod-1
    memset(c,0,sizeof(c));
    c[0][0] = 1;
    for( ll i = 1; i <= 1000; i ++) {
        for( ll j = 0; j <= i; j ++) {
            if( j == 0 || j == i ) c[i][j] = 1;
            else c[i][j] = ( c[i-1][j-1] + c[i-1][j] ) % (mod-1);
        }
    }
    while( T -- ) {
        ll n, m, a[maxn];
        scanf("%lld%lld",&n,&m);
        for( ll i = 1; i <= n; i ++ ) {
            scanf("%lld",&a[i]);
        }
        sort(a+1,a+n+1);
        ll ans = 1;
        for( ll i = 1; i <= n; i ++ ) {
            ll t = ((c[n-1][m-1]-c[i-1][m-1]-c[n-i][m-1])%(mod-1)+mod-1)%(mod-1);
            ans = ans*qow(a[i],t)%mod;
        }
        printf("%lld\n",ans);
    }
    return 0;
}