R期望

斐波那契数列--九九乘法表

# 1、    打印斐波那契数列
kl<-c(1,1)
for (i in 1:8){
  kl[i+2]<-kl[i]+kl[i+1]
}
kl

# 10、    打印九九乘法表
# R 输出函数
for (i in 1:9){
  for (j in 1:i){
    cat(i,"*",j,"=",i*j," ")
  }
  cat('\n')
}

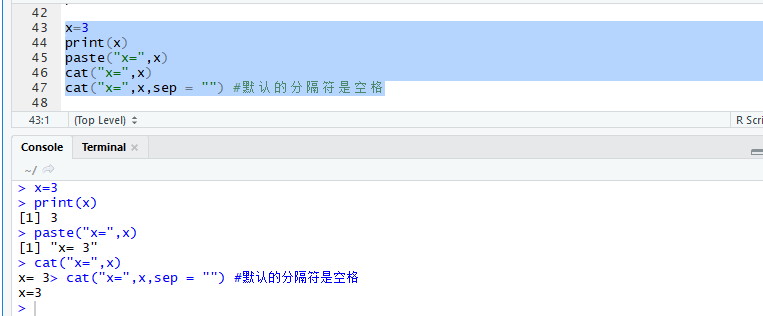
R语言的输出：cat() print() paste() 输入：scan() readline()

期望值

#一个随机事件的期望值可以看做是某种加权平均值，
#它是该事件每一个可能结果乘以权值后所得结果的总和，
#权值对应每一个可能结果出现的概率

掷一个色子

#掷一个色子
#所有结果  1   2   3   4   5   6
#所对概率 1/6 1/6 1/6 1/6 1/6 1/6
E_roll<-1*1/6+2*1/6+3*1/6+4*1/6+5*1/6+6*1/6
E_roll
# 求均值
mean(1:6)

掷两个色子

#掷两个色子
#所有结果 36
#所对概率 1/36

#列出n个向量元素的所有组合
sz<-1:6
rolls<-expand.grid(sz,sz)
#添加var1的概率
rolls$prob1<-1/6
#添加var2的概率
rolls$prob2<-1/6
rolls
#添加总概率值
rolls$prob<-rolls$prob1*rolls$prob2
#添加value值
rolls$value<-rolls$Var1+rolls$Var2
#计算期望值
E_ROLLS<-sum(rolls$prob*rolls$value)
E_ROLLS

掷两个色子（作弊）

#1 2 3 4 5的概率为1/8
#6的概率为3/8
rolls1<-expand.grid(sz,sz)
#添加var1的概率
# 1/8 5次，3/8 1次
rolls1$prob1<-rep(c(1/8,3/8),c(5,1))
#添加var2的概率
rolls1$prob2<-rep(c(1/8,1/8,1/8,1/8,1/8,3/8),each=6)
#添加总概率
rolls1$prob<-rolls1$prob1*rolls1$prob2
#添加value值
rolls1$value<-rolls1$Var1+rolls1$Var2
#计算期望值
E_ROLLS1<-sum(rolls1$prob*rolls1$value)
E_ROLLS1

构建查找表和上面一样结果

#构建查找表
prob<-c(""=1/8,""=1/8,""=1/8,
        ""=1/8,""=1/8,""=3/8)
prob[1]
# 一次看多个值
prob[c(1,2,3,4,5,6)]
unname(prob[c(1,2,3,4,5,1,2,3,4,5,6)])
#添加var1的概率
rolls1$prob1<-prob[rolls1$Var1]
#添加var2的概率
rolls1$prob2<-prob[rolls1$Var2]

计算tiger机的期望值

7*7*7
wheel<-c("DD","","BBB","BB","B","C","")
combos<-expand.grid(wheel,wheel,wheel,
                    stringsAsFactors = F)
str(combos)
#构建查找表
prob <- c("DD"=0.03,""=0.03,"BBB"=0.06,
          "BB"=0.1,"B"=0.25,"C"=0.01,""=0.52)
prob["DD"]
prob["C"]
#添加var1的概率

# prob[combos$Var1] 每个值对应的概率
combos$prob1<-unname(prob[combos$Var1])
#添加var2的概率
combos$prob2<-unname(prob[combos$Var2])
#添加var3的概率
combos$prob3<-unname(prob[combos$Var3])
#添加总概率
combos$prob<-combos$prob1*combos$prob2*combos$prob3
head(combos)
score(c("DD","DD","DD"))
#添加一列value
combos$value<-NA
combos[1,1]
combos[1,2]
combos[1,3]
c(combos[1,1],combos[1,2],combos[1,3])
score(c(combos[1,1],combos[1,2],combos[1,3]))
combos[1,"value"]<-score(c(combos[1,1],combos[1,2],combos[1,3]))
nrow(combos)
for (i in 1:343) {
  combos[i,"value"]<-score(c(combos[i,1],combos[i,2],combos[i,3]))
}
head(combos)
tail(combos)
#计算期望值
E<-sum(combos$prob*combos$value)
E

#验证期望值
sum(replicate(10,play()))
sum(replicate(100,play()))
sum(replicate(1000,play()))
sum(replicate(10000,play()))

R连接数据库

install.packages("RMySQL")
library(RMySQL)
#构造连接
conn<-dbConnect(MySQL(),user="root",
          password="",dbname="db1")
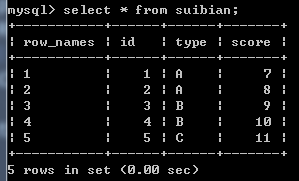
lizi<-data.frame(id=1:5,
                 type=c("A","A","B","B","C"),
                 score=7:11,
                 stringsAsFactors = F)
lizi
#把表写入数据库
dbWriteTable(conn,"suibian",lizi)
#关闭数据库
dbDisconnect(conn)

library(ggplot2)
data("diamonds",package = "ggplot2")
str(diamonds)
dbWriteTable(conn,"diamonds",diamonds,row.names=F)

Data Frame一般被翻译为数据框，感觉就像是R中的表，由行和列组成

cbind： 根据列进行合并，即叠加所有列，m列的矩阵与n列的矩阵cbind()最后变成m+n列，合并前提：cbind(a, c)中矩阵a、c的行数必需相符

rbind： 根据行进行合并，就是行的叠加，m行的矩阵与n行的矩阵rbind()最后变成m+n行，合并前提：rbind(a, c)中矩阵a、c的列数必需相符

#定义资料集
df1 = pd.DataFrame(np.ones((3,4))*0, columns=['a','b','c','d'])
df2 = pd.DataFrame(np.ones((3,4))*1, columns=['a','b','c','d'])
df3 = pd.DataFrame(np.ones((3,4))*1, columns=['a','b','c','d'])
s1 = pd.Series([1,2,3,4], index=['a','b','c','d'])

#将df2合并到df1的下面，以及重置index，并打印出结果
res = df1.append(df2, ignore_index=True)
print(res)
     a    b    c    d
0  0.0  0.0  0.0  0.0
1  0.0  0.0  0.0  0.0
2  0.0  0.0  0.0  0.0
3  1.0  1.0  1.0  1.0
4  1.0  1.0  1.0  1.0
5  1.0  1.0  1.0  1.0

#合并多个df，将df2与df3合并至df1的下面，以及重置index，并打印出结果
res = df1.append([df2, df3], ignore_index=True)

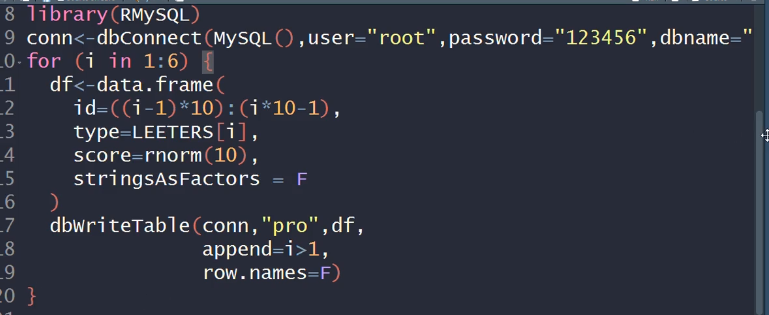
作业：构造6个数据框，每个数据框分别有三个变量，

#追加数据：append
#作业：构造6个数据框，每个数据框分别有三个变量，
#id、type、score
#id：是0-9,10-19,20-29……
#type："A","B","C"……
#score：长度为10的随机数
#把这6个数据框写到一张表里，表名：pro

install.packages("RMySQL")
library(RMySQL)
#构造连接
conn<-dbConnect(MySQL(),user="root",
                password="",dbname="db1")

a1<-data.frame(id=0:9,type=LETTERS[1:10],score=rnorm(10))
a2<-data.frame(id=10:19,type=LETTERS[1:10],score=rnorm(10))
a3<-data.frame(id=20:29,type=LETTERS[1:10],score=rnorm(10))
a4<-data.frame(id=30:39,type=LETTERS[1:10],score=rnorm(10))
a5<-data.frame(id=40:49,type=LETTERS[1:10],score=rnorm(10))
a6<-data.frame(id=50:59,type=LETTERS[1:10],score=rnorm(10))
s<-rbind(a1,a2,a3,a4,a5,a6)

#把表写入数据库
dbWriteTable(conn,"pro",s)
#关闭数据库
dbDisconnect(conn)

-----------

1122

#生成随机数
rnorm(10)

#查看数据库中有没有一张特定的表
dbExistsTable(conn,"diamonds")

#列出当前的数据库中有哪些表
dbListTables(conn)

#列出表中的字段
dbListFields(conn,"diamonds")

#读取表的数据
db_df<-dbReadTable(conn,"course")
db_df

提取数据到R里

#提取数据到R里
dbGetQuery()

#查看数据集的摘要统计量
summary(diamonds)

#1.查询cut切工的类别
dbGetQuery(conn,"select distinct cut from diamonds")

#2.查询克拉、价格、大小（size），size用x*y*z来表示
db_diamonds<-dbGetQuery(conn,"select carat,price,x*y*z as size from diamonds")
head(db_diamonds)

#3.查询克拉、切工、颜色、价格，切工是Good，颜色是E
good_e_diamonds<-dbGetQuery(conn,"select carat,cut,color,price from diamonds where cut='Good' and color='E'")
head(good_e_diamonds)

111